Построение триангуляции плоских областей методом измельчения

DOI:

Q. Треугольник T j будем называть граничным, если хотя бы две его вершины лежат на границе д Q. Остальные треугольники будем называть внутренними.

Для по с троения расчетной треугольной сетки нужно взять конечное число точек, лежащих в Q, и сформировать на их основе триангуляцию. Существует немалое количество различных алгоритмов решения этой задачи. При этом сложность этих алгоритмов в лучшем случае составляет величину O(mlnm). Существуют и другие способы построения треугольных сеток в ограниченных плоских областях. В качестве примера мы можем привести работы [1] и [10]. Мы также предлагаем несколько иной подход, предусматривающий только один проход по набору вершин. Заключ а ется он в следующем. Вначале мы рассматриваем небольшое количество точек из Q и одним из алгоритмов строим по ним начальную триангуляцию. Для получения более качественной триангуляции мы можем потребовать выполнения, например, условия Делоне или его обобщения (см., например, [4; 11; 12]). Далее построенная триангуляция подвергается процессу измельчения с целью уменьшения мелкости разбиения и, соответственно, повышению точности вычислений на ней. Отметим, что в роли числовой характеристики, отвечающей за качество триангуляции, мы рассматриваем минимальный синус углов треугольников триангуляции. Нужно отметить, что синусы углов треугольника существенно влияют на степень погрешности вычисления функции и ее производных при их приближении кусочно-полиномиальными функциями в этом треугольнике (см. работы [2; 3; 5–9; 13–15]).

Далее будем предполагать, что граница области д^ состоит из конечного числа простых замкнутых кривых. Будем считать, что задана некоторая начальная триангуляция Т = {Т ^ } ^ ₌₁ области Q. Рассмотрим следующий способ измельчения триангуляции с целью получить триангуляцию, которая будет приближать границу области с большей точностью.

Зафиксируем произвольное натуральное число q.

• 1)    Для каждого внутреннего треугольника Т _к исходной триангуляции будем строить разбиение следующим образом. Выберем произвольно вершину треугольника и каждую сторону, выходящую из этой вершины, разобьем дополнительными точками на q равных отрезков. Далее проведем через выделенные точки прямые, параллельные второй стороне, которая также выходит из данной вершины. Если теперь провести прямые, параллельные третьей стороне через полученные точки, то образуется разбиение треугольника Т _к на q ² подобных треугольников (см. рис. 1). При этом величина минимального угла полученной триангуляции совпадает с а ( Т ).

• 2)    Рассмотрим произвольный треугольник Т _к с вершинами А, В и С , у которого сторона АВ является граничной. Тогда вершины А, В Е д Q. Будем предполагать, что АС U СВ С Q. На АС рассмотрим точки С = S _oo , S ₁₀ ,..., S _{q 0} = А, делящие отрезок АС на q равных отрезков. Проведем выходящие из них лучи в сторону треугольника и параллельные стороне СВ: L _o , L 1 ,..., L _q .

Обозначим через т длину максимального отрезка вида S _{i 0} M , лежащего в пересечении Q П L _i , г = 0, ...,q. Мы будем предполагать, что 0 <  т <  + ^ . Обозначим через l _i отрезок луча L i с началом в точке S _{i 0} длины т^ Разобьем 1 _г на q — г одинаковых отрезков точками S _{i 0} , S _{i 1} ,..., S _i,_{q - i} (см. рис. 2). Образуем для получившихся точек такой набор треугольников. Для г = 0, ...,q — 1 получаем AS _ij S _i,j ₊₁ S _{i +1} ,j , j = 0, ...,q — г — 1 и A ^S ij ^S i ₊i ,j - i ^S i ₊i ,j , где ^j = 1, ...,q — г - 1.

В итоге, как не трудно видеть, полученный набор треугольников также образует триангуляцию.

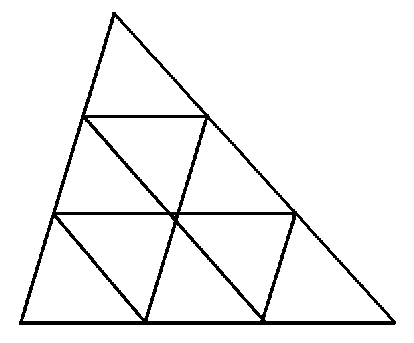
Рис. 1. Разбиение треугольника на 9 подобных треугольников ( q = 3 )

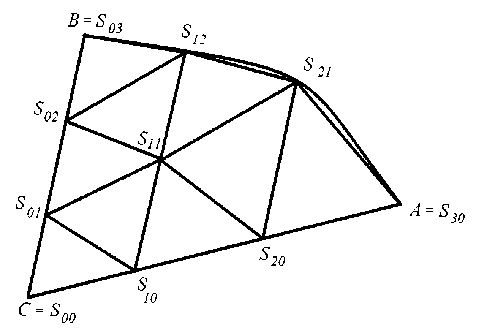
Рис. 2. Измельчение для граничного треугольника (q = 3 )

• 2.    Оценка качества триангуляции

В этом разделе статьи мы будем рассматривать область Q специального вида. Для начала дадим определение криволинейного треугольника (см. рис. 3). Пусть задана произвольная точка О = (х ₀ , у ₀ ) на плоскости и два неколлинеарных единичных вектора ^f = ( , 1 , , 2 ) и f = ( п 1 , П 2 ). Криволинейным треугольником назовем область вида

~_

Т = {М : ОМ = uf + vf, 0 < и < а, 0 < v < А(и)} или вида

• — _

Т = {М : ОМ = и, + vn, 0 < v < а, 0 < и < A(v)}, где λ — некоторая непрерывная неотрицательная функция, определенная на отрезке [0, а].

Понятно, что достаточно ограничиться первым видом криволинейного треугольника, так как треугольник второго вида приводится к первому заменой ^f на f, а f

f

f

на , . Вершинами криволинейного треугольника назовем точки О, М 1 = О + а, и М 2 = о + л <о)п.

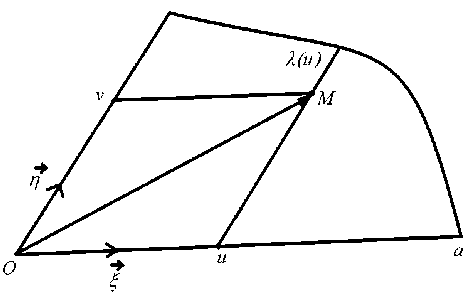
Рис. 3. Криволинейный треугольник

Пусть область Q представляет собой объединение

Q =

(У") ■• (у^т)

где Т _к — обычные (прямолинейные) треугольники, а Т _к — криволинейные треугольники. Будем предполагать, что все эти треугольники не пересекаются по внутренним точкам. Также мы будем считать, что вершины каждого треугольника (криволинейного треугольника) могут принадлежать другому треугольнику, прямолинейному или криволинейному, только в качестве его вершины (рис. 4).

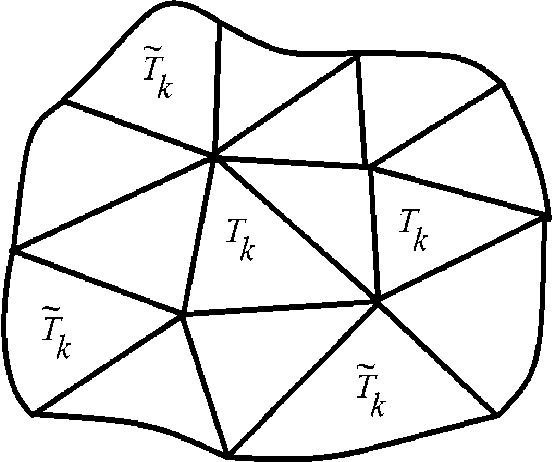
Рис. 4. Область, как объединение треугольников

Далее дадим нижнюю оценку минимального угла треугольников, получающихся описанным выше методом. Ясно, что при измельчении треугольников Т _к углы получающихся новых треугольников будут теми же, так как эти треугольники подобны треугольнику Т _к . Поэтому будем оценивать углы при измельчении криволинейных треугольников

Т _к . Для начала рассмотрим криволинейный треугольник (индекс к опустим, чтобы не загромождать формулы)

--→

Т = {М : ОМ = и^ + vq, 0 < и <  а, 0 <  v <  Л (^) } .

Будем предполагать, что найдутся положительные числа L >  Z такие, что для любых и 1 ,и ₂ £ [0, а], U 1 < и ₂ , выполнены неравенства

Z ( u - U i ) <  A (u i ) - X(U 2 ) <  L(U 2 — U i )                       (1)

и А (а) = 0. Проведем процедуру измельчения этого треугольника, описанную в предыдущем разделе статьи. Рассмотрим разбиение отрезка [0, а] точками u _i = ih, где h = ^ , г = 0,...,q. Зафиксируем i и рассмотрим точки v^ = М^-¹ , j = 0,...,q — i. Обозначим через A _ij точку с координатами ( х^,у^ ), где

Ху = Х о + U i 0 1 + V ij П 1 , У ij = У о +U i O 2 + V ij П 2 .

Отметим, что справедливы следующие неравенства

(q — i)Zh <  A (u _i ) <  (q — i)Lh, i = 0, ...,q.

Триангуляция криволинейного треугольника Т состоит из следующих треугольников. Для i = 0,..., q — 1 получаем AAyA jj +i A j +ij , j = 0,..., q — i — 1 и AA ij A i ₊i ,j _ i A i ₊i ,j , где j = 1,..., q — i — 1. Получим оценку снизу синуса углов этих треугольников.

Рассмотрим первый треугольник. Ему в координатах и, v соответствует некоторый треугольник, площадь которого в плоскости (u,v), очевидно, равна

S ‘ =

AAfUi) >  1 zh 2 .

2(q — i) - 2

Тогда, используя переход к декартовым координатам (х,у):

Х = Хо + и01 + vni, у = Уо + и^2 + vn2, площадь S треугольника AAijAi,j+1Ai+1,j будет равна

S = S ‘ sin 0 =     ^{( U i )} sin 0 >  -Zh ² sin 0 ,

2(q — i)      - 2         , где 0 — угол между векторами 0 и г|. Далее sin(ZAi+i,j) =

________ 2S ________ | ^A ij ^A i+1,j II ^A i,j+1 ^A i+1,j I

Воспользуемся следующими неравенствами. Пусть A = ( х а ,У а ),В = (х в ,У в ) — произвольные точки на плоскости. Пусть (u ^ ,v ^ ), (и _в ,v _B ) таковы, что

Х А = Х о + U _A 0 1 + V _A 4 1 , У А = У 0 + U _A 0 2 + V _A ^ 2

и

Х в = Х о + и в 0 1 + V B П 1 , У в = У о + и в О 2 + v b П 2 .

Тогда

^{( х} Л ^{- Х} в ) ^{2 + ( у} Л - У в ) ² >  (1 - | COS ^{0 | )(( и} д ^- и в ^{) 2} + ^{( х} Л ^- Х в ) ² ),          ⁽³⁾

(хЛ - Хв)2 + (уЛ - ув)2 < (1 + | cos 0|)((иЛ - ив)2 + (хЛ - Хв)2).         (4)

Поэтому

|а,, а , +„ | ² <  (1 + 1 cos 0 | ) р ■ + ( ³^ - ^-^ - 1 у)

и

I a„ +1 A , +_l, | ² <  (1 + 1 cos е | ) ( л ² + ( +   '■     - у у) .

Следовательно, sin(ZA,+1,j) >

sin 0

1 + | cos 0 1 ^^ 2 | ( ^{j A ( u} « )

KX(u , )/(q -

- ;    )² v ■

1Ж№)

9 — i

-

j^U +l ) ) 2 д — i — 1

.

Используя условия на функцию A (u), имеем

3 Ни,) 3 A(u,+1) ---- — ----- q - г q - г - 1

3 A(u,) 3 М«г+1) ---- — ----- q - г q - г

A (u , +1 ) ⁽ q ^{- г )(} q ^{- г -} 1)

Lhy Lhy

< ---- ; |--; <  2Lh

и	(з + 1) Л (и , )     3 Х(и ,+1 )		⃒⃒ ≤	3 ^ (u , )	3 A ( u i +1 )	+	A (u , )	+
	q - г       q	- г - 1		q - г	q - г		q - г
	+	3 A ( u i +1 ) ( q - г )( q - г - 1)			< 3LЛ.

Таким образом,

• , , л х         ^{sin 0                     ;Л} 2

sinlZAji I J > -----.------г ,               „         = v     1,35 ~ 1 + | cos 0| Vл2 + 4L2Л2 Vл2 + 9L2Л2

sin 0                 / = ------,--------r ,         - ,        =.                                   (5) 1 + | cos 0 | V1 + 4L2v 1 + 9L2

Аналогично имеем

Поэтому,

sin(ZAti) >     s ‘ n 0 ,                           ------------= 1 + | cos 0 | ф12 + (г^ -       ■ ) 2 A (u , )/(q - г) sin 0                 л 1 + | cos 0 | ^ Л 2 + ( Mu t ) - jA C u i +i ) ) 2 . , , . x           sin 0               I sin(^A„) >  1 + | cos e |v T+4l 2 '                         (6)

И для третьего угла данного треугольника sin 0                    hA(ui)/(q — г)

¹ + I cos ^{0 |} A ( _Mi )/(q — i) J h ² + ( (^^ — ^' ^:± ) ²

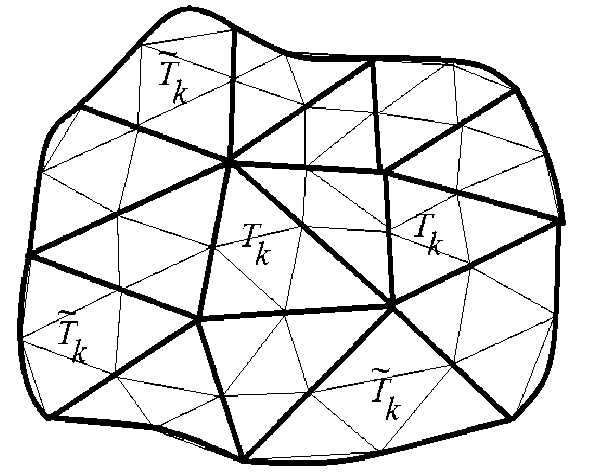
Рис. 5. Триангуляция области после измельчения для q = 2

sm( Z A i ±ij ) >

	sin 0                   h 1 + | COs 0 | ^ H ? + ( ( 2 ±1M ^ 1 ) - M^ ±1 ) ) 2
Тогда	sin 0           l sin(    M+1 ) >  1 + | cos 0 IV 1 + 9L 2 .                       ()
Аналогичные	неравенства (5)–(7) справедливы и для углов треугольника

AA _tj A _{i +1} ,j _₁ A _{i +1} ,j . На рисунке 5 показан результат измельчения исходной триангуляции.

Обозначим теперь через 0 минимальный угол всех треугольников T _k . Далее для каждого треугольника определены соответствующие постоянные I k ,L _k . Полагаем

Замечание 1. Условия (1) существенно влияют на качество триангуляции. Убедимся в этом на следующем примере. Пусть fi — круг, ограниченный окружностью ж ² + у ² = R ² . Разобьем его на четыре криволинейных треугольника координатными линиями. Пусть первый из них имеет вид

Т = { (ж, у) : 0 <  ж <  R, 0 <  у <  VR ² - ж ² } .

Ясно, что функция Л (ж) = VR2 — ж ² не удовлетворяет условиям (1). Теперь рассмотрим соответствующее измельчение и самый крайний справа треугольник АА ₀ ,_ц _ ₁ А ₁ ,_ц _ ₁ А ₀ ,,_? . Не сложно видеть, что

Л о ,, - 1 = ( я^{1 - 1} , 0 ) , а^ - = ( я^{1 - 1} ,R ^ 2^) , А о ,, = (R, 0).

Тогда

R/q

sin ⁽ Z A o ,₉ - i A i ,₉ - i A o ,y ) =

^ 0

.

при q ^ то

Замечание 2. Дадим некоторые пояснения по поводу вычисления величин г _г = Л (и _г ). Предположим вначале, что область задана неравенством

F(ж,у) < ° где F(ж, у) — непрерывная функция на плоскости. В таком случае вычисление значений гг, а значит и вершин триангуляции, может быть осуществлено так. Пусть фиксирована точка Аг0, г = 0, ..,q. Рассмотрим функцию

/ (t) = F (ж г о + t n i , у го + ^ Л 2 )

при t Е [0, + то ). Так как точка А _{г 0} Е fi, то либо /(0) = 0, либо /(0) < 0. Если /(0) = 0, то полагаем г _г = 0. Если же /(0) < 0, то, учитывая, что /(t) > 0 при всех достаточно больших t >  0, из непрерывности функции /(t) следует существование такого минимального t * >  0, что /(t * ) = 0. Тогда полагаем г _г = t * . Величину t * можно приближенно определить одним из методов численного решения нелинейных уравнений.

Предположим теперь, что граница области дfi задана в виде параметрических уравнений ж = ж(t), у = у(t), t Е [0,Т].                                 (8)

Рассмотрим криволинейный треугольник

--→

Т = {М : ОМ = иЕ, + vq, 0 < и < а, 0 < v < Л(^)}, в котором функция Л(и) задана параметрически уравнениями (8) при t Е [t1,t2] С [0,Т]. Тогда для поиска точки пересечения Lt с дfi надо решить уравнение

(у(t) — у о — и г Е 2 ) П 1 = (ж(t) — ж о — и г Е 1 ) П 2 .                       (9)

Учитывая, что x(t i ) = ж о + A (0) n i , y(t i ) = у о + Л (0) п 2 и ^(^ 2 ) = Х о + aU,y(t2) = = у ₀ + а^ ₂ и непрерывность функций x(t),y(t), найдется t * Е [t 1 ,t ₂ ] такое, при котором выполняется равенство (9). Тогда полагаем

T = У(ж ^ о - x(t * )) ² - (ую - y(t * ) ² .