Поток электромагнитной энергии в проводнике с постоянным током

Доказывается (в рамках клссической электродинамики), что поток электроэнергии в проводнике

• •    направлен вдоль оси провода,

• •    распространяется вдоль оси провода,

• •    распространяется внутри провода,

• •    компенсирует тепловые потери.

Поток электромагнитной энергии распространяется в проводе, возбуждая электрический ток. При этом передний фронт распространяющегося тока создает поток электромагнитной энергии, который возбуждает следующий элемент тока и т.д.

Оглавление

• 1.    Вступление

• 2.    Элементарные токи в проводе

• 3.    Потоки энергии в проводе

• 4.    Обсуждение Литература

2.    Элементарные токи в проводе

1.    Вступление

"… наша «сумасшедшая» теория говорит, что электроны получают свою энергию, растрачиваемую ими на создание теплоты извне, от потока энергии внешнего поля внутрь провода. Интуиция нам подсказывает, что электрон пополняет свою энергию за счет «давления», которое толкает его вдоль провода, так что энергия как будто должна течь вниз (или вверх) по проводу. А вот теория утверждает, что на самом деле на электрон действует электрическое поле, создаваемое очень далекими зарядами, и электроны теряют свою энергию, расходуемую на тепло именно из этих полей. Энергия отдаленных зарядов каким-то образом растекается по большой области пространства и затем втекает внутрь провода."

Р. Фейнман [1]

Такая теория противоречит и закону сохранения энергии. Действительно, поток энергии, путешествуя в пространстве, должен 218

терять часть энергии. Однако это никак не обнаружвается ни экспериментально, ни теоретически. Но, главное, эта теория противоречит следующему эксперименту. Пусть по цетральному проводу коаксиального кабеля течет постоянный ток. Этот провод изолирован от внешнего потока энергии. Откуда же появляется поток энергии, компенсирующий тепловые потери в проводе? Очевидно, что этот поток может появиться только со стороны других элементов провода [2]. Интуиция, о которой говорит Фейнман, нас не обманывает. Автор доказывет это ниже, не выходя за рамки клссической электродинамики.

Рассмотрим вначале проводник с постоянным током. Ток J в проводе создает в теле провода магнитную индукцию B , которая действует на электроны с зарядом q_e , движущиеся со средней скоростью v в направлении, противоположном току J , силой Лоренца F , заставляя их смещаться к центру провода – см. рис. 1.

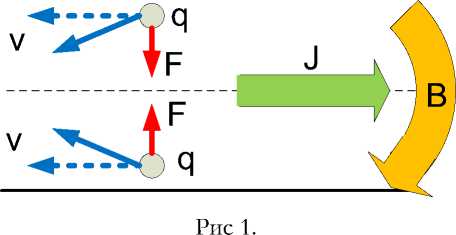
В связи с известным распределением индукции B по сечению провода сила F убывает от поверхности провода к центру – см. рис. 2, где показано изменение силы F в зависимости от радиуса r , на котором находится электрон.

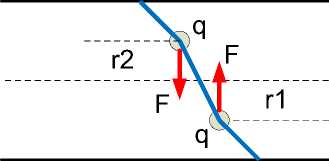
Рис 2.

Таким образом, можно полагать, что в теле провода существуют элементарные токи I , начинающиеся на оси и направленные по некоторым углом α к оси провода – см. рис. 3.

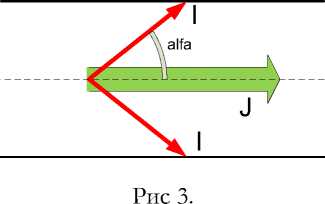
Будем полагать, что все эти токи равны по величине и эта величина не изменяется на протяжении траектории. Тогда

J = n • I cos(a)

где n – количество лементарных токов. Имеется также суммарная составляющая элементрных токов, которая направлена по радиусам от оси,

Jr = n • I sin(a)

или

Jr = J • tg(a).(1в)

Токам J и I соответствуют напряженности электрического поля вдоль траектории этих токов:

E = Jp A,(2)

e = Ip a,(3)

где ρ – удельное сопротивление; А, а - сечение провода и сечение траектории элементарного тока. Очевидно,

A - mna cos(a).

где m >  1 — некоторый коэфициент (поскольку проекции сечений а не полностью заполняют площадь А ).

Из (1-4) следует, что

ρnI cos(α) nea cos(α) nea cos(α)

E =  -----^ =-----^ «-----« —.(5)

A         A      mna cos( α ) m

3.    Потоки энергии в проводе

Магнитная напряженность H суммарного тока I и электрическая напряженность e создают поток энергии с плотностью

S i ( r ) = eH ( r ) ,                                             (6)

направленный к оси провода – см. рис. 4.

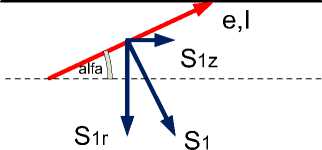
Рис 4.

Магнитная напряженность H в зависимости от радиуса r , как известно, определяется по формуле

H ( r ) = -Jr y, 2 πR ²

где R - радиус провода. Из (5-7) находим:

mEJ   mρJ ²

S ( r ) =---- rr =---- rr.

¹     2 πR ²    2 πR ²

Этот поток можно разложить на сумму потоков, направленных к радиусу и по направлению тока J , с плотностью

S 1 r ^{( r} ) = S 1 ^{( r} )cos ^{( a} ) ,                                        (9)

S 1 _z ^{( r} ) = ^S 1 ^{( r )sin ( a )} .                                         (¹⁰)

Интегрируя эти плотности, найдем полные потоки электромагнитной энергии, направленные по радиусу к оси и вдоль оси.

Поток электромагнитной энергии, направленный по радиусу к оси , находим как интеграл плотности потока (9), исходящего из трубок радиуса r с толщиной стенок dr и длиной L :

X

Sro = cos

I 2n ( R

^{1 ( a )}^ J I ^{s 1} r ■ ^rdr dp p = 0 V r = 0

= cos¹

L LmEJ

R ’ 2nR R

2 π    R

X

J J r ² drdtp =

p = 0

V r = 0

= cos¹

L LmEJ ^R ₂            LmEJ R ³

•         rdrdp = cos ( a )

R 2 πR ²                   R ³ 3

r = 0

= cos ( a ) m- LEJ

⁷ .(11)

или

Sro = kLEJ, где k = cos(a )m.

Этот поток энергии пронизывает весь объем провода по радиусу к центру. Он действует на свободные электроны провода с силой, направленной вдоль оси провода (перпендикулярно вектору потока [3]), и тем самым создает ток J .

Мощность тепловых потерь в проводе от тока J

P = LEJ .                                         (14)

Сравнивая (12) и (14) замечаем, что поток энергии (12) полностью компенсирует тепловые потери (14), если m = 3)cos(a ).                                           (15)

Поток электромагнитной энергии, направленный вдоль оси , находим как интеграл плотности (10) по площади сечения провода:

2 π   R

\

S 1 _z = sin( a ) j j S 1 _z ( r ) ■ rdrd^ = sin( a )

Ф=0 уr=0                  У mEJ R           mEJ R 3

^{sin( a} ) -Rr J r dr = ^sin ^a ) - R y- — r = 0

С учетом (1в) и (15) находим:

mEJ 2 πR ²

2 π  R

\

J j r ² drd^ =

Ф = 0 у r = 0

^У . (16)

m

= sin( a )y EJR

S_ro = sin ( a ) mm REJ r /tg( a ) = kREJ r .

Этот поток энергии пронизывает весь объем провода по оси. Он действует на свободные электроны провода с силой, направленной вдоль радиуса (перпендикулярно вектору потока [3]), и тем самым создает ток J_r - (1а), который перпендикулярен оси.

Мощность тепловых потерь в проводе от тока J_r

P_r = REJ r .                                              (18)

Сравнивая (17) и (18) замечаем, что поток энергии (17) полностью компенсирует тепловые потери (18) при условии (15). Можно заметить, что

P_r<< P .                                                 (19)

4.    Обсуждение

Ток в проводе имеет две составляющие: осевую и радиальную. Основной поток электроэнергии

• •    направлен вдоль оси провода,

• •    распространяется вдоль оси провода,

• •    распространяется внутри провода,

• •    компенсирует тепловые потери осевой составляющей тока.

Существует еще относительно слабый поток электроэнергии, который

• •    направлен вдоль перпендикулярно оси провода,

• •    распространяется вдоль оси провода,

• •    распространяется внутри провода,

• •   компенсирует тепловые потери радиальной

составляющей тока.

Тепловые потери осевой составляющей тока существенно меньше тепловых потерь радиальной составляющей тока.

Поток электромагнитной энергии распространяется в проводе, возбуждая электрический ток и компенсируя тепловые потери. При этом передний фронт распространяющегося тока создает поток электромагнитной энергии, который возбуждает следующий элемент тока и т.д.

Таким образом, ток в следующем элементе возникает как результат потока электромагнитной энергии, созданного током предыдущего элемента. Такое представление хорошо согласуется с тем известным фактом, что у молнии существует лидер, движущийся со скоростью в несколько сот километров в секунду (что было предположено автором ранее в [2]).

Предложенное доказательство можно распространить на переменные токи.