Поведение коэффициентов диффузии при посоле сельди в неподвижном тузлуке в области отрицательных температур

В общем объёме вылова порядка 8% занимает сельдь, запасы которой являются достаточными. Сельдь, как объект обработки, является классическим (традиционным) видом сырья для посола, так как она принадлежит к числу рыб, способных созревать во время посола. Этот способ консервирования не потерял актуальности и в настоящее время, когда с помощью посола получают либо готовые изделия, обладающие специфическим ароматом и вкусом, либо полуфабрикаты, из которых в дальнейшем изготавливают вяленую, копчёную, сушёную, маринованную продукцию.

Посол – сложный массообменный процесс, состоящий из диффузионного перехода соли в рыбу, диффузионно-осмотического переноса воды из тканей рыбы в тузлук и наоборот.

Движущей силой процесса посола является градиент концентрации раствора хлористого натрия как основного применяемого в промышленности консерванта, во внешней солевой среде (тузлуке) и тканях гидробионтов.

До недавних пор производство рыбы крепкого посола (свыше 12% массовой доли соли) занимало доминирующее место. В последние годы учёными установлено отрицательное воздействие на организм человека чрезмерного употребления хлористого натрия. К негативным последствиям относят: заболевания сердечнососудистой системы; повышение возбудимости центральной нервной системы, способствующей развитию гипертонической болезни; ингибирующее воздействие натрия на липопротеиновую липазу крови, уменьшающее коллоидную стабильность холестерина и являющееся одной из причин развития атеросклероза и др.

Как показали маркетинговые исследования по изучению удовлетворения потребностей населения качеством солёной рыбопродукции, гастрономические предпочтения потребителя (76%) склоняются в сторону малосолёного продукта (3–6% массовой доли соли).

С целью значительного снижения жизнедеятельности микроорганизмов и активности тканевых ферментов, а также улучшения качественных характеристик солёного продукта ряд исследователей предлагают осуществлять комбинированный посол рыбы, сочетая её обработку на отдельных этапах, как при положительных, так и отрицательных (до минус 22 °С) температурах [1, 2]. Однако эти работы посвящены установлению закономерностей при сухом посоле рыбы и не раскрывают механизм массопереноса при тузлучном (мокром) посоле.

Учитывая положительную динамику вылова сельди, её промысловый запас, благоприятное воздействие холода на подавление жизнедеятельности микроорганизмов, увеличение продолжительности хранения и улучшения качества продукта, представляется актуальным исследование и установление закономерностей процесса тузлучного посола рыбы при отрицательных температурах.

Материалы и методы исследования

В качестве объекта исследования использовали сельдь атлантическую (Clupea harengus) мороженую, по качеству отвечающую требованиям действующего стандарта размером 30 ± 2 см, массой 310 ± 10г. Химический состав мяса сельди атлантической: жир 18,5%, белок 18%, минеральные вещества 1,5%.

Для составления тузлука определенной заданной концентрации (плотности) использовали хлористый натрий по ГОСТ 4233 и воду питьевую по ГОСТ Р 51232–98.

Для исследования процесса диффузии соли в тканях сельди существующие химические способы определения солёности рыбы не позволяют получить информацию о пространственно-временном характере распределения соли в продукте. Для установления механизма распространения соли необходимо применять новые методы исследования, основанные на взаимодействиях излучений (акустических или электромагнитных) с веществом. Таким методом может быть современный оптический метод – фотонной корреляционной спектроскопии, основанный на релеевском рассеянии излучения от веществ. Учёными ФГБОУ ВО «Калининградский государственный технический университет» – Брюхановым В.В., Ивановым А.М. и др. в лаборатории микро- и нанотехнологий кафедры физики данный метод успешно применялся для исследования взаимодействия различных веществ, однако его приемлемость и целесообразность для исследования процессов пищевой технологии впервые высказана и обоснована Фатыховым Ю.А., Шума-новой М.В., Шумановым В.А. [3].

Метод фотонной корреляционной спектроскопии (ФКС) заключается в измерении коэффициента диффузии дисперсных частиц путём анализа динамических флуктуаций интенсивности рассеянного света. ФКС позволяет измерить коэффициент диффузии этих частиц и, соответственно, размер дисперсных частиц, который связан с коэффициентом диффузии [4].

Схема экспериментальной установки для исследования процесса посола мяса сельди методом фотонной корреляционной спектроскопии (ФКС) показана на (рисунок 1).

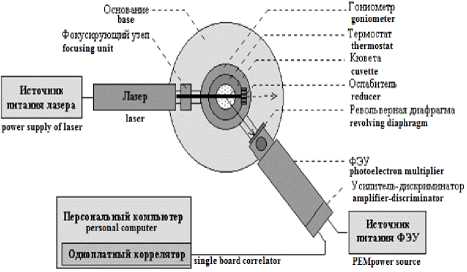
Рисунок 1. Схема экспериментальной установки

Figure 1. Diagram of the experimental facility

Она включает в себя: источник излучения, кювету с исследуемым веществом, анализатор и коррелятор, принимающие рассеянное излучение через фотоэлектронный умножитель (ФЭУ) и выводящие полученную информацию на дисплей компьютера. Источником излучения является одномодовый Не-Ne лазер (W = 15 мВт; λ = 632,8 нм; диаметр луча 100 мкм). Флуктуации интенсивности света, рассеянного на разных дисперсных частицах, регистрировались фотоэлектронным умножителем (ФЭУ), работающим в режиме счета фотонов.

Корреляционная функция вычислялась с использованием 32-битного 282-канального коррелятора «Photocor-FC», подключённого к компьютеру и снабжённого программой Flex 5.3.3. Программа рассчитывала корреляционную функцию рассеяния (временное разрешение t = 25 нс), определяла функцию распределения частиц по размерам и вычисляла коэффициент диффузии из корреляционной функции. Программа рассчитывала коэффициент диффузии с относительной погрешностью не более 5%.

Образцы сельди с кожей помещались в кювету из кварцевого стекла кожей вверх и заливались раствором NaCl заданных концентрации и температуры. Кювета помещалась в термостат, находящийся на платформе гониометра. Перемещение кюветы по высоте осуществлялось через 1 мм с помощью микрометрического устройства В каждый фиксированный момент производилось сканирование лазерным лучом тузлука, кожи и мяса сельди по высоте кюветы.

Отрицательные температуры создавались путём циркуляции тосола с жидким азотом вокруг кюветы с исследуемым образцом сельди.

Результаты и обсуждения

На рисунке 2 показано поведение коэффициента диффузии при отрицательных температурах на коже, в тузлуке, и мясе сельди. В тузлуке измерения проводились на расстоянии 1 мм от кожи, т. е. в пограничном слое, а в мясе – на расстоянии 6 мм от кожи вглубь мяса сельди.

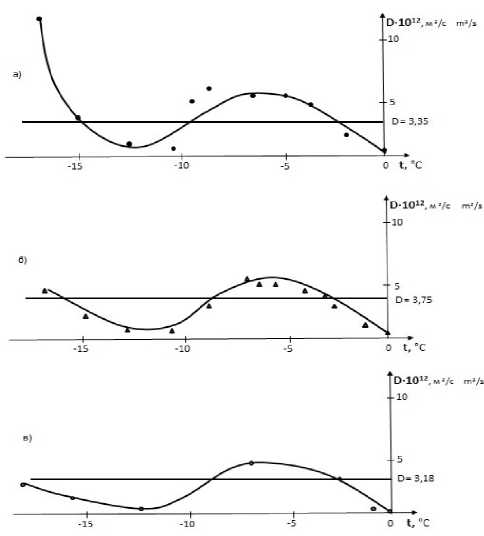
Рисунок 2. Зависимость коэффициента диффузии от температуры а) на коже; б) в тузлуке; в) в мясе

• Figure 2.    The dependence of the diffusion coefficient on temperature a) on the skin; b) in brine; c) in the meat

Как видно из рисунка 2 в исследуемых срезах образца происходят изменения коэффициентов диффузии от температуры, а изменения температуры, очевидно, связано с микроконвекцией.

На рисунке 3 представлены изменения коэффициентов диффузии по толщине исследуемого образца в кювете.

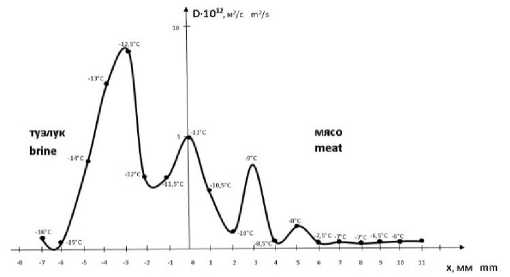
Рисунок 3. Зависимость коэффициента диффузии от расстояния в тузлуке и мясе x = 0 – кожа; x > 0 – мясо сельди; x < 0 – тузлук

• Figure 3.    The dependence of the diffusion coefficient of solution in brine and meat x = 0 – the skin; x> 0 – herring meat; x < 0 – brine

Основной движущей силой диффузионно-осмотического переноса соли и тканевой влаги рыбы является градиент концентрации. Это связано с тем, что при охлаждении образца рыбы с раствором соли до -20°С, межклеточная жидкость, находящаяся в тканях рыбы, и раствор соли не замерзают полностью. На границе раздела фаз возникают градиенты температур, связанные с термодинамическим равновесным состоянием, т.е. кристаллизацией соли и ее растворением. В результате происходит выделение и поглощение теплоты, способствующее микроконвекции.

Так как характер поведения коэффициентов диффузии, изображённый на рисунках 2 и 3 имеет качественные и количественные отличия от аналогичной зависимости при положительных температурах [5], приведём теоретические обоснования данного явления.

По мнению А.В. Лыкова [6], при малых числах Грасгофа (Gr < 50), в случае наличия источника возмущений наблюдается конвективное движение жидкости в направлении градиента возмущения за счёт молекулярной теплопроводности. Возникающие термоконвективные волны имеют вид колебательных движений при участии вязких и инерционных сил, приводящих к снижению амплитуды колебаний вплоть до полного затухания волн.

Рассмотрим подробнее механизмы

Ограничимся рассмотрением возмуще-

возникновения термоконвективных волн. Для этого принимаем следующие начальные условия осуществления процесса: насыщенный раствор NaCl с массовой концентрацией 26% при 25 °С и мясо сельди замораживаем до - 18 °С (рисунок 4).

ний малой амплитуды, что позволит пренебречь конвективными членами в (1).

Получаем линейную систему уравнений для двумерной задачи:

лазерный луч laser ray лазерный луч laser ray

насьщ енньш растворХаС! saturated solutianofNaCl

.кожа skin

^

-1

d v **

T ^d v 2* St d v *

a p       .

= —_: + V ² v *

ax ap   _*2 *

= —*- + V v2 + Gr O dx 2

—v + dx,

4=o ax 2

мясо сельди meat of herring

Рисунок 4. Схема расположения раствора и мяса сельди в кювете в исследовании процесса посола при отрицательных температурах

Figure 4. Diagram of location solution and herring meat in a cell in the study salting process at low temperatures

Предполагается, что на боковой стенке ( х 1 = 0) имеется источник периодических возмущений температуры (как и в [6]) и вертикальной составляющей скорости. Возмущения будут распространяться вдоль слоя в виде термоконвективных волн, характеристики которых определяются толщиной слоя h , свойствами жидкости, условиями на границах и величиной

5 T градиента температур у =--, где T - равно-

Эx весное распределение температур.

Будем исходить из известных уравнений естественной конвекции в приближении Буссинеска (1):

— + ( v V) v = -—V P + vV 2 9 + pOg ; ^дт             P o

— + 9V O = a V ² O ; 6т

div 9 = 0;

^{p -} P o = ^{- p} o P ^{O ;} O = T - T .

SO

St*

= ± V * ² O + v^:

Pr2

d2 , d2

где V =—■--^ - оператор Лапласа;

d x d x

B gh Y             ,        v

Gr =---2--число Грасгофа; Pr =--число v                      a

Прандтля.

Использованы следующие безразмерные величины:

x = hx * * ; x₂ = hx * ; v = —v *; P = — P

1122 _hh 2

h ²  * _Q T — T       Y *

т = —т ; O =----1; to = — rn v          Yh       h2

*

;

Далее знак «*», обозначающий безразмерные величины, будем опускать.

Таким образом, свойства термоконвективных волн в слое будут определяться безразмерными параметрами: Gr, Pr, to .

Исключая из системы (2) все неизвест-

ные, получаем уравнение для определения вертикальной компоненты скорости:

V ² [A - V ² ^fA - ± V ² ) v₂ = уд т      J\St Pr    )

S ² v₂

Gr 2

a x²

Будем искать решение уравнения (4) в виде плоских волн:

i (toT—kx v2 = V2 (x2 ) e (     *)            (5)

с амплитудой, зависящей от x .

Тогда из (4) получаем:

где — - значение плотности при постоянной

температуре T ; в = — [ — | - коэффициент

— 0 <5 ^T ) T _o

теплового расширения жидкости.

■ I 12 ^d to — i l k---

<      5 x ₂ ²

i I /2      ⁵

–    k ²–

.    a2 i k2 — IV2 = Gk2V2, (6) dx2 J

где k – волновой вектор, обезразмеренный по высоте слоя.

Решение уравнения (6) для слоя свободной верхней и твёрдой нижней (кожей) границами, на которых поддерживается постоянная температура. Равенство нулю на границах поперечной составляющей скорости V , возмущения температуры 0 и касательных напряжения ⁹ V

• ¹    учётом (2) даёт граничные условия для V : 9 X j

9V9

V2 = -2 = "XT = 0 при Х 2 = 0, h (7)

9х29х

Уравнению (6) с граничными условиями (7) удовлетворяет решение:

V = sinnx2.(8)

Напомним, что в выражении (8) V и x – безразмерные величины.

Подставляя (8) в (5), имеем:

•          i ( ют - kx )

v₂ = sinnx₂e^v       .       (9)

При избавлении от безразмерного вида:

^V . K X

V, = —sin —2 2hh

Воспользуемся данным решением. Примем случай: кювета с исследуемым образцом, охлаждённая до температуры - 18 °С, помещается на столик гониометра с более высокой температурой (комнатной плюсовой). Этим самым исключаем периодическое боковое температурное воздействие, т. е. с боков происходит стационарное воздействие среды с температурой выше, чем у образца.

Для этого примем значение частоты внешнего воздействия равным нулю, пользуясь решением (10), получаем:

2 п х ^V • ^{п х - 1}

• V, = — sin — e ' 2 _hh

Используя формулу Эйлера действительную часть, получаем: v   nx,     2 пх,

V = — sin —² cos ---¹

• ² h     h        X

  и

  
  

  .

  
  
  
  

  выделяя

  
  
  
  

Таким образом, получаем гармонические изменения вертикальной скорости в толще образца.

Расчётное максимальное значение вертикальной составляющей скорости конвективного движения при боковом температурном воздействие с нулевой частотой ( ю = 0) равно V 2 max ~ 0,3 мм\с.

Термоконвекции и образованию термоконвективных волн способствуют также химические процессы, происходящие на коже сельди (происходит диссоциация и кристаллизация). В результате этого наблюдается поглощение и выделение теплоты.

Направленность процесса и тепловой эффект определяется основным уравнением термохимии – законом Гиббса:

A G = A H - TS , (13) где A G - изменение энергии Гиббса; A H - изменение энтальпии; A S - изменение энтропии; Т – абсолютная температура.

Действительно, в уравнении (13) имеется два члена.

Для грубой оценки того, в каком направлении может протекать тот или иной процесс при низких и высоких температурах, можно воспользоваться приближенным уравнением для изменения энергии Гиббса [7-9]. При низких температурах множитель T мал и абсолютное значение произведения TS тоже мало. В этом случае для реакций, имеющих значительный тепловой эффект, |A H|» . Тогда в выражении (13) вторым членом можно пренебречь. При этом получим:

A G «А Н . (14)

При достаточно высоких температурах (множитель T велик) имеет обратное соотношение:

| A H|« . (15)

Пренебрегая теперь первым членом в выражении энергии Гиббса, получим:

A G « - TS . (16)

Эти приближенные равенства показывают, что при низких температурах критерием направления самопроизвольного протекания процесса в первом приближении может служить знак теплового эффекта, а при высоких – процесс, сопровождающийся увеличением энтропии.

Процесс выделения теплоты непосредственно вблизи границы раздела фаз способствует возникновению градиента температуры Y = д T / 9 x который изменяется внутри раствора соли от 1,0 до 0,5 °С/мм, а в межклеточном пространстве мяса сельди от 0,5 до 0 °С/мм (рисунок 3).

Диффузионно-осмотический перенос соли и тканевой влаги рыбы сопровождается малыми температурными возмущениями, вызывающими образование слабозатухающих термоконвективных волн.

В диапазоне изменения температур от - 18 °С до 0 °С была получена экспериментальная зависимость коэффициентов диффузии D в тузлуке, коже и мясе сельди от размеров диффундирующих частиц R (рисунок 5).

D ⋅ R = 242,5 ⋅ 10 ^{- 12}, (м²/с)·нм (17)

Диффундирующими частицами являются ионы Na⁺ и Cl^-, связывающие собою большое количество молекул воды H 2 O. Так из курса химии известно, что на одну молекулу NaCl приходится 400 молекул воды. Следовательно, зная коэффициент диффузии, по формуле (17) можно оценить размер диффундирующей частицы.

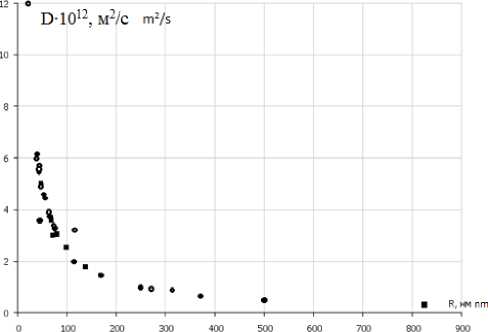
• тузлук   О кожа   ■ мясо brine skin meat

Рисунок 5. Зависимость коэффициента диффузии от размера диффундирующих частиц

• Figure 5. The dependence of the diffusion coefficient on the size of the diffusing particles

Механически разрушая диффундирующие частицы (например, с помощью акустических воздействий, т. е. звука), становится возможным увеличить значение коэффициента диффузии, тем самым ускорить продолжительность процесса посола рыбы.

Выводы

• 1.    Выявлена актуальность тузлучного посола рыбы при отрицательных температурах.

• 2.    На основе метода фотонной корреляционной спектроскопии получены волнообразные изменения коэффициентов диффузии от глубины проникновения соли в тузлуке, коже и мясе сельди, а также от температуры в диапазоне от -18 °С до 0 °С.

• 3.    На основе исследований академика А.В. Лыкова и химических процессов, происходящих на границе раздела фаз у кожи сельди, объясняется механизм образования термоконвективных волн, источником которых является температурный градиент, уменьшающийся по глубине проникновения соли. Вследствие чего термоконвективные волны слабо затухают.

• 4.    Получена зависимость коэффициентов диффузии от размеров диффундирующих частиц R:

• 5.    Для ускорения процесса посола целесообразно механическое разрушающее воздействие на диффундирующие частицы, в результате чего увеличивается коэффициент диффузии.

D ⋅ R = 242,5 ⋅ 10 ^{- 12}, (м²/с)·нм