Поведение решений системы сингулярно возмущенных дифференциальных уравнений с обобщенными неоднородными частями

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 517.928                                       

Матрица функции имеет два комплексно-сопряженных собственных значений. Неоднородная часть будет обобщенная сингулярная функция. Исследуется влияние этой функцию к явлению потери устойчивости решений.

Цель исследования: доказать асимптотическую близость решений сингулярно возмущенных дифференциальных уравнений и соответствующих невозмущенных уравнений, в случае смены устойчивости.

Материалы и методы исследования

Рассмотрим систему

£ x '( t , £ ) = D ( t ) x (tt , £ ) + £ [ ^ ( t — a ) + f ( t , x ( t , £ ) ] ,

x(t0,£) = x0(£) , ||x0(£)|| = O(£)

где 0 < £ — малый параметр, t G[t0,T] , x(t,£) = colon(xx(t,£),x2(t,£)) — искомая неизвестная функция,  S(t — a) = colon (^ (t — a), ^ (t — a))

f . t )     ⁰   1

I 0     Л ₂( t ) )

где

Л ( t ) = a (t ) + в ( t ) , Л ( t ) = a ( t ) — в (t ) .

Для решения правой части поставленной задачи (1) требуется выполнение следующих условий:

~

U1. g ( t ) , f ( t , x ) G Q ( H ) - пространство аналитических функций в области H , f ( t ,0) = 0 , | f ( t , ~) — f ( t , ~ )| <  M x |~ — ~|, 0 <  M — некоторая постоянная.

U2. Лк(t) = a(t) ±в(t), ReЛк(t) = a(t) < 0, 10 < t < T; ReЛк(T) = aT = 0, Ж) * 0,

Re Л ( t ) = a (t ) >  0 , 0 <  t <  T , к = 1,2 .

Имеет место следующая теорема:

Теорема. Пусть выполнены условия U1-U2. Тогда V t e [ t ₀, T ] решение задачи (1)-(2) существует, единственно и для него справедлива оценка

|| x(t,£ ')|| < C|xi|,                                                                      (3)

где C — const .

Доказательство. Задачу (1)–(2) заменим интегральным уравнением

Г

t

\

t

с

t

x ( t , £ ) = x °

^{( £ )ex}P ¹ j ^{D (} s ) ^{ds +} f ^exP ¹ j ^{D (} s ) ^ds '^{[d ( T —} a ) ^{+ f (} T ^{x ( т} , ^{£ ) ] d}

V

t 0

)

t 0

V

т

)

т

Для доказательства существования решения уравнения (4) применим метод последовательных приближений.

Последовательные приближения определим следующим образом:

x 0( t,£) = 0 , xn (t, £) = x 0

c

( £ )exp ¹ j D ( s ) ds + J exp ¹ j D ( s ) ds - [ ^ ( т — a ) + f (т.

V £ 10          ) 10     V £т          )

t

t

t

\

, ^x n — 1 ^{( т} , ^£ Я ^{d т} ,

V

t 0

)

t 0

V

где n g N .

t

Далее u (t, 10) = Re j D (s) ds.

t 0

Определим область H0 = {t: u(t, 10) < 0}.

Из (5) оценим последовательные приближения на замкнутой области H 0 . Тогда

x_l j( t , £ ) = x ° ( £ )exp — j 2 ( s ) ds + j 2 ( t — a )exp — j 2 ( s ) ds d r ;

V ^£ 1 0            7    1 0                   V ^£ r            7

t

t

t

v

t 0

t 0

t

t

t

\

1,,.,             1h,^l.

X 21 ( t , £ ) = x ₂ ( ^ )exp -p2 ( s ) ds +1 ^ ₂( t - a )exp - J s ) ds d r .

£                          [si

V

t

' 0

t

V

T

t

\

t

\

Отсюда имеем: x_n

1k1

(t, s) = x^£)exp -p(s)ds + exP p2(s)ds . £J£

V t о          7        V a

V

t

t

t

Здесь учтено что,

tt   t

J 2 ( t — a ) exp -p ( s ) ds d r = exp -p ( s ) ds .

t 0               V £ T         7          V £ a        7

Определим модуль решений x J t , s )| <  x 0

Будет пятеро случаи:

1). Если

t 0

< a

t

t

\

1k1k

(s)exp -\ 21 (s)ds + exp - f^,(s)ds.

££

V  t о          7        V a

V

t 0

то длину задержки решений определяет величина x 0

t

( £ ь 1 j 2 1 ( s ) ds ;

V

t 0

t

2). Если

t 0

> a

1t то длину задержки решений определяет величина exp — j21 (s)ds ;

V ^£ a        7

;

3). Если

t 0

= a

то длину задержки тоже определяет величина

^exp ¹ j ² 1 ^{( s} ) ^ds  ;

V £ a        7

г

;

4). Если a ^ ^ , то функция Дирака будет з_г ( t — a ) = 0 и длину задержки решений

t

определяет величина

x 0

( ^£ ) exp -J ² ( ^s ) ds . £!

V

t 0

t

5). Если a =

1 t

0, то длину задержки определяют величина exp —j 2 1 ( s ) ds .

V ^£ 0         7

Это означает что, в этом случае явления задержки потери устойчивости не выполняется.

Отсюда появится ограничение на постоянную a . Этот случай не будем рассматривать.

В остальном случае имеет места оценка t £ H 0 :

I x _n( t , £ )| <  C exp

u 1 ⁽ t , t 0 )

£   7

где 0 < C — const, щ (t, t0 ) = Re j 2 (s)ds • t 0

Собственные значения комплексно-сопряженные поэтому

I x₂ /t , £ )| <  C exp

u 2 ( t , 1 0 )

£

где 0 <  C - const , u 2 ( t , 1 ₀ ) = Re j Л 2 ( s ) ds .

t ₀

Если на оценку влияет величина

t

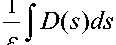
x

, оценка (6) и (7) верна на отрезки

t о ^{+ a ( s} ) <  t <  T   ^{a ( s} ) , a ( s ) — — 0 , s —— 0 и s = o ( a ( s ) ) .

Второе приближения определяется следующим образом:

t

^X 12 ( t , 8 ) = x _nC t , s ) + j f 1 ( t , x _n, x 21

t ₀

Здесь max { x (t , s ) ,1 x ₂ J t , s'

t

X

) exp ¹ j l ( s ) ds d r .

I sT        7

• )| } = М| х ц( t , s )| . Тогда

t

t

t

T

X

T

J x 11 ( t , s ) exp ¹ J l ( s)ds d r = M^ x 0 ( s ) exp ¹ j l ( s ) ds + exp ¹ j l ( ,s ) ds '0                 к ^£ T          7           t 0               I ^s t 0           7        к ^s a

t ₀

к

t ₀

к

t ₀

t

X exp ¹ j l ( s ) ds d r . к s r        7

Отсюда

t

T

x

t

m J x 0 ( s )exp — J l ( s ) ds exp — J l ( s ) ds d r = x 0

Г о           к s r         7 к s r        7

t ₀

к

t ₀

t

T

X

t

X

t

X

⁽£ ) M exp ¹ j 2 1 ( s ) ds ( t ^- 1 о ) I ^s о о           7

, а также

t

X

к

jexp ¹ j l ( s ) ds exp ¹ j l ( s ) ds d r = M exp ¹ j l ( s ) ds ( t - 1 ₀).

о о     к s a        7 к s r        7            к s a        7

t

к

к

к

Тогда | x ₁₂ ( t , s )| <  C s exp

¹ u M) Y + M ( t - 1 0 )] + M exp [ u 1M ) 1 - 1 0 ) .

к ^s

Аналогично для | x ₂₂( t , s )| <  C s exp

। u 2⁽ t , t 0 ) '

к ^£    7

t

к s 7

[ 1 + M ( t - 1 ₀)] + M exp I u 2-k,Y) к ^s 7

^{( t -} t о ) .

При n = 3 имеем x ₁₃( t , s ) = x _n ⁽ t , ^s ) ⁺ j f 1 ^{( T}, x 12 , t ₀

Отсюда max

^{ x 12 ^{( t} , ^s 11 x 22 ^{( t} , ^s )|^} = ^M| x 12 ^{( t} , ^{s )} .

Тогда x ₃( t , s )| <  C s exp I u iXkk)

к

t

X

x ₂₂)exp ¹ j l ( s ) ds d r .

к s r        7

1 + ^{M ( t -} t о ) + — ^{( t -} t о ^{) 2}

X

M ²      | u 1⁽ t , t о ) I         2.

^{+       exp} I ---------- l^{( t -} t 0 ) ;

2       к 8    )

t

Для второго собственного значения x ₂₃( t , s ) = x ₂₁ ⁽ t , ^s ) + j f 2 ^{( r} , x 1

t ₀

t

X

1г x22)exp “J^2(s)ds dT . кs r        7

12 , x 22

Здесь max

^{ x 12 ( t , ^s ), | x 22 ^{( t} , ^s )| ^} = ^M| x 12 ^{( t} , ^s )

I x _{2 3}( t , s )| <  C s exp | u ²( t ’ t ^{о )} к s

к

¹ + ^{M ( t -} t о ) +— ( t ^- t 0 ⁾²

X

M ²       u ( t , t )

+ — exp I         l ( t - 1 0 ) ,

2       к s 7

t

Аналогично x _n ⁽ t , ^s ) = ^x 11 ⁽ t , ^s ) ⁺ j f 1 ^{( r} , ^x 1 _n - 1 , ^x 2 n - 1

t ₀

t

X

^{) e}xp i s j ^{l (} s ) ds I ^{d r} .

к

T

Получим x _и( t , £ )| <  C £ exp ^f u ^{1 (} t , t ^{o )}

z

V

M    2     M

¹ + ^{M ( t -} t о ⁾⁺—-^{( t -} t о ) ⁺ ... ^{+        ( t -} t о )

2                     ( n - 1 )!

, n - 1

+

+ M       ^f u 1 ⁽ t , t — ^       ^{n - 1}

+ ( n - 1 )! ^exp V £    7^{( t}  t ⁰ )    .

Или X _и( t , £ )| <  C £ exp

U ( t , t o) ^             w M

-------  I exp ( M ⁽ t - 1 о )) +₇----v exp

V £   7                    ( n - 1 )!

^ Щ^ \ _ ^ ) n ^{- 1} .

V ^£  7

Для второго собственного значения

t x2n (t, £) = x21(t, £) + j f 2n-1 (T, x 1 n-1, X2n-1

t о

z

t

\

^)expH j Us ) ds l d T .

V

T

Получим | x _2и ( t , £ )| <  C £ exp ^f u ^{2 (} t , t ^{o )}

z

V

1 + ^{M ( t -} t о ) + — ^{( t -} t о ⁾² + ... + у--- V ^{( t -} t о )

2                     ( n - 1 )!

\

n - '

+

M^{n - 1}

+       exp

( n - 1 )!

' u^^ \ — ^ ) n ^{- 1} .

V ^£   7

Или | x_2n ( t, £ )| <  C £ exp

u 2 ⁽ t , t о ) ^

£

Докажем справедливости

z

t

t

x 1 n + 1 ⁽ t , ^£ ) = x 1⁰

exp ( M ( t - 1 ₀)) +   —у exp

оценки

z

t

^f usta X —   ) n ^{- 1}.

V ^£   7

для n +1. Тогда из (4)

\

( £ )exp 1 j Л ( s ) ds + j exp 1 j Л ( s ) ds - ^ ⁽t - a ) + f (t, V t о             7 t о       ^{V T             7}

V

о

о

имеем

, x 1 n , x 2n )^ ,

V

I ^X 1 n + 1 ⁽ t , ^{£ )}| <  C ^{£ ex} p ^f u ⁽ t , t ^о) ^ ^ex p ^{( M ( t -} t о )) ⁺ M - ^ex p ^f ^^\t ^- t о ) n .

V £    7                       n !       V £   )

Для ^X 2 n + 1

⁽ t , ^£ ) = ^X 2^о

V

|^X 2 n + 1 ⁽ t , ^£ )| <  ^{C £} exp

u 2 ⁽ t , t о ) '

^£   7

V

t

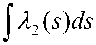
', ^x 1 n

, ^X 2 n ^{) ] d T} ,

exp ( M ( t - 1 _о )) + M — exp ^f u ^{2 (} t , a ) n !      V £   7

^{( t -} t о ) n .

Последовательные приближения равномерно ограничены: V n e N : || ^X n ⁽ t , ^£ )|| <  ^C|^X J .

Докажем

сходимости

{ ^X n ⁽ t , ^{£ ) }}

X n ( t , £ ) = X 1 ( t , £ ) + ( X 2 ( t , £ ) - X 1 ( t , £ ) ) + ( X ₃ ( t , £ ) - X 2 ( t , £ ) ) + ... + ( X n ( t , £ ) - X n₄

t

(4)^ Xn(t,£) - Xn-1(t,£) = j exp t о

t

\

¹ j Л ^(s)^ds [ ^{f (} T ^X n -Д т ^£ )) ^{- f} (

V £t        7

T , X n _₂( t , £ ) ) ] d T .

Тогда

||X j ( t , £ ) - X _o ( t , £ ) )| <  C|X j I

I X 2 ( t , £ ) - X 1 ( t , £ ) )| < C ²1 x J

... , ... , ... ,

||Xn (t,£)- xn-1 (t, £))|< Cn|x1| .

IX1 (t, £) + (X 2 (t, £)- X1 (t, £))+ ... + (xn (t, £)- Xn-i (t, f)]| < ||x (t, £ ))| +

+ ||X2 (t,£)- X(t, £| + ... + ||Xn (t,£)- Xn-1 (t,£}|| < |X11(1 + C + C2 + ... + C" 1).

Правая часть равенство (8): || x_n ( t , £ )| <

I X i l⁽¹ - C " ⁺¹ I

1 - C

при

n ^ да имеем

IX (t,£ )|<

IX1I 1 - C

< C\X 1|

Методом от противного докажем единственности решения. Пусть существует другое решения задачи (4):

t

к

t

c

t

к

xn

y ( t , £ ): y ( t , £ ) = X⁰

( £ )exp ¹ J D ( s ) ds + j exp ¹ j D ( s ) ds -\д( т - a ) + f ( t , y ( t , £ )) ] d к ^£ 1 0           J 1 0      V ^£ t          J

V

t 0

)

t 0

t

.

t (1 t

(I,£) - y(t,£)=j exp I-j D(s)ds l\f(

t

t

к

^t , ^X n - 1 ^{( t} , ^£ ) ^- f ^{( t} , y ^{( t} , ^{£ ) ]} d ^T ,

t

' 0

к

t

J

t            I t

здесь Xn(t,£) = X1( t,£) + j exp -j D(s) ds f (т,X"-10,£))dT.

t

/

t

t 0

' 0

к

t

J

Тогда

t

t

к

t            I                   t

IIX1(t,£)-y(t,£)< fexP -RejD(s)ds 'I|X00£)-y0£)))dT < C|X1|, £

t f

' 0

к

t

J

t            I                   t

||X2 (t,£)- y(t,£)|

t

t

\

t 0

' 0

к

t

J

t

t

t            I                  t

II Xn (t, £)- y (t, 4< fexP -Ref D(s ) ds 'I |Xn -1 0 £)- y(t, £ )|dT < C"|X1| . £

t

’ 0

к

t

j

Здесь выполняется Vn e N (9). Тогда в области H0:

limc"|x = 0 .

n ^^

Из равенства (9) при n^/..> ||x(t,£)-y(t,£)| < 0. Отсюда x(t,e)=y(t,s). Теорема доказана.

Пример. λ1(t)=t+i, λ2(t)=t-i, δ(t-a), a>0. Тогда условия U2 выполняется и для решения задачи (1)–(2) верно оценка (3).

Результаты и обсуждение

Если неоднородность это сингулярные обобщенные функции, то имеет место явление затягивания потери устойчивости. Функции Дирака не являются функциями в обычном смысле. Поэтому в выше полученных оценках, оценка решений задачи (1)-(2) зависит точкой . Оценка решений получается в действительной области.

Выводы

Если неоднородность будет функциями в обычном смысле, такие случаи исследованы в работах [1-3]. В противном случае оценка решений зависит от точки сингулярной обобщенной функции Дирака.