Поверхностные поляритоны на границе нанокомпозита

Нанокомпозитные материалы в последнее время привлекают внимание многих исследователей. Причина заключается в возможности эффективного управления свойствами материала. В этом контексте исследование характера поверхностных поляритонов и поверхностных плазмонов для нанокомпозитных материалов представляет не только научный, но и прикладной аспекты. Поверхностные поляритоны и плазмоны могут возбуждаться в метаматериалах, исследование которых составляет в настоящее время особое направление в радиофизике и физике конденсированных сред [2–5].

В настоящей работе мы проведем анализ свойств поверхностных поляритонов на границе нанокомпозита, образованного наночастицами из резонансного полупроводникового материала в диэлектрической матрице.

Как известно [1], поверхностные поляритоны могут возбуждаться на границе изотропного материала в случае, когда благодаря частотной дисперсии диэлектрическая проницаемость материала принимает отрицательные значения.

Рассмотрим случай, когда диэлектрическая проницаемость наночастиц композита имеет резонансный характер и имеет вид

Ω - ω - iωΓ 22   ,

Ω⊥ - ω - iωΓ

ε(ω) =ε

здесь ω – частота электромагнитной волны; Ω , Ω _⊥ – соответственно продольная и поперечная частоты частицы; Γ – параметр затуха-

ния; ε_∞

–

диэлектрическая проницаемость при

ω→∞ . При ω→ 0 диэлектрическая проницаемость принимает значение

Q 2

ε0 =ε∞    .

Ω2⊥

Отсюда можно получить значение Ω по известным Ω _⊥ , ε ₀, ε_∞ . Расчеты харакеристик поверхностных поляритонов проводились при следующих значениях параметров Ω _⊥ = 500 см ^{- 1}, ε ₀ = 5, ε_∞ = 2, Γ= 10 см ^{- 1}.

В случае композитного материала диэлектрическая проницаемость нанокомпозита будем вычислять с помощью модели Максвелла – Гарнета

ε mix

-

εd

ε _mix + 2 ε _d Здесь f – композите;

=f ε(ω)-εd ε(ω)+2εd .

относительный объем наночастиц в

εd

–

диэлектрическая проницае-

мость матрицы композита. Для расчета использованы следующие значения параметров f = 0.8, ε _d = 2.56.

Из формулы (1) можно найти диэлектрическую проницаемость нанокомпозитного материала

β 1 ε + 2 β 0 ε d ε mix =ε d

β0ε + β2εd

Здесь

.

β 0 = 1 - f , β 1 = 1 + 2 f , β 2 = 2 + f .

На рис. 1 показаны графики действительных и мнимых частей диэлектрической проницаемости для наночастиц исходного материала. Отрицательные значения действительной части диэ-

Рис. 1

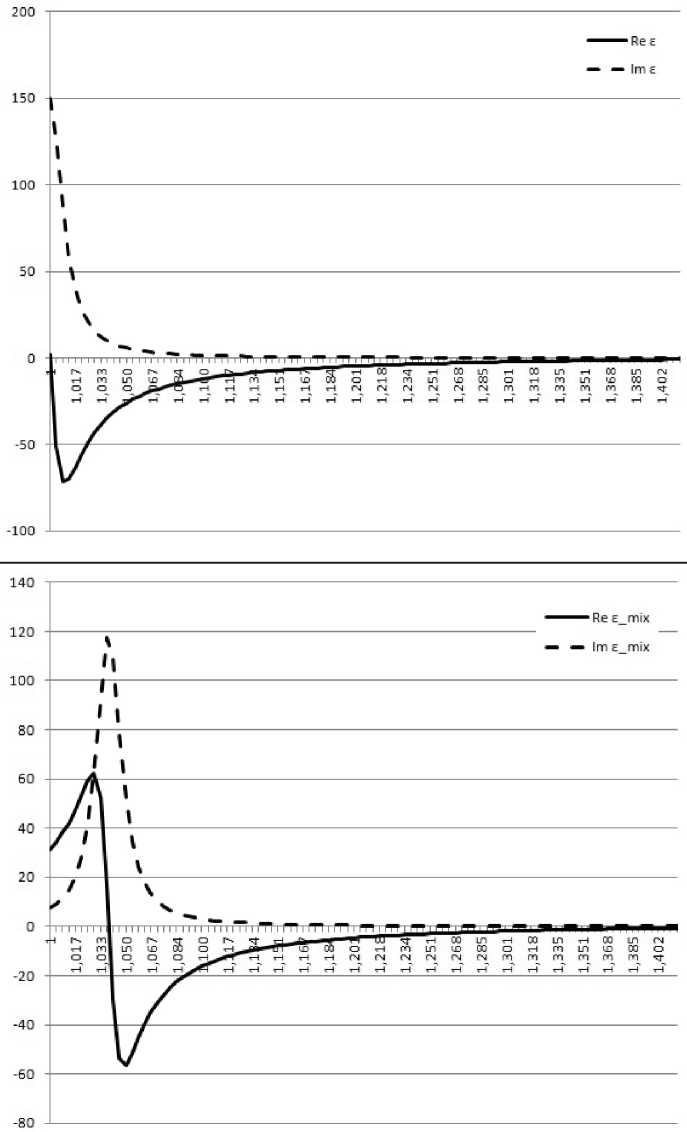
Рис. 2

лектрической проницаемости отвечают области возбуждения поверхностных поляритонов. На этих и последующих частотных зависимостях по оси абсцисс показана относительная частота y = to / Q_± .

На рис. 2 показаны частотные зависимости действительной и мнимой частей диэлектрической проницаемости всего нанокомпозита.

Сравнивая графики на обоих рисунках мы видим, что области частот, где действительная часть диэлектрической проницаемости отрицательна, отличаются для случая чистого полупроводника и нанокомпозита.

Нами проведен анализ дисперсионных кривых для нанокомпозита. Дисперсионное уравнение для поверхностных поляритонов на границе диэлектрик-изотропный резонансный материала имеет следующий вид n 2 =

^S 1 ^S mix

^S 1 + ^s mix

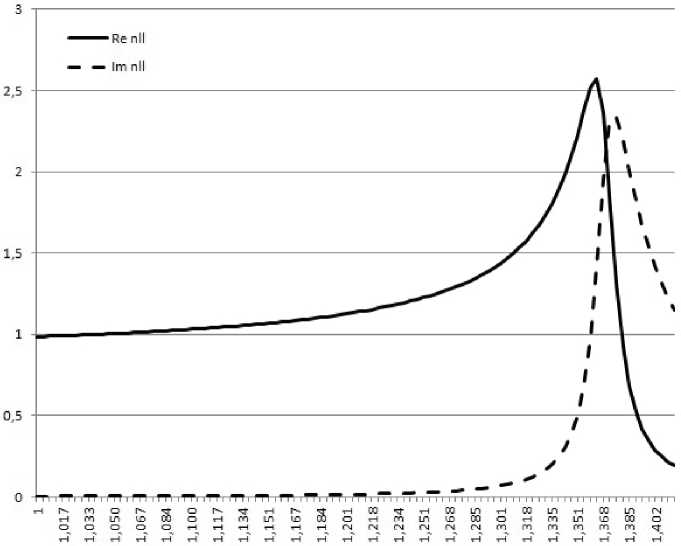
Рис. 3

Рис. 4

Здесь П ц = е^ / to ; c — скорость света; k — волновое число поверхностного поляритона.

На рис. 5 изображены графики зависимостей действительной и мнимой частей параллельной составляющей волнового вектора поверхностного поляритона от частоты.

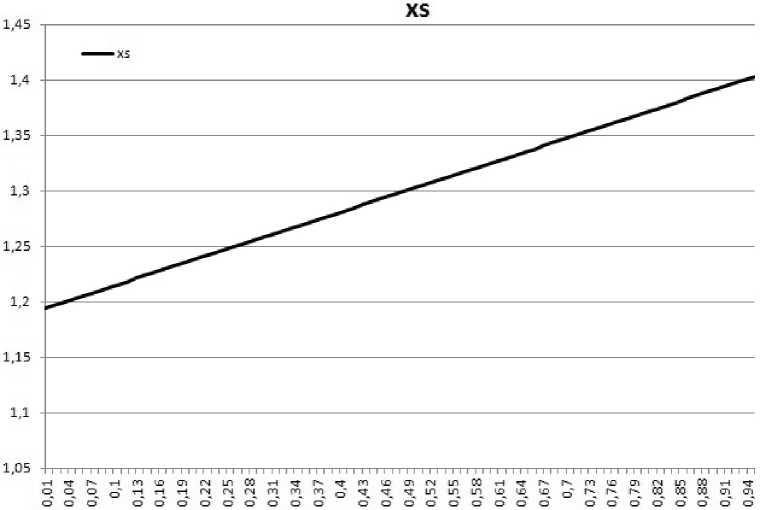
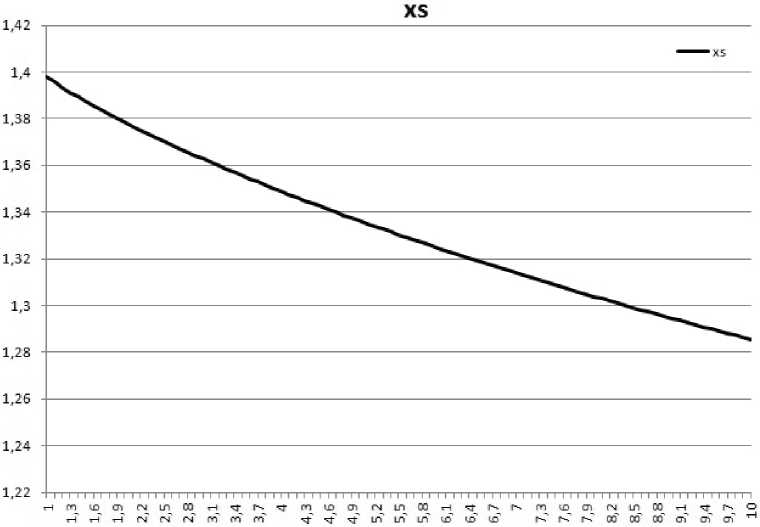
Мы провели анализ зависимости относительной частоты поверхностного поляритона от объемной концентрации наночастиц f, а также от значения диэлектрической проницаемости б d матрицы нанокомпозита. Зависимость от концентрации показана на рис. 4. Видно, что с уве- личением концентрации частота поверхностного поляритона в нанокомпозите растет. В частотном спектре постоянной распространения поверхностного поляритона это приводит к смещению максимума постоянной распространения в сторону увеличения частоты. На рис. 5 показана зависимость частоты частоты поверхностного поляритона от значения диэлектрической проницаемости матрицы нанокомпозита. В этом случае частота поверхностного поляритона уменьшается с ростом диэлектрической проницаемости матрицы нанокомпозита.

Рис. 5

Анализ проведенный в данной работе показывает на широкие возможности управления параметрами поверхностных поляритонов в нанокомпозитах из полупроводниковых наночастиц в диэлектрической матрице.