Повышение информативности систем радиолокации на основе решения вариационных задач

Актуальной задачей радиолокации является обнаружение, идентификация и измерение координат малозаметных радиолокационных целей, особенно целей, защищённых сверхширокополосными радиопоглощающими покрытиями. Один из предложенных путей решения – использование в качестве зондирующих сигналов

ВЕСТНИК 2015

сверхширокополосных (СШП) импульсов с длительностью порядка наносекунды.

Повышение информативности РЛС при использовании сигналов со сверхширокой полосой частот в значительной степени происходит благодаря увеличению разрешающей способности по дальности, а также за счёт раздельного приёма отражённых импульсов от различных фрагментов исследуемых объектов. При длительности излучаемого импульса в 1 нс разрешение по дальности составляет 30 см. Принимаемые сигналы несут информацию не только о цели в целом, но и об ее отдельных элементах, что позволяет провести распознавание класса и типа цели, а также получить её радиоизображение. Перспективным является исследование зависимости формы принимаемых сигналов от частотной зависимости эффективной площади рассеяния (ЭПР) объектов, что позволит увеличить вероятность правильной идентификации объектов.

Обнаружение целей, защищённых сверхширокополосными радиопоглощающими покрытиями, становится возможным за счёт включения в состав импульсов низкочастотных составляющих, которые относительно слабо поглощаются покрытиями. Увеличение доли низкочастотных составляющих в спектре резко улучшает характеристики обнаружения, но при этом возрастает ширина диаграммы направленности (ДН), что приводит к снижению точности угловых измерений и угловой разрешающей способности РЛС [1].

Возникает практически важная задача формирования зондирующих импульсов с максимально возможно содержанием низкочастотных составляющих при дополнительном ограничении: ширина получающейся ДН должна позволять проводить измерения угловых координат объектов с необходимой точностью.

Постановка задачи . В работах [2–5] поставлены и решены частные задачи оптимизации формы амплитудного и фазового спектров СШП импульсов на основе полных или частичных данных об отражающих свойствах целей. Значения наибольшей ω _max и наименьшей ω _min частот, входящих в спектр СШП импульсов, считались фиксированными.

Было показано, что, адаптируя спектральный состав СШП импульсов к характеристикам отражения цели и дисперсионным свойствам приёмо-передающей антенны, можно без снижения точности угловых измерений резко увеличить максимальное значение принимаемого отражённого сигнала, т.е. увеличить дальность действия РЛС.

Рассмотрим общую задачу увеличения дальности обнаружения малозаметных целей на основе оптимизации спектра (формы) зондирующих СШП импульсов при заданной точности угловых измерений, определяемой шириной ДН.

Пусть функция Ur(t) описывает зависимость от времени принимаемого импульса. Одним из важнейших параметров обнаружения импульса является максимальное (пиковое) значение сиг- нала:

U M = maX( U r ( t ))•                         (1)

Требуется найти спектральный состав генерируемого СШП импульса, включая значения наибольшей и наименьшей частот спектра ω _max и ω _min, обеспечивающий максимальное значение (1) среди всех возможных реализаций U _r( 0 , t ) при дополнительных условиях:

• 1)    ширина полученной ДН не должна превышать заданную ширину θ _0,5;

• 2)    для корректного сравнения получаемых решений энергия всех исследуемых типов импульсов должна быть одинаковой, т.е.

^τ ∫ U ²( t ) dt = ^m ∫ ^ax V ( ω ) V ^*( ω ) d ω = const. (2)

0                 ω min

Введены обозначения: U ( t ) – временная зависимость генерируемого СШП импульса, τ – его длительность, V ( ω ) – подлежащий определению комплексный спектр генерируемого импульса, V *( ω ) – комплексно сопряжённая функция.

Решение. Для упрощения получаемых в дальнейшем выражений будем считать форму ДН на каждой частоте рассматриваемого диапазона игольчатой, симметричной по углу отно- сительно направления на максимум и описывать только с помощью угла отклонения от максимума θ.

Нормированные на коэффициент направленного действия (КНД) на каждой из используемых частот ДН антенной системы обозначим f ( θ , ω ).

Комплексный спектр, а следовательно, и форма СШП импульсов, претерпевают значительные изменения при излучении, отражении от объекта и приёме сигнала [3; 4].

Спектр импульса, излучаемого в направлении θ :

V_e ( θ , ω ) = V ( ω ) f ( θ , ω ), (3) спектр сигнала, отражённого в обратном направлении на РЛС:

V_R ( θ , ω ) = V_e ( ω ) R ( ω ), (4) спектр импульса, принимаемого с направления θ :

Vr(θ,ω) = VR(ω) fr(θ,ω), (5) где R(ω) – заданная комплексная функция, опи- сывающая частотные характеристики отражения объекта, которую назовём коэффициентом отражения объекта. Зависимость функции R от частоты представим в виде:

R ( m ) = 7 ^ ( ^ )exp( i ф ( ю ))^{, (6)} где σ ( ω ) – частотная зависимость эффективной площади рассеяния (ЭПР) цели; φ ( ω ) – фазо-

ти спектр генерируемого сигнала V ( ω ), включая значения ω _max и ω _min, обеспечивающий при θ = 0 максимум функционала (7) по заданным частотным зависимостям ДН f ( го, 9 ) и характеристикам отражения цели в виде комплексной функции R ( ω ) с дополнительными условиями (2) и (9).

Решение задачи разделим на два этапа. На

частотная характеристика отражения.

Временные зависимости СШП импульсов получим, выполнив преобразование Фурье комп-

первом строится алгоритм поиска спектра генерируемого сигнала V ( ω ) для задаваемых фиксированных значений ω _max и ω _min. На втором этапе

лексных спектров.

В итоге, максимальное значение сигнала, принимаемого с направления θ , может быть

представлено как:

Um (9) = max(Ur (9, t)) = t mmax

A

= max

t

J V( m )f e ( 9 ,ю)R( to )f r ( 9 , to) exp(i m t ) d m .

v ^m min

проводится сравнение полученных результатов, и из рассмотренного множества [ to min , to max ] определяются значения наибольшей и наименьшей частот и соответствующий им спектр СШП импульсов V ( ω ), обеспечивающий максимально возможное значение U_M(0) из (7).

Первый этап сводится к решению вариационной задачи поиска спектра V ( ω ), при котором достигается максимум функционала (7) при дополнительных условиях (2, 9) для фиксирован-

Полуширину ДН при приёме СШП импульсов определим по уровню снижения максимума сигнала в 2 раз и зададим в виде угла θ ₀, так что θ ₀₅ = 2 θ ₀. В этом случае максимальные значения СШП импульсов для углов прихода сигнала θ = 0 и θ = θ ₀ связаны соотношением:

U_M ( θ ₀) = 2 /2 U_M (0). (8)

Из (3–8), в частности, следует, что ширина ДН при использовании СШП импульсов оказывается различной при излучении и при приёме сигналов. Ширина и форма ДН определяются не только частотными свойствами антенны, но также шириной и формой спектра СШП импульсов и, кроме того, частотной зависимостью коэффициента отражения цели R ( ω ).

Используя (7, 8), представим первое дополнительное условие поставленной задачи в формализованном виде:

ных значений ω _max и ω _min .

Введя неопределённые множители Лагранжа λ ₁ и λ ₂, приходим к системе уравнений:

R( ® ) f ² (0, ® )exp( i ro t ₀) - X 1 R ( ® ) { f ² (0, ® )exp( i m t ₀) - 2ff¹ ( 9 0 , ro )exp( ro t ! ) }

= ^ 2 V * ГО ) -

-

^m max

< J V ( ю ) f 2 (0, го) R ( m )exp( i m t ₀) d m _b ^m mm

2 =

= m f a V ( m ) f 2( 9₀,to )R ( m )exp( i m t 1 ) d m .      (11)

^m min

^ max

J V( ro )V*( ro )d ro = 1 , , ^ min

p>      mmax

---max( J V(to)fe(0, ю)R(to)fr (0, m) exp(imt)dm) = 2t mmin tomax

= max( J V( to )f_e( 0 _o, to )R( to )f_r( 0 _O, to )exp( i m t ) d m ) .

t tomin

Характеристики отражения в виде R ( ω ) при решении задачи считаются известными, что предполагает использование предварительной информации о радиолокационной цели. При отсутствии такой информации следует иcпользовать какую-либо математическую модель частотной зависимости ЭПР малозаметной цели.

Таким образом, приходим к математической формулировке поставленной задачи: най-

где t ₀ и t ₁ – время прихода максимумов СШП импульсов, принимаемых с направлений θ = 0 и θ = θ ₀. В общем случае значения t ₀ и t ₁ могут различаться.

Спектр V ( ω ) определяется с точностью до постоянного множителя, поэтому в последнем уравнении (12) без ограничения общности константа из (2) может быть положена равной единице.

Решая (10–12), находим множитель λ ₁:

max

0.5 J R( m ) R *( m ) { f  (0, m )exp( - i m t 0 ) Ф ( ю ) + f 2(0, m )exp( i m t 0 ) Ф *( m ) d m

л =

^m min

^m max

J R(m)R * (m)Ф(ю)Ф * (m)dm mmin

где введено обозначение:

ВЕСТНИК 2015

Φ ( ω ) = ₂ f ²(0, ω )exp( i ω t ₀) - f ²( θ ₀, ω ) exp( i ω t ₁) . (14)

ВЕСТНИК 2015

В итоге, спектр СШП импульса, обеспечивающий максимальное пиковое значение принимаемого сигнала, определяется выражением:

• 1    Г „ 2 * Г _ 2 *

V opt И = — R * И U (0, И - М (0, И - ^ 2 I -

• - V2 f² (9₀, ® )exp(- i® A t ) j, ⁽¹⁵⁾

где λ ₁ задаётся в виде (13, 14), ∆ t – разность времени прихода максимумов сигналов с направлений θ = 0 и θ = θ ₀, легко определяемая численно, например методом последовательных приближений. Нормирующий множитель λ ₂ находится при подстановке найденного спектра V_opt ( ω ) в (12).

На втором этапе решения задачи вначале определяем частоту ω ₀, на которой полуширина ДН f ( to 0 , 9 ) равна заданной 9 0 . Далее последовательно вводим значения ω _max > ω ₀ и ω _min < ω ₀, которые в итоге перекрывают либо весь частотный диапазон, используемый в радиолокации, либо достигают границ допустимой полосы частот, если она определена при постановке задачи. По формулам (13–15) для каждой пары значений ω _max и ω _min находится свой оптимальный спектральный состав СКИ и значение принимаемого сигнала U_M (0) из (1). Сравнивая полученные значения, находим максимум U_M (0), соответствующие ему граничные частоты ω_max и ω_min и оптимальный спектр генерируемого СКИ V_opt ( ω ) в виде (15).

Введя обозначение F[..] для преобразования Фурье, получим формы СШП импульсов: оптимального генерируемого

U_opt ( t ) = F[ V_opt ], (16) излучаемого в направлении θ – U_e ( t )= F [ V_opt f ( θ ) ], принимаемого с направления θ

U_r ( t ) = F[ V_opt f ² ( θ ) R ]. (17)

Пример 1 . Рассмотрим задачу обнаружения цели, защищённой сверхширокополосным радиопоглощающим покрытием. Радиолокационная цель описывается с помощью введённой функции R ( ω ) (6). Тип зависимости R ( ω ) выбран близким к частотной зависимости коэффициента отражения сверхширокополосного радиопоглощающего покрытия. Максимальные значения R ( ω ) приходятся на область низких частот, где электрическая толщина покрытия много меньше длины волны. На более высоких частотах значения R ( ω ) резко уменьшаются.

Были заданы максимально допустимая ширина ДН 2 θ ₀ = 3° и её форма на каждой из используемых частот, которая соответствовала форме ДН антенной решетки с равномерным распределением амплитуды тока по излучателям. Частота f и длительность импульса τ выражались в относительных единицах, так, чтобы выполнялось условие: fτ = 1, т.е. если частота f задаётся в ГГц, то τ – в наносекундах. Расчёты представлены в безразмерных величинах. За f ₀ = 1 выбрано значение частоты, на которой ширина

ДН равна 2 θ ₀, т.е. 3°. На этой частоте размер ан-

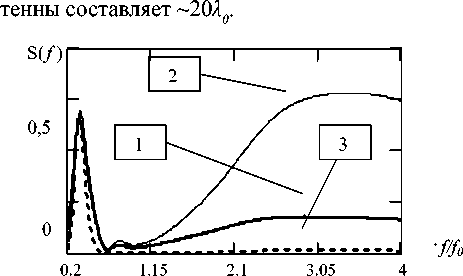
Рис. 1. Амплитудно-частотные спектры СШП импульсов 1 – генерируемый, 2 – излучаемый, 3 – принимаемый сигналы

На рис. 1 приведён найденный по формулам (13–15) амплитудный спектр генерируемого СШП импульса. Найденный импульс обеспечивает максимальное пиковое значение принимаемого сигнала при использовании очень широкой полосы частот: ∆ f = 0,2 f₀ ÷ 4 f ₀. На этом же рисунке показаны спектры излучаемого и принимаемого сигналов.

Форма принимаемых СШП импульсов в общем случае сильно отличается от генерируемых. На рис. 2 показаны найденный в соответствии с (16) генерируемый импульс и принимаемый импульс при угле наблюдения θ = 0°. Доля высокочастотных составляющих в спектре принимаемого импульса существенно ниже, чем в излучаемом, что приводит к сглаживанию сигнала и увеличению его длительности.

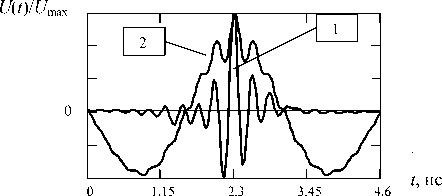
Рис. 2. Форма импульсов при угле наблюдения цели θ = 0°. 1 – излучаемый СШП импульс; 2 –принимаемый СШП импульс

Найденные значения максимумов U_M для различных частотных диапазонов приведены на рис. 3 в нормированном виде.

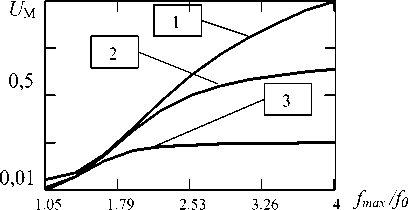
Рис. 3. Зависимость максимальных значений принимаемых СШП импульсов от высокочастотной границы спектра при различных значениях низкочастотной границы:

1 – f min = 0,2 f 0 ; 2 – f min = 0,35 f 0 ; 3 – f min = 0,43 f 0

Показаны изменения U_M при расширении спектра за счёт высокочастотной границы при различных фиксированных значениях низкочастотной границы f_min . При увеличении полосы для полученных зависимостей характерно резкое начальное возрастание максимальных значений и дальнейшая их стабилизация. Таким образом, хотя максимум U_M достигается при самой широкой полосе частот: 0,2 f₀ ≤ f ≤ 4 f₀ , сужение полосы до 0,3 f₀ ≤ f ≤ 3 f₀ снижает U_M лишь незначительно.

Обоснование эффективности применения СШП импульсов для обнаружения малозаметных целей

На основе решения приведенной задачи оказывается возможным провести количественную оценку улучшения характеристик обнаружения объектов и оценить потенциальные возможности использования СШП импульсов в радиолокации.

Главным критерием, в соответствии с которым следует проводить сравнение качества систем обнаружения и измерения координат радиолокационных целей при фиксированной ширине ДН, является отношение сигнал/шум в принимаемом сигнале – q . Обычно q ² определяют как отношение квадрата максимального значения полезного сигнала к среднеквадратичному значению шума [1]:

q ² = U M

^Un ²

.

Решение рассмотренной в предыдущем разделе задачи получения максимального значения принимаемого сигнала не обязательно обеспечивает максимальное значение отношения сигнал/ шум, т.к. увеличение полосы используемых частот приводит к возрастанию среднеквадратич- ного значения шума Un2. Для малозаметных целей при использовании узкополосных сигналов, когда полоса частот много меньше несущей частоты ∆ω << ω0, для угла наблюдения θ = 0° при условии единичной излучаемой мощности (12) из (5, 18) получим

2 = f (0, to ) 4 R ( to ) N 0 ( ^ 0 )

где N ₀ – спектральная плотность шума на частоте ω 0 .

При использовании СКИ отношение сигнал/ шум (18) в общем случае принимает вид:

,                 „                         ) ²

j V (to) f (0, to)2 R (to) exp( imt 0) dm k-W----------------------------L. (20)

w j N0 (to) dto

-w

Целесообразность использования СШП им- пульсов для решения задач обнаружения объ- ектов определяется степенью превышения qw2 значения q02, т.е. коэффициентом увеличения отношения сигнал/шум KW = qw2 /q02.

Значение KW для решенной задачи определения спектрального состава генерируемого СШП импульса из (19, 20) получаем в виде:

^KW ⁼

^ max

Re J V opt ( ® )f (0, ^ ) 2 R ( ^ )exp( i ® t o ) d ®

\ ® min                                             7 ;

×

^ 0 ⁽ ® 0 )

® max

J N₀( to) d m

® min

×

ВЕСТНИК 2015

f (0, ® o ) 4 | R ( ® o )|²

Функционал K_W оказывается зависящим от дисперсионных свойств ЭПР цели, а также от задаваемой максимально допустимой ширины ДН при приёме импульсов и дисперсионных зависимостей ДН антенной системы.

Решение задачи получения максимального K_W так же, как решение рассмотренной задачи получения максимального пикового значения принимаемого сигнала, разделяется на два этапа. Первый этап – поиск решения в виде V_opt ( ω ) для фиксированных значений ω_max и ω_min – у обеих задач совпадает. На втором этапе численно ищется максимум (21) по двум переменным ω _max и ω _min при уже полученной на первом этапе зависимости числителя (21) от этих переменных.

С вычислительной точки зрения поиск максимума функции двух переменных не представляет сложности.

Значения K_W для различных видов зависимости R ( ω ) могут различаться, поэтому для получения точных результатов требуется решать задачу поиска максимума (21) для каждой конкретной зависимости.

Пример 2 . Для получения численной оценки (21) используем те же исходные данные, что и в рассмотренном ранее примере 1. Шум будем считать «белым», его спектр N ₀( ω ) = N ₀. Тогда ²

K W

max

Re J Vopt(®)f(0,®)2R(®)exp(i®t0)d® v ®min f (0, ®o)4|R(®o)|2 (®max - ®min )

.

На рис. 4 приведена найденная в соответствии с (22) зависимость увеличения отношения сигнал/шум от низкочастотной границы спектра f_min при различных фиксированных значениях высокочастотной границы.

ВЕСТНИК 2015

K

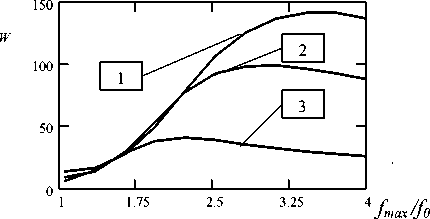
Рис. 4. Зависимость увеличения отношения сигнал/шум от высокочастотной границы спектра при различных значениях низкочастотной границы:

1 – f min = 0,2 f 0 ; 2 – f min = 0,25 f 0 ; 3 – f min = 0,275 f 0

Из полученных результатов следует, что отношение сигнал/шум для рассмотренных СШП импульсов много больше, чем при использовании узкополосных сигналов. Максимальное значение K_W составило 144 и было достигнуто при ширине полосы частот 0,2 f₀ ÷ 3,7 f₀ .

Применение оптимальной или квазиопти-мальной фильтрации позволяет ещё больше увеличить K_W . Максимальное значение K_W в этом случае составило 530 и было достигнуто при ширине полосы частот 0,2 f₀ ÷ 3 f₀ .

На практике, однако, значения функции R ( ω ), особенно её фазовой характеристики, могут быть заданы только приближённо. На математической модели исследовалась зависимость значений функционала K_W от точности задания коэффициента отражения цели R ( ω ). Среднеквадратичное отклонение δ ² характеристик отражения используемой модели цели от истинных значений определялось как

δ ²

ω max

∫ R ( ω ) - R M ( ω )² d ω

^ω min

ω max

∫ R ( ω ) ² d ω

ω min

,

где RM(ω) – используемая при математическом моделировании дисперсионная зависимость коэффициента отражения. Для корректного сравнения характеристик отражения была проведена нормировка ωmax

ω max

∫ R ( ω ) ² d ω = ∫ R_M ( ω )² d ω = 1 .

ω min

ω min

На рис. 5 приведена найденная статистическая зависимость коэффициента увеличения отношения сигнал/шум от среднеквадратической ошибки δ ². Показаны ошибки двух типов: в задании только фазочастотной характеристики отражения цели – (1) и в задании только амплитудночастотной характеристики – (2).

K W

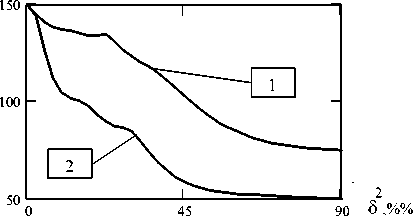
Рис. 5. Зависимость увеличения отношения сигнал/шум при приёме СШП импульсов от ошибки в задании: (1) – фазочастотной характеристики отражения цели;

(2) – амплитудно-частотной характеристики отражения цели

Полученные результаты моделирования свидетельствуют, что найденные решения являются устойчивыми. Среднестатистическое снижение значений коэффициента K_W даже при ошибках 50–90% составляет 2-3 раза по сравнению с максимально возможным.

Таким образом, оптимизация спектрального состава (или формы) СШП импульсов позволяет получать хорошие результаты даже при использовании приближённых данных о дисперсионной зависимости ЭПР цели.

Выводы. Применение СШП импульсов при радиолокационном обнаружении и измерении координат малозаметных целей позволяет резко повысить отношение сигнал/шум в принимаемом сигнале по сравнению с узкополосными РЛС. Достигнуто значительное, больше чем на два порядка, повышение отношения сигнал/шум во многом компенсирует снижение уровня отражения от целей, обусловленное применением сверхширокополосных радиопоглощающих покрытий [6].

В итоге можно констатировать, что полученные теоретические результаты и результаты численных экспериментов на математической модели показывают: применение СШП импульсов потенциально позволяет решать задачи радиолокационного обнаружения и измерения с необходимой точностью координат малозаметных целей, защищённых широкополосными поглощающими покрытиями, в том числе покрытиями типа «Стеллс».