Повышение маневренности быстроходной гусеничной машины с бесступенчатым механизмом поворота путем установки регулируемой гидродинамической муфты

Маневренность наряду с броневой защитой и вооруженностью является важнейшей тактикотехнической характеристикой быстроходной гусеничной машины (БГМ). Она включает в себя два ключевых условия, от степени соблюдения которых зависит ее качественная оценка – это устойчивость движения и управляемость. Устойчивость – способность возвращаться к прямолинейному движению или прежнему криволинейному при возвращении штурвала поворота в исходное положение – является необходимым, но недостаточным условием маневренности. Управляемость – способность БГМ реализовать кривизну траектории движения, заданную положением штурвала управления поворотом. Показателем маневренности служит средняя скорость движения. Поскольку она формируется при движении не только по прямолинейной, но и по криволинейной траектории, кривизна которой в реальных условиях движения постоянно меняется, средняя скорость во многом зависит от аспекта управляемости, а именно, от возможности используемого механизма поворота реализовывать на местности любую кривизну по желанию механика-водителя.

В мировой практике на быстроходных гусеничных машинах, для которых маневренность имеет определяющее значение, широкое применение нашли бесступенчатые механизмы поворота на базе гидрообъемных передач (ГОП) [8, 11]. Они позволяют обеспечить любой радиус и существенно снизить потери скорости на криволинейных участках, что в итоге позволяет увеличить среднюю скорость движения, и, как следствие, повысить маневренность БГМ. В настоящее время такие механизмы поворота устанавливают на всех основных танках и БГМ мира. Наиболее известные из них: американский танк «Абрамс M1A2», немецкие БМП «Мардер» и «Пума IFV» и танк «Леопард 2», израильский танк «Меркава МК4», в нашей стране – БМП-3. Однако несмотря на обеспечение неоспоримого качественного преимущества использование ГОП в механизме поворота несет в себе серьезный недостаток. Он заключается в потере управляемости БГМ при перегрузке ГОП по давлению, которая возникает в тяжелых условиях движения.

Для устранения этого недостатка существуют различные технические решения. Например, проблема перегрузки может быть снята установкой в механизм поворота более мощной и, как следствие, более дорогой ГОП, как было сделано в танке «Абрамс». Однако здесь мы сталкиваемся с такой проблемой, что сама возможность бесступенчатого регулирования кривизны, наряду с высокой удельной мощностью двигателя повышает вероятность потери устойчивости движения при неумелом управлении. Следует отметить, что потеря устойчивости движения является значительно опаснее кратковременной потери управляемости. Как альтернатива увеличению мощности в вопросе повышения управляемости существует другой подход, который заключается в установке вспомогательных устройств, направленных на снижение или предотвращение перегрузки ГОП. Преимущество и перспективность этого подхода заключается в больших возможностях по компоновке и организации совместной работы ГОП и вспомогательного устройства, что позволяет найти компромисс в решении задачи улучшения маневренности во всех аспектах. С одной стороны, в случае возникновения, – значительно снизить время перегрузки ГОП по давлению (время неуправляемого движения БГМ), другими словами, улучшить управляемость. С другой – организовать движение на пределе устойчивости, что исключит ее потерю при неумелом управлении. Таким образом, кроме улучшения показателя маневренности преимущество данного решения заключается в повышении безопасности механика-водителя во время движения.

Для перспективных образцов российских машин исследуется повышение управляемости путем установки в механизм поворота фрикционных муфт. Различные алгоритмы организации совместной работы ГОП и фрикционов показали свою эффективность [5, 6].

В немецких машинах в качестве вспомогательных устройств нашли применение регулируемые гидродинамические муфты.

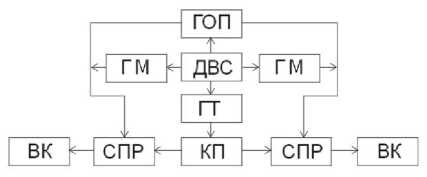
Для устранения проблемы потери управляемости на БМП-3 авторами было исследовано техническое решение, реализованное в немецких машинах «Леопард 2» и «Мардер», где параллельно ГОП работает регулируемая гидродинамическая муфта (ГМ), которая заполняется при перегрузке ГОП от ее предохранительного клапана и создает дополнительный поток мощности на вал гидромотора. Структурные схемы трансмиссий БМП-3 (базовой и усовершенствованной) с гидромуфтами для левого и правого поворота, представлены на рис. 1. Здесь ДВС – двигатель внутреннего сгорания; ГОП – гидрообъемная передача механизма поворота; ГТ – гидротрансформатор; СПР – суммирующие планетарные ряды; КП – коробка передач; ВК – ведущие колеса; ГМ – гидромуфта; стрелками обозначено направление потоков мощности.

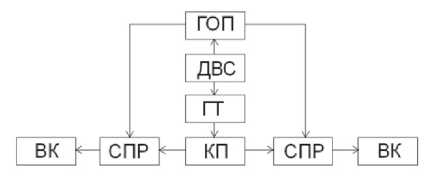
Рис. 1. Структурные схемы базовой и усовершенствованной трансмиссии БМП-3

В качестве метода исследования эффективности выбранного решения было использовано имитационное моделирование, при помощи которого воспроизводилось криволинейное движения БГМ с учетом нелинейностей характеристик грунта и гидрообъемной передачи, при этом – совместная работа ГОП и ГМ в условиях движения. Исследование выполнялось в среде VisSim с применением математической модели криволинейного движения БГМ, которая включает в себя описание как динамики движения корпуса машины, так и работы узлов и агрегатов внутри нее [2, 7, 12].

Работа двигателя смоделирована по внешней скоростной характеристике, что обеспечивает максимальную удельную мощность машины при различных режимах работы двигателя.

Моделирование движения БГМ проводилось в самых тяжелых для ГОП условиях, а именно: поворот с минимальным радиусом при условии резкого и полного поворота штурвала. Оценка эффективности работы устанавливаемой ГМ проводилась по двум параметрам: времени перегрузки ГОП и расходу предохранительного клапана.

Математическая модель, использованная в исследовании, создана на базе модели [7], разработанной на кафедре «КГМ» автотракторного факультета ЮУрГУ для исследования улучшения маневренности БГМ с независимым механизмом поворота и автоматической системой управления. Она дополнена в соответствии с темой и исходными данными исследования, что позволило применить ее для изучения влияния дополнительного потока мощности в механизме поворота на управляемость БГМ. Основу математической модели составляет система из 13 дифференциальных уравнений [7]. Первые 3 описывают перемещение корпуса машины в неподвижной декартовой системе координат. Остальные 10 - работу узлов и агрегатов внутри машины.

Поскольку модернизация состоит в установке регулируемой ГМ в оригинальный механизм поворота, используемый в БМП-3, в математическое описание работы механизма поворота включена ГМ. В соответствие с этим изменены дифференциальные уравнения, отвечающие за расчет угловых скоростей насосного колеса гидротрансформатора и вала мотора ГОП:

d^ = Г M ■ ч - М_н - М _н- i ₂ - M J ■ — , (1)

dT I Д 1 н гн 2 нк । j '

где ю н - угловая скорость насосного колеса гидротрансформатора, рад/с; Т - текущее время, с; М _д - момент двигателя, Н•м; М _н - момент насоса гидротрансформатора, Н•м; М_гн - момент насоса ГОП, Н•м; М _нк - момент на насосном колесе гидромуфты, Н•м; i 1 , i ₂ - передаточные числа в трансмиссии; J [ - момент инерции двигателя, кг•м².

d ® м dT

P - P )• R_BK ■ i₃

Mm - —--1 \    х3 + Мтк мтк

(к +1)J к + 1)

1 ■----------

J 3

где ю _м - угловая скорость мотора ГОП, рад/с; М м - момент мотора ГОП, Н•м; М _тк - момент турбинного колеса регулируемой ГМ, Н•м; P ₂ - сила тяги на забегающем борту, Н; P 1 - сила тяги на отстающем борту, Н; к - кинематическая характеристика бортового редуктора; к * - кинематическая характеристика суммирующего планетарного ряда; i ₃ - передаточное число в трансмиссии; J ₃ - момент инерции мотора ГОП, кг•м²; R _вк - радиус ведущего колеса, м.

Дифференциальное уравнение угловой скорости турбинного колеса гидротрансформатора заменено дифференциальным уравнением угловой скорости выходного вала коробки передач:

d^ ₌ М / ( ^P 2 + ^P 1 ^ ^ ^R вк ^ к * dT т к™ ( к + 1 ) . ( к * + 1 )

J 2 ,

где ю _£ - угловая скорость звена е на выходе из коробки передач, рад/с; М т - момент турбины гидротрансформатора, Н•м; i _кпп - передаточные число коробки передач; J ₂ - момент инерции, приведенный к звену е, кг•м².

Это позволяет в перспективе использовать в составе имитационной модели автоматическую коробку передач, просто заменив ею блок используемой механической.

В модели применен принцип суперпозиции для продольной и поперечной составляющих силы трения трака о грунт. Это удовлетворяет решению задачи и значительно упрощает работу. Силы тяги на бортах определяются в зависимости от буксования, что соответствует реальному процессу движения, кроме того, позволяет связать движение корпуса машины (внешние факторы) с работой узлов и агрегатов внутри нее (внутренние факторы). Для определения границы устойчивого движения в модели учитывается продольное смещение полюса поворота (х). Это необходимо и достаточно для достоверного описания устойчивого процесса криволинейного движения. Также в модели учтено перераспределение нормальных сил при повороте, что позволяет более достоверно описать процесс движения и обозначить границу устойчивости.

Расчетная схема движения гусеничной машины показана на рис. 2. Здесь X, Y - декартовы координаты положения корпуса машины на плоскости; ф - курсовой угол; МЦВ - мгновенный центр вращения; С, С 1 - центр тяжести и полюс поворота соответственно; P 1, P2 - силы сопротивления на отстающем и забегающем борту; VС - линейная скорость центра тяжести; VС бок - составляющая VС, направленная перпендикулярно оси корпуса машины; VС пр - составляющая VС, направленная вдоль оси корпуса машины; ω = dφ / dt – угловая скорость поворота корпуса; χ – продольное смещение полюса поворота; r – радиус траектории движения центра тяжести машины; R – расстояние от полюса поворота до МЦВ; L – продольная база машины; В – поперечная база машины; Pf1, Pf2 – силы сопротивления передвижению отстающего и забегающего борта соответственно; МСП – момент сопротивления повороту; Rб – боковая сила.

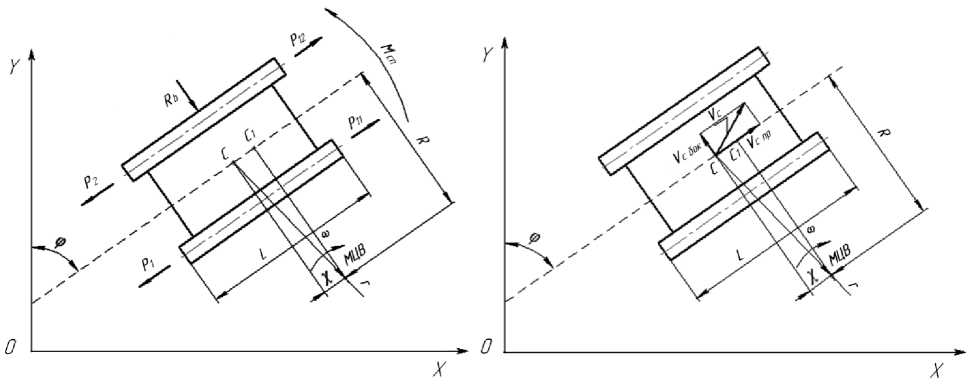
Рис. 2. Расчетная схема движения гусеничной машины, использованная в исследовании

Основные допущения, принятые в математической модели: не учтена упругость элементов двигателя, трансмиссии и ходовой части, не рассмотрены скоростные частичные характеристики дизельного двигателя, принято постоянство характеристик грунта; статические характеристики двигателя и гидротрансформатора; движение происходит в плоскости. Учет всех перечисленных параметров существенно усложняет математическую модель и перенацеливает ее на решение других задач.

С учетом принятых допущений в среде программирования VisSim [4] было проведено имитационное моделирование криволинейного движения базовой машины (без ГМ) для выбранных условий. При этом были получены следующие результаты: ГОП находилась в режиме перегрузки (а машина в режиме неуправляемого движения) в течение 1,587 с, максимальный расход жидкости через предохранительный клапан составил 23,5 л.

Для установки в трансмиссию из характеристик работы по угловой скорости и моменту на номинальном режиме работы двигателя согласно методике, описанной в [3], была выбрана гидродинамическая муфта с наиболее подходящей характеристикой коэффициента момента. Характеристика коэффициента момента является общей для серии геометрически подобных муфт. Это удобно тем, что позволяет легко рассчитать при помощи основного уравнения лопастных машин (4) момент любой конкретной ГМ, активный диаметр которой задан, а угловая скорость известна.

Основное уравнение лопастных машин имеет вид [1]

M= γ λD5ω2, (4) нк a нк где γ – вязкость рабочей жидкости (γ = 8600 Н/м3); λ – коэффициент момента ГМ; Da – активный диаметр ГМ (м); ωнк – угловая скорость насосного колеса ГМ (рад/с); Mнк – момент на насосном колесе ГМ (H·м).

Согласно алгоритму работы, устанавливаемая в механизм поворота ГМ заполняется от предохранительного клапана и тем самым включается в работу. Выводится из работы при помощи ее опорожнения путем соединения со сливной магистралью ГОП. Сложность расчета оптимальных параметров регулируемой ГМ заключалась в достоверном определении характеристики коэффициента момента в заданных условиях работы, а именно, степени заполнения и передаточного отношения ГМ. Первоначально было принято допущение о линейной зависимости коэффициента момента от степени заполнения. В основное уравнение лопастных машин был введен коэффициент заполнения ( K _Z ), равный отношению объема жидкости внутри ГМ к ее полному объему.

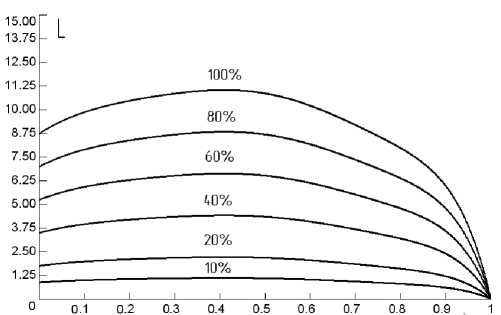
Рис. 3. Значения функции коэффициента момента λ от коэффициента заполнения K Z

При этом функция коэффициента момента изменялась (рис. 3). Здесь λ= L ⋅ 10 ^{- 4} ; i – передаточное отношение гидромуфты; в процентах показана степень заполнения гидромуфты.

Однако при имитационном моделировании с таким допущением были получены результаты, не согласующиеся с физикой процесса. Наиболее эффективной оказалась ГМ объемом 23,5 л и активным диаметром 0,4 м, передающая большой крутящий момент (170 Н·м) при очень низкой степени заполнения. Максимальное заполнение составляло всего 400 мл, что соответствует 1,7 % от всего объема. Полученные результаты показали на весьма приближенный характер расчета и наличие неучтенных факторов.

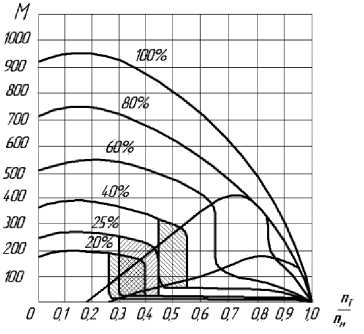
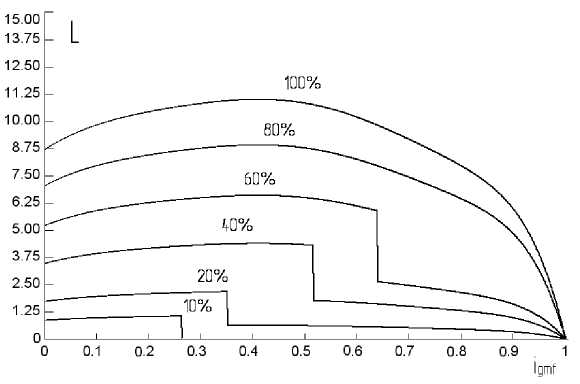
Из анализа литературных источников [1, 9, 10] было установлено, что коэффициент момента в зависимости от заполнения ГМ изменяется нелинейно и имеет скачкообразные переходы при достижении определенного соотношения параметров заполнения и передаточного отношения ГМ. Это связано с изменением схемы движения потока жидкости при переходе на другой устойчивый режим работы. На рис. 4 показаны диаграммы изменения коэффициента момента при различной степени заполнения ГМ. Слева – из литературного источника [10], полученная опытным путем для регулируемых ГМ, справа – аппроксимированная в соответствии с ней для выбранной ГМ с наиболее подходящей характеристикой коэффициента момента.

Следует акцентировать внимание на том, что задачей данной работы не являлся выбор самой лучшей из возможных регулируемых гидродинамических муфт для достижения цели улучшения маневренности, как и исключительно достоверное описание работы выбранной. Характеристика коэффициента момента, изображенная на рис. 4, б, при переменном заполнении выбранной ГМ может отличаться от соответствующей реальной характеристики. Главной задачей работы было выявление влияния переходных процессов, имеющих место при включении ГМ, на эффективность геометрически подобных ГМ одного типа, а также создание имитационной модели, позволяющей воспроизводить работу регулируемой ГМ в условиях переменного заполнения.

Здесь λ= L ⋅ 10 ^{- 4} ; i = n _т n _н – передаточное отношение гидромуфты; М – момент на турбинном колесе гидромуфты, в процентах показана степень заполнения гидромуфты.

а)

б)

Рис. 4. Диаграммы функции коэффициента момента λ от K Z с учетом нелинейности: а – из литературного источника; б – аппроксимированная для расчета в программе

Зависимости момента на турбинном колесе и коэффициента момента гидромуфты от ее передаточного отношения имеют одинаковую форму.

Получение более приближенной к реальному характеру изменения диаграммы (см. рис. 4, б) было достигнуто путем введения в расчет дополнительного коэффициента, названного коэффициентом переходного процесса ( K _пп ), который учитывает нелинейный харак т ер зависим о сти.

При этом основное уравнение лопастных машин приобрело вид

M_Kк = yX D_a ⁵ W 2_K K_z K_{v n}.                                                                 (5)

нк a нк Z пп

В ходе моделирования в среде программирования VisSim коэффициент заполнения ( K _Z ) и коэффициент переходного процесса ( K _пп ) были включены в блок-схему, отвечающую за расчет функции коэффициента момента. Блок-схема коэффициента момента (рис. 5) служит для определения в реальном времени его текущего значения в ра м ках всего диапазона изменения в зависимости от условий работы ГМ (ее передаточного отношения и степени заполнения) с учетом нелинейности. Состоит из нескольких частей.

Базовой частью является основная блок-схема, л евая часть которой служит для расчета функции коэффициента момента при полном (100 %) заполнении ГМ.

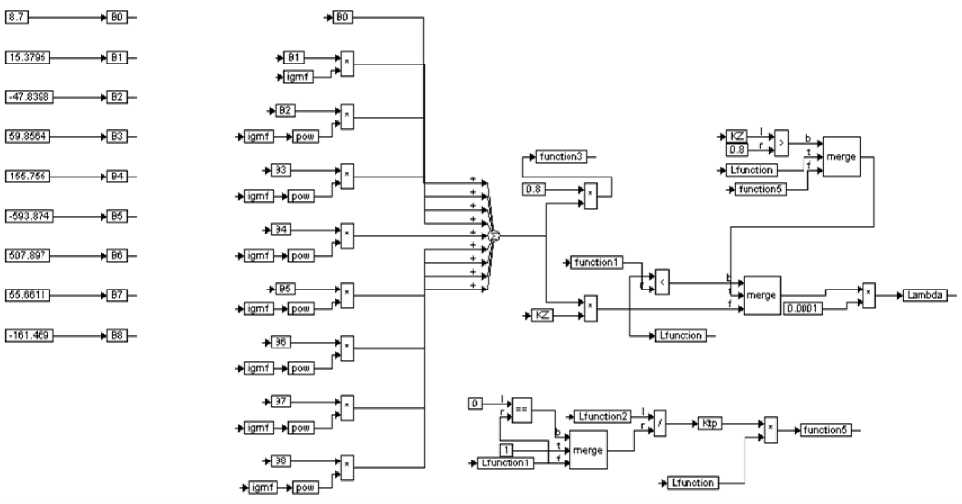
Рис. 5. Блок-схема по расчету функции коэффициента момента

Расчет функции коэффициента момента при полном заполнении ГМ осу щ ествляется при помощи ее аппроксимации в виде многочлена по формул е Тейлора. Для наибол е е точного о писания было взято девять ее характерных точек. Полученный многочлен имеет вид:

X = 8,7 + 15,3795i gm_f - 47,8398 i gmf + 59,8564 i gmf + 155,755 i gmf - 593,874 i gmf +

+507,897igmf + 55,6611igmf -161,469igmf, где λ – коэффициент момента гидромуфты; igmf – передаточное отношение гидромуфты.

В ходе моделирования многочлен умножается на текущее значение коэффициента заполнения, формируя функцию в соответствии с рис. 3.

На рис. 4, а показано, что при низкой степени заполнения переходный процесс происходит в некоторой зоне, обозначенной штриховкой. Для удобства определения ( K _пп ) было сделано допущение, что функция коэффициента момента совершает скачкообразный переход при д остижении некоторого определенного «критического» сочетания величин передаточ н ого отношения ГМ и степени заполнения, что характерно для ГМ с п о рогом. Для обозначе н ия всех сочетаний

«критических» величин, а также степени «скачка» в программе VisSim при помощи трех функций прямых была аппроксимирована область переходного процесса в соответствии с рис. 4, а.

На рис. 6 L = Х- 10⁴, А - верхняя граница переходного процесса, В - нижняя граница переходного процесса. Область ограничена функцией коэффициента момента при 80 % заполнении ГМ. При заполнении ГМ от 80 до 100 % коэффициент момента имеет линейную зависимость.

Переходный процесс осуществляется в случае пересечения сверху вниз функции границы «А» графиком Lfunktion, или его расположении ниже зоны переходного процесса. При этом текущее значение Lfunktion умножается на ( K _пп ), который рассчитывается как отношение функции «В» к функции «А» в момент пересечения. Допущение такого способа заключается в том, что после переходного процесса форма графика коэффициента момента остается неизменной, так как определяется

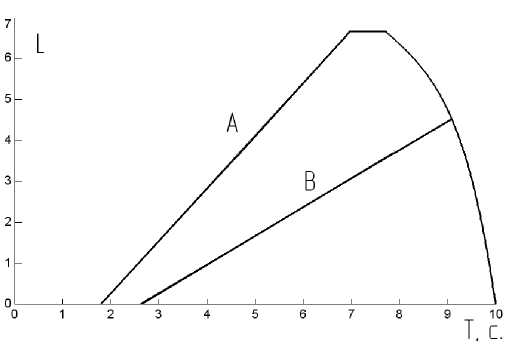
Рис. 6. Область переходного процесса

многочленом.

Как было коэффициента соответствии с

сказано ранее, график момента изменяется в изменением передаточ- ного отношения и заполнения ГМ. При этом значение (Kпп ) также непрерывно меняется. Важно акцентировать, что

Lfunktion и область переходного процесса формируются независимо друг от друга. Lfunktion – под действием передаточного отношения ГМ и ее заполнения, а область переходного процесса – под действием только передаточного отношения. Как следствие, возможна такая ситуация, когда при включении в работу ГМ Lfunktion сразу оказывается под зоной переходного процесса. Это делает невозможным в программе VisSim реализацию расчета (Kпп) из условия обязательного пересечения функций.

При решении использован неявный решатель Ньютона – Рафсона, который позволяет находить точку пересечения текущего графика Lfunktion с функцией границы «А» в реальном времени, даже если на самом деле пересечения не было, и тем самым непрерывно определять актуальное значение ( K _пп ). Определение точки пересечения происходит на каждом шаге симуляции путем подбора независимых переменных с точностью не менее 0,0001.

При пересечении или нахождении Lfunktion ниже функции «А» ее текущее значение умножается на ( K _пп), тем самым определяя значение функции коэффициента момента.

Коэффициент момента может совершать переходный процесс в обратном направлении. Для этого Lfunktion должна оказаться выше функции «В» (см. рис. 6).

Таким образом, введение дополнительного коэффициента позволило с более высокой точностью описать работу ГМ в условиях переменного заполнения и, как следствие, получить в ходе моделирования более точные геометрические параметры наиболее эффективной регулируемой гидромуфты.

При различных схемах расчета (без учета и с учетом переходного процесса) были получены сильно различающиеся результаты. При расчете с допущением о линейной зависимости, как было сказано ранее, наиболее эффективной оказалась ГМ с активным диаметром 0,4 м. При этом время работы ГОП в режиме перегрузки снизилось на 0,88 с (55 %). Объем жидкости, отведенный через предохранительный клапан ГОП, составил 400 мл. Муфта была заполнена на 1,7 %. При расчете с введенным коэффициентом переходного процесса ( K _пп ) наиболее эффективной оказалась ГМ с активным диаметром 0,15 м. При этом время работы ГОП в режиме перегрузки снизилось на 0,6386 с (40 %). Объем жидкости, отведенный через предохранительный клапан ГОП, составил 13 л. Муфта была заполнена на 100 %.

Для ГМ с активным диаметром 0,15 м диаграмма формирования коэффициента момента по времени в зависимости от заполнения и передаточного отношения представлена на рис. 7.

Начало работы ГМ происходит за зоной переходного процесса, чем объясняется скос диаграммы λ слева. При выведении из работы опорожнение ГМ осуществляется практически моментально, о чем свидетельствует скос диаграммы λ справа.

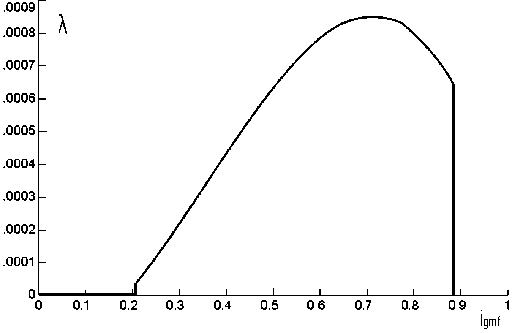
Рис. 7. Диаграмма формирования коэффициента момента

Таким образом, учет реальных особенностей работы заполняемой ГМ позволил правильно определить размер наиболее эффективной ГМ и тем самым обеспечить качественное регулирование работы бесступенчатого механизма поворота.

Выводы

В ходе работы была создана математическая модель регулируемой ГМ, позволяющая учитывать переходные процессы, возникающие при работе в условиях переменного заполнения. В связи с нелинейным характером изменения коэффициента момента ГМ в зависимости от степени ее заполнения, для более точного расчета при помощи основного уравнения лопастных машин, в уравнение введен дополнительный коэффициент, учитывающий нелинейность – «коэффициент переходного процесса». Расчет с использованием нового уравнения позволяет в большей мере учесть реальные особенности работы заполняемой ГМ и исключить получение неверных с физической точки зрения результатов.

Развита имитационная модель криволинейного движения БГМ для изучения проблематики улучшения маневренности БГМ в аспекте совместной работы ГОП и регулируемой ГМ. Проведено моделирование, которое показало работоспособность созданной математической модели, а также эффективность установки регулируемой ГМ параллельно ГОП. В ходе моделирования получены следующие результаты. На движение БГМ установка регулируемой ГМ, безусловно, оказала положительное влияние – время неуправляемого движения снизилось с 1,587 до 0,9484 с – на 40,2 %, как следствие, машина стала лучше входить в поворот. При повороте с минимальным радиусом 3,4 м использование ГМ дает преимущество в 0,3 м. Это составляет 10 % от величины реализуемого радиуса. Очевидно, что при повороте с большим радиусом в условиях перегрузки ГОП, например, при маневрировании при движении на скорости, численное значение этого преимущества будет возрастать. Таким образом, установка в гидрообъемный механизм поворота регулируемой ГМ, работающей по рассмотренному алгоритму, позволяет улучшить управляемость машины и, как следствие, повысить характеристику маневренности БГМ. По результатам моделирования сделан вывод о том, что наиболее эффективным является активный диаметр, при котором в условиях определенного алгоритма изменения коэффициента заполнения и передаточного отношения функция коэффициента момента не попадает в зону переходного процесса, но подходит ближе всего к его верхней границе.