Повышение работоспособности тракторов в сельском хозяйстве

Актуальность темы

Основные параметры обеспечения и повышения работоспособности машин в сельском хозяйстве разработаны 30-50 лет назад, и их нормативные значения в основном касаются образцов машин отечественного производства. Современные импортные тракторы и комбайны отличаются высококачественной сборкой, применением новых материалов деталей и технических жидкостей, выполняют комбинированные полевые работы на высоких скоростях. Заводы-производители разрабатывают свои методы и средства сервисного сопровождения, которые не учитывают специфику эксплуатации импортной техники на местах. Эти и другие свойства импортной сельскохозяйственной техники вызывают необходимость усовершенствования параметров технического сервиса с учетом местных эксплуатационных условий [3, 4].

Условия эксперимента и методика исследования

Причиной утраты работоспособности технических систем является целый комплекс факторов производства, эксплуатации, среды и других факторов, приводящих к старению или внезапному выходу из строя агрегатов и машин [4, 7].

Экспериментальные данные по факторам работоспособности импортных тракторов собирались в условиях реальной эксплуатации иностранной сельскохозяйственной техники в хозяйствах Иркутской области (ООО «Луговое», ЗАО «Иркутские семена», ООО «Барки», СХ ЗАО «Наследие», ООО «Колхоз Труд», в хозяйствах агрохолдинга СХОАО «Белореченское») методом периодических наблюдений. Объем выборки и длительность наблюдений оценивались доверительной вероятностью 0,8 и относительной ошибкой 10…15 %. Собранный материал обрабатывался и систематизировался согласно стандартным методикам [1, 2].

В результате наблюдений были выявлены группы общих и частных факторов потенциальной работоспособности импортных тракторов. Математическая модель зависимости показателя потенциальной работоспособности к от действующих факторов имеет вид:

F(k) = 0,03+0,45-к ртс +0,02-к ч +0,17 7-к с +0,22-к ти +0,18-к д ,

где к ртс - коэффициент, учитывающий влияние реального технического состояния; к ч - коэффициент, учитывающий влияние человека; к с - коэффициент, учитывающий влияние условий среды; к ти - коэффициент технического использования, учитывающий потери времени по организационным причинам; к д - коэффициент, учитывающий влияние недогруженности тракторов.

Для решения задачи и нахождения максимального значения показателя потенциальной работоспособности импортных тракторов, содержательный смысл которого заключается в максимальном состоянии готовности технического состава, использован известный в исследовательской практике разных производственных систем симплекс-метод, при использовании которого становится возможным решение линейных оптимизационных задач с приемлемой с математической точки зрения погрешностью [2, 5, 6].

Матрица коэффициентов при переменных модели работоспособности тракторов может быть представлена как:

1 x1 ... x j ... xn a00    a01   ...   a0j   ...   a0n k   a10    a11   ...

• ₁      10       11           a _{0 j    ...    a 1 n}

  
  

...

...        ...      ...     ...       ...    ...

• ‘   a i 0       a i 1     ...     a ij     ...     а 2 n

...

k m

• _ a m 0   a m 1    ...    a mj    ^... a mn

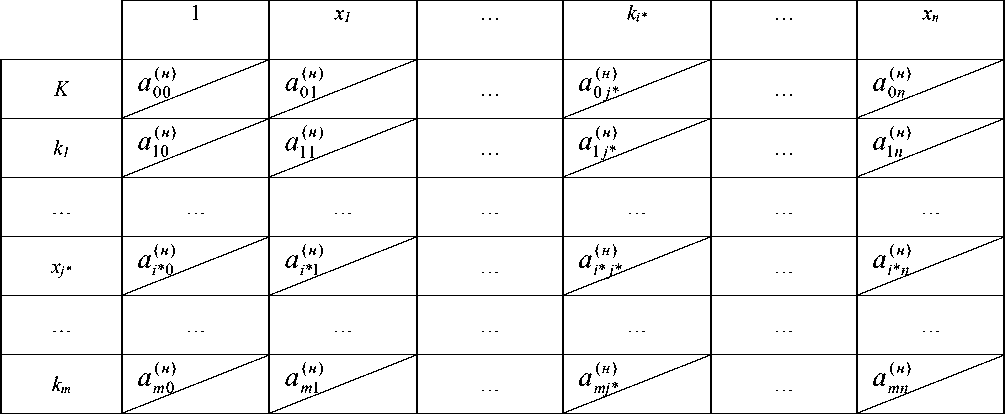
Первый шаг итерационной симплекс-процедуры начинается с таблицы 1, представленной коэффициентами матрицы (2), где переменные по строкам соответствуют базисным переменным, а по столбцам – свободным [2].

Преобразования очередной симплекс-таблицы

Таблица 1

	1		x 1			x j*			x n
K	a 00	a` 00	a 01	""a00		a 0j*	oa'oj*		a 0n	a On
k 1	a 10	""0'10	a 11	/aii		a 1j*	a'aij		a 1n	au in
k i*	a i*0	"0*0	a i*1	Otti‘1		a i*j*	0( 1 i*j*		a i*n	a i*n
k m	a m0	a mO	a m1	a ml		a mj*	a mi*		a mn	au mn

Среди отрицательных коэффициентов первой строки выделяют наибольший по абсолютной величине, а если таких окажется несколько, то любой из них. Пусть этот коэффициент соответствует свободной переменной x j* . Теперь необходимо x j* перевести в базис, заменив в нем некоторую переменную группы k i . Ту базисную переменную, которая быстрее обратится в нуль при увеличении x j* , следует сделать свободной. Это будет та базисная переменная k i* , для которой коэффициент в j -ном столбце ау* > 0 и отношение a io / ay- наименьшее. Столбец и строку, соответствующие свободной переменной x j* и базисной k i* , отметим в первой (очередной) симплекс-таблице двойными линейками (см. табл. 1) [2].

В таблице 1 в левом верхнем углу каждой клетки находятся коэффициенты a ij предыдущей симплекс-таблицы (в нашем случае - первой), а коэффициенты а'у , которыми заполнены нижние углы, соответствуют пересчету коэффициентов матрицы ограничений (1) в связи с тем, что базисная переменная k i* заменяется на свободную x j* . Коэффициенты а'у получаем по следующим правилам [2]:

• -    коэффициент на пересечении отмеченных строки и столбца a' *j* : a' * = 1 / a i*j* ;

• -    в клетках выделенной строки записываем верхние коэффициенты, умноженные на a' i*j* : a' * = a * • a' i*j* для j = 0,1, ..., j * - 1, j * + 1,..., n ;

• -    в клетках выделенного столбца записываем верхние коэффициенты, умноженные на a i*j* : a у* a y* * (— a i*j* ) для i 0,1,..., i * — l, i * + 1,..., m ;

• -    в клетках выделенной строки отмечаем особым способом верхние коэффициенты a ij* (кроме aij* ), а в клетках выделенного столбца - нижние коэффициенты a' i*j* (кроме a' i*j* );

• -    в остальных клетках записываем произведение выделенных особым способом коэффициентов, на пересечении которых стоит данная клетка: a' i*j* = a'i*j* • a4*j* * для i = 0,1,..., i - 1, i + 1,..., m и j = 0,1,..„j* - 1 ,j * + 1,..., п .

Затем переходим к заполнению таблицы 2, которая отличается от таблицы 1 тем, что отмеченная свободная переменная a'i*j* * стала базисной, а отмеченная базисная переменная a'i*j* * стала свободной [2].

Верхние левые клетки таблицы 2 (новые значения коэффициентов a 4*j* ) заполняются по следующим правилам [2]:

• 1.    Строка и столбец, соответствующие новым базисной ( i* -я строка) и свободной (j’ *-й столбец) переменным, заполняются нижними коэффициентами выделенных строки и столбца таблицы 1: a i*j = a'i*j* * для j = 0,1,..., п и a i*j = a'i*j* * для i = 0,1,..., m.

• 2.    В остальные клетки записываются суммы коэффициентов, состоящих в соответствующих клетках таблицы 1 a j ) = a'i*j* * + а' у для i = 0,1,..., i* - 1, i* + 1, .„m; j = 0,1,..., j* - 1, j* +1, … п .

Таблица коэффициентов

Таблица 2

Заполненная таким образом таблица 2 соответствует матрице коэффициентов (матрица 1) при новом составе базисных и свободных переменных. Отметим попутно, что a 'оо > 0, так как а 'оо является произведением положительных чисел а * (в силу допустимости предыдущего базисного решения) и а' оу* (в силу процедуры выбора j * столбца и правила формирования коэффициента а' оу* ). Следовательно, а 00) >  а оо и значение целевой функции работоспособности, соответствующее таблице 2, выше значения, полученного в таблице 1 [2].

Далее вся процедура повторяется до момента, когда на очередном шаге получается оптимальное (максимальное) решение [2].

Решение целевой функции (1) на максимум проводим при следующих условиях-ограничениях [1]

0,08 k ртс 0 + 0,19 k ртс 1 + 0,23 k ртс 2 + 0,14 k ртс 3 + 0,2 k ртс 4 + 0,2 k ртс 5 = 0,55,

0,12 k ч 0 + 0,17 k ч 1 + 0,17 k ч 2 + 0,15 k ч 3 + 0,2 k ч 4 + 0,21 k ч 5 = 0,63,

0,09 k c 0 + 0,19 k c 2 + 0,18 k c 3 + 0,17 k c 4 + 0,15 k c 5 + 0,24 k c 6 = 0,7,

0,11 k ти 0 + 0,21 k ти 1 + 0,22 k ти 2 + 0,17 k ти 3 + 0,17 k ти 4 + 0,14 k ти 5 = 0,64,

0,15 k д 0 + 0,21 k д 1 + 0,21 k д 2 + 0,24 k д 3 + 0,21 k д 4 = 0,81.

Решение состоит из двух этапов. Первый этап – введение искусственного базиса (единичной матрицы) и поиск первого опорного плана (без учета целевой функции). Второй этап – поиск оптимального решения на основе целевой функции [2].

Первый этап . Для нахождения начальной допустимой базы воспользуемся методом искусственного базиса.

Имеем:

Матрица коэффициентов A = a ij

0,08	0,19	0,23	0,14	0,2	0,2	1	0	0	0	0
0,12	0,17	0,17	0,15	0,2	0,21	0	1	0	0	0
0,09	0,19	0,18	0,17	0,15	0,24	0	0	1	0	0
0,11	0,21	0,22	0,17	0,17	0,14	0	0	0	1	0
0,15	0,21	0,21	0,24	0,21	0	0	0	0	0	1

Матрица b

В =

0,55 0,63 0,7

0,64 0,81

Проведя 7 итераций, определим, что вектор С не содержит отрицательных элементов. Первый этап симплекс-метода завершен.

Второй этап . Удаляем столбцы с искусственными переменными. Заменим вектор оценок С на целевую функцию.

Выразим базисные существенные переменные:

кртс = 0,0606-0,27к0-0,42 кч+0,12 кти, кд = 0,46+0,0682к0+0,5 кч+0,49 кти, кс = 3,32+0,86к0+1,25 кч+0,77 кти, которые подставим в целевую функцию:

F ( к ) = 0,03 к 0 + 0,45 к ч + 0,02 к ти + 0,18 (3,32+0,86 к 0 +1,25 к ч +0,77 к ти ) + 0,22 (0,0606-0,27 к 0 -0,42 к ч +0,12 к ти ) + 0,18(0,46+0,0682 к 0 +0,5 к ч +0,49 к ти ) или

F ( к ) = 0,68 - 0,0751 к ртс + 0,23 к д - 0,23 к с .

Имеем:

Матрица коэффициентов A	= a y
	0,08	0,19	0,23	0,14	0,2	0,2
	0,12	0,17	0,17	0,15	0,2	0,21
А =	0,09	0,19	0,19	0,17	0,15	0,24
	0,11	0,21	0,22	0,17	0,17	0,14
	0,15	0,21	0,21	0,24	0,21	0

Матрица b

В =

0,55 0,63 0,7

0,64 0,81

Проведем две итерации и определим, что значение целевой функции: F ( к ) = b x c = 0,9.

Выводы

Повышение работоспособности техники как отечественного производства, так и зарубежного является востребованной производственной задачей. Однако зачастую импортные машины превосходят, а в некоторых случаях и вовсе не имеют аналогов среди образцов отечественной продукции. Более высокий срок службы и уровень надежности сочетаются с комфортом, а также с тем, что при соблюдении сроков планово-предупредительных мероприятий машины зарубежных брендов могут служить до 30 лет и более.

Методика решения экстремальной экспериментальной задачи установлением максимального значения показателя работоспособности импортных тракторов позволяет выделить факторы, интенсивность использования которых с приемлемой погрешностью достигается путем вариации коэффициентов реального технического состояния, технического использования и потерь производительности тракторов.