Повышение разрешающей способности с помощью вытянутых сфероидальных волновых функций

Проблема повышения разрешающей способности при восстановлении изображений имеет актуальное значение. Набор ортогональных функций, которые оказываются очень полезными в проблемах экстраполяции и интерполяции на некотором интервале, называются вытянутыми сфероидальными волновыми функциями (ВСВФ). Их использование в этих задачах было первоначально представлено в работах [13], а затем и в других работах [4-10].

При получении изображения оптическими системами с ограниченным зрачком происходит его искажение и потеря информации, связанная с усечением спектра. Для восстановления сигнала может быть применен метод аналитического продолжения спектра [10]. При этом используется разложение известной части спектра в различные функциональные ряды, например в ряд Котельникова [11]. Наиболее удобным оказывается разложение по системе ВСВФ, так как они обладают свойством двойной ортогональности: образуют ортогональную и полную систему как на ограниченном, так и на неограниченном диапазоне.

В данной работе проведено сравнение данного подхода повышения разрешающей способности одномерных сигналов с линейной интерполяцией и интерполяцией с помощью функций отсчетов (ряд Котельникова). Заметим, что одномерный случай легко обобщается на двумерный для прямоугольного зрачка.

где *

- знак свертки, n ( t ) =

[ 1, t e [ - 0,5, 0,5 ] [ 0, t « [ - 0,5, 0,5 ].

При этом v _n ( t ) и X _n являются непрерывными функциями параметра

c = 2 w_cT .

Из (2) видно, что энергия в W _n ( t ) подвергается сначала усечению, а потом фильтрации. Таким образом, каждый A n будет иметь значение меньше единицы. Обычно их выбирают так, чтобы они были положительными и упорядоченными по убыванию:

1 >Х о >X 1 > ... >  0. (4)

Из (2) также следует, что ВСВФ являются точно полосо-ограниченными и, таким образом, не искажаются низкочастотной фильтрацией:

V n ⁽ t ) = V n ⁽ t ) * ² w c ^sinc(2 w c t X

³ [ V n ⁽ t ^{) ]} = ³ [ V n ⁽ t ) ] • n| - w - I, I ² w c J

1. Вытянутые сфероидальные волновые функции нулевого порядка

ВСВФ нулевого порядка могут быть определены как решение интегрального уравнения:

T /2

A n V n ( t ) = 2 W c J V n ( t )sinc[2 W c ( t - T )] dT,

- T /2

t _e [-»,да],

где 0 <  n < да и A n - собственные значения,

sinc( t )=sin( t )/ t ;

ВСВФ могут таким образом быть рассмотрены как собственные функции низкочастотной фильтрации ограниченных сигналов:

^X n V n ⁽ t ) =

V n ( t )П^ T ^

* 2 w_c sinc(2 w c t ),

где 3 - знак преобразования Фурье.

На бесконечном интервале для заданного параметра с ВСВФ являются ортонормированными:

J V n ( T ) V m ( T ) d T = £ [ n - m ]                  (6)

-да и образуют полный базисный набор для полосоограниченных сигналов с ограниченной энергией. То есть, если f(t) - полосо-ограниченная, то f (t) = Е anVn (t), n=0

a n = J f ( t)w_n ( t ) dt .                           (7)

-да

На конечном интервале 1 1 | < T ^z2 для заданного параметра с ВСВФ ортогональны:

T /2

J V n ^{( T} ) W m ^{( T} ) d ^T = ^A n ^{5 [}n ^{- m ]              (8)}

- T /2

и образуют полный базисный набор для функций на интервале | 1 | < T /2 с ограниченной энергией:

NT

h(t) = Е bn V n(tX И<у, n=-N             2

T /2

^A n b n = J h ⁽ t) W n ⁽ t ) ^dt .                      ⁽⁹⁾

- T /2

ВСВФ являются также собственными функ

циями вида преобразования Фурье:

V n ( t ) ^

T | Tw || w I

V _n l I n| I .

2 w c X _n   | 2 w c J | 2 w c J

ниям спектра на конечном интервале. Вследствие полноты системы ВСВФ в множестве функций с финитным спектром, ряд сходится к F ( w ) [10].

Восстановленный сигнал f ( t ) вычисляется как обратное преобразование Фурье от F ( w ). Тогда

Аналогично для усеченных ВСВФ:

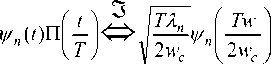
2. Применение ВСВФ для аналитического продолжения спектра

да

f ⁽ t ) = X a n ³—^ n ^{( w ) ]} .                  ⁽¹⁶⁾

n = 0

Используя свойство инвариантности ВСВФ к преобразованию Фурье на ограниченном интервале, восстановленный сигнал находится по формуле [10]: f ( t ) =

Пусть оптический прибор, формирующий изображение g ( t ) исходного сигнала ftt ), состоит из телескопической системы линз L 1 , L 2 и диафрагмы D

= S

⁰ I t l

T

> —

4 nw₀ ”

—X a n

T     n = 0

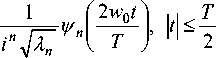
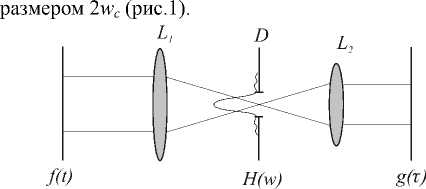
Рис. 1. Телескопическая система с ограниченным зрачком.

Без учета шумов искажение в такой изображающей системе вносится за счет дифракции Фраунгофера на диафрагме и может быть описано следующими соотношениями:

g ^{( т )} = 3 ¹

N ( t > ] -^п|^^|) .

c

g ( т ) = f ( t ) * 2 w c sinc (2 w_ct ).

Учитывая, что ВСВФ инвариантны к преобразованию (12) (см. ур. (5)), предлагается именно их использовать для восстановления сигнала f ( t ) по изображению g ( t ).

Рассмотрим алгоритм восстановления с аналитическим продолжением спектра.

Пусть F 0 ( w ) будет полосо-ограниченной функцией с известной шириной 2 w₀ . Задача экстраполяции состоит в восстановлении F ( w ) из

( I

Fo(w) = F(w)n|-w- |.(13)

1 ^{2 w} 0 J

Разложим F ( w ) в ряд по ВСВФ:

да

F(w) =Е an V n (w)

n = 0

где

1 ^w 0

an =Г" Fw)Vn(w)dw.(15)

X n - w 0

В силу двойной ортогональности ВСВФ, разложение (14) существует для всех значений w е [- да , да ], хотя коэффициенты a n вычисляются по значе-

Рассмотрим следующий пример. Волновое представление телефонного разговора может быть рассмотрено как полосо-ограниченное. Следуя по лученным результатам, можно сделать вывод, что этот разговор можно восстановить, если известно только слово или два в середине. Это, конечно, неверно. Дело в том, что на практике известна часть сигнала, сопровождаемая некоторым шумом. Для определения влияния шума на алгоритм, мы должны исследовать структуру собственных значений.

2 c -

Известно [1], что для n <— собственные зна-п чения Xn существенны, затем с ростом n происходит быстрый их спад до нуля. Рассмотрим теперь оценку коэффициентов в (15), когда значения F0(w) сопровождаются малой степенью неточности. Если n 2c выше порога — , то деление на X n ® 0 будет силь-п но увеличивать ошибку. Таким образом, коэффици енты an могут быть вычислены достоверно до это- го порога.

• 3.    Численные результаты по восстановлению сигнала

Рассмотрим задачу, состоящую в том, чтобы по имеющимся отсчетам сигнала восстановить значения в точках, лежащих между данными отсчетами. Данную задачу также можно решить методом аналитического продолжения спектра.

Будем использовать априорную информацию о конечной протяженности изображения , то есть все отсчеты f ( t ) расположены на конечном интервале [- T /2, T /2], вне пределов этого интервала она равна нулю.

Спектр исходного сигнала ft ) c учетом наложенных на нее ограничений, считается по формуле:

T /2

F ( w ) = J f ( t )exp( - 2 n itw ) dt              (18)

- T /2

Для дискретных сигнала и спектра (18) примет вид:

N /2

F ( mh w ) = 2 f ( nh )exp( - 2 n inhmh w )    (19)

n =- N /2

где h -шаг дискретизации ftt ), h w - шаг дискретизации F ( w ) , N - число отсчетов спектра и сигнала.

С другой стороны дискретный спектр:

F ( m ) =

( f (n) expl - 2niI

I

N /2

- N /2

Из сравнения (19) и (20) получаем hhw = N ^ hw = 1(21)

Таким образом, с помощью (20) получается дискретный спектр до частоты не выше wc =1 Nhw = —.(22)

c 2 w 2 h

Уравнение (22) задает связь между полосой пропускания w c и шагом дискретизации наблюдаемой функции. То есть чем шире полоса пропускания, тем точнее будет известна наблюдаемая функция. Но на практике трудно реализовать прибор с широкой полосой пропускания. Для повышения разрешения функции можно экстраполировать спектр за пределы интервала [- w c , w c ].

Задачу сверхразрешения можно также решить путем интерполяции сигнала внутри интервала [- T /2, T /2]. Далее будут рассмотрены алгоритмы и представлены результаты интерполяции сигнала и экстраполяции спектра, а также проведено сравнение этих методов.

Для численных экспериментов по восстановлению исходный сигнал f ( n ) прореживаем в несколько раз, прореженный сигнал обозначим g ( n ). Далее восстанавливаем прореженный сигнал до размерности исходного, получаем f ( n ). На рис. 2

приведены примеры восстанавливаемых сигналов прямоугольной и синусоидальной формы с высокочастотными всплесками.

Среднеквадратичное отклонение считается по формуле

8 ²

N A²              2

2   f ^{( n} ) ^- fⁿ )

n =- N /2 ____________

N /2     ,

2 I f ( n )|²

n =- N /2

• 4.    Метод линейной интерполяции

Это самый простой метод интерполяции сигнала. Мы имеем значения исходного сигнала в некоторых точках. Значения функции в точке, расположенной между известными отсчетами, рассчитываются по формуле: f ( t ) =

= §[( n- 1) h ] . ^: g ⁽- ^{nh )} g l’- n ^{l) h} l l -^[ ' ⁽- n ^{l) h} l . ⁽²⁴⁾ h

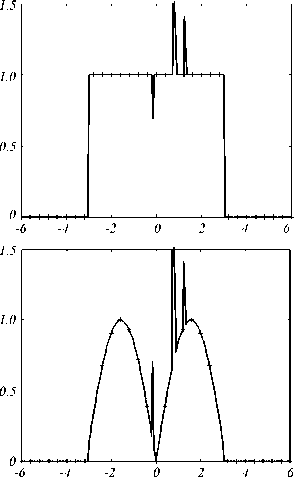
Рис.2. Исходный (сплошная линия) и прореженный сигналы (отмечены "+").

На рис. 3 представлены исходный сигнал и сигнал, восстановленный из прореженного в 8 раз с помощью линейной интерполяции. Погрешность восстановления для прямоугольника - 8 2 =0,1919, для

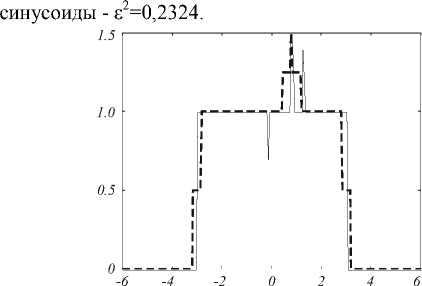
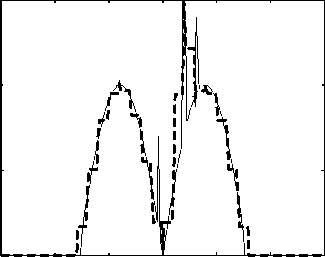
Рис. 3. Линейная интерполяция: исходный сигнал (сплошная линия) и восстановленный из прореженного в 8 раз (пунктирная линия).

• 5.    Метод функций отсчетов

Рассмотрим теперь интерполяцию сигнала при помощи разложения исходной функции в ряд по функциям отсчетов. Согласно теореме Котельникова любую непрерывную функцию можно представить в виде:

f ( t ) = ⁺∑^∞ f ( nh ) sⁱn² π ^{wc ( t - nh )} ,         (25)

_{n =-∞}         2 π w_c ( t - nh )

где f(nh) - дискретная с шагом h функция.

В нашем случае можно восстановить значения функции между отсчетами по формуле:

^{N /2}         sin 2 π w ( t - nh )

f ^€( t ) = ∑ g ( nh )        ^c                (26)

_{n =- N /2}         2 π w_c ( t - nh )

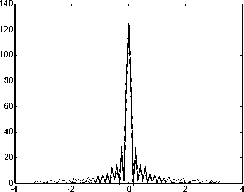
На рис. 4 представлены результаты восстановления сигнала из прореженного в 8 раз с помощью функций отсчетов (26). Погрешность восстановления для прямоугольника - ε2=0,1681, для синусоиды - ε2=0,2392.

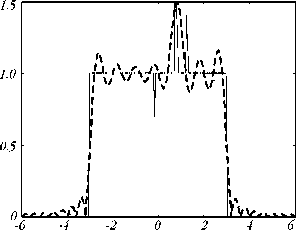
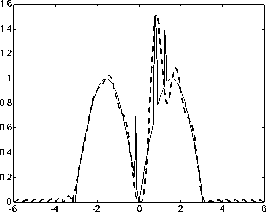
Рис. 4. Восстановление с помощью ряда Котельникова: исходный сигнал (черный цвет) и восстановленный из прореженного в 8 раз (синий цвет).

• 6.    Метод ВСВФ

Этот метод подробно описан в разделе 2. Для экстраполяции спектра была использована формула M

F ( w ) = ∑ a_n ϕ _n ( w ) , n = 0

2c где M= π -2, w=nthw, nt=-Nk/2:Nk/2, N - число отсчетов прореженного сигнала, k - во сколько раз хотим продлить спектр, hw- шаг спектра.

Коэффициенты a n считаются по формуле (15) методом прямоугольников.

На рис. 5 изображена наиболее информативная часть спектра исходного сигнала и экстраполированного методом ВСВФ из усеченного в 8 раз. Погрешность аппроксимации для спектра прямоугольника - ε²=0,103, для синусоиды - ε²=0,029. Приведенные результаты получены для с =20. Учитывая, что сигнал имеет протяженность [-3,3] (рис. 2, 3), то есть T =6, то из формулы (3) w c =1,67. Если повысить с , а следовательно число используемых функций, то можно получить лучшие результаты.

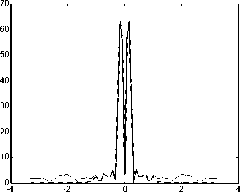
Рис. 5. Экстраполяция усеченного в 8 раз спектра методом ВСВФ: спектр исходного сигнала (черный цвет) и экстраполированный спектр (синий цвет).

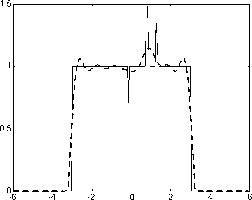
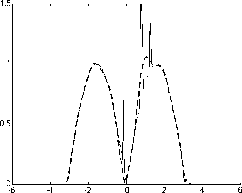
Рис. 6. Восстановление с помощью экстраполяции спектра по ВСВФ: исходный сигнал (черный цвет) и восстановленный из усеченного в 8 раз спектра (синий цвет).

На рис. 6 представлены результаты восстановления сигнала из усеченного в 8 раз спектра с помощью ВСВФ. Погрешность восстановления сигнала для прямоугольника - ε2=0,1274, для синусоиды -ε2=0,1613.

В таблице 1 приведены погрешности восстановления перечисленными методами для разной степени прореженности k прямоугольного сигнала, а в таблице 2 - для синусоидального сигнала.

На рис. 7 показаны графики погрешности восстановления перечисленными методами в зависимости от степени прореженности k для прямоугольного (рис. 7а) и синусоидального сигналов (рис. 7б). Из графиков на рис. 7 видно, что выигрыш метода ВСВФ достигается при усечении спектра в 4-6 раз.

Таблица 1. Погрешности восстановления сигнала в зависимости от степени прореженности к для прямоугольного импульса

Степень прореженности, k	Метод линейной интерполяции	Метод функций отсчетов	Метод ВСВФ	Аппроксимация спектра с помощью ВСВФ
2	0,0777	0,0839	0,1198	0,0951
4	0,1297	0,1459	0,1211	0,0956
6	0,1644	0,1902	0,1237	0,0981
8	0,1919	0,1681	0,1274	0,1030
10	0,2074	0,2457	0,1416	0,1208

Таблица 2. Погрешности восстановления сигнала в зависимости от степени прореженности к для синусоидального сигнала

Степень прореженности, k	Метод линейной интерполяции	Метод функций отсчетов	Метод ВСВФ	Аппроксимация спектра с помощью ВСВФ
2	0,1238	0,0918	0,1613	0,0296
4	0,1624	0,1409	0,1614	0,0296
6	0,2079	0,1771	0,1613	0,0296
8	0,2324	0,2392	0,1613	0,0294
10	0,2387	0,1788	0,1620	0,0166

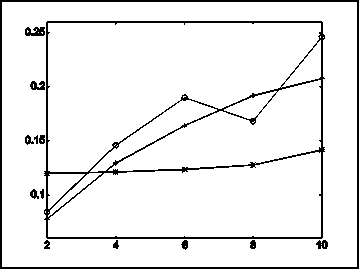
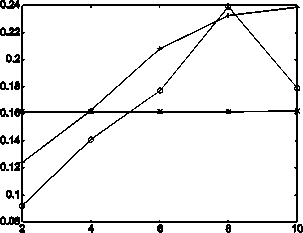
Рис. 7. Графики погрешности восстановления сигнала в зависимости от степени прореженности к линейной интерполяцией (линия с "+"), рядом Котельникова (линия с "о") и метод ВСФВ (линия с "*") для прямоугольного (а) и синусоидального сигналов (б).

Заключение

В данной работе проведено сравнение метода повышения разрешающей способности одномерных сигналов, основанного на использовании вытянутых сфероидальных волновых функций нулевого порядка, с линейной интерполяцией и интерполяцией с помощью функций отсчетов (ряд Котельникова).

Показано, что выигрыш метода ВСВФ восстановления сигнала при прохождении изображающей системы с ограниченным зрачком наступает при усечении спектра в 4-6 раз.

Работа поддержана Российским фондом фундаментальных исследований (гранты 00-15-96114, 00-01-00031).