Повышение стабильности функционирования рабочего органа в кривошипных прессах
Автор: Кобзев К.О.
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Машиностроение и машиноведение
Статья в выпуске: 4 т.19, 2019 года.
Бесплатный доступ
Введение. Исследованы статическая и динамическая системы нагружения предохранительной фрикционной муфты (ПФМ). Синтезирована принципиальная схема фрикционного контакта твердых тел в кузнечно-штамповочных машинах. С точки зрения исследования процесса повышения стабильного функционирования рабочего органа в кривошипных прессах рассмотрены следующие факторы: время срабатывания, текущий коэффициент трения и изменение вращающего момента при статическом и динамическом нагружении предохранительной муфты. Материалы и методы. Определено время срабатывания ПФМ, имеющей дифференцированные пары трения. Искомый показатель соответствует участку рабочего времени, на котором усиливается нагружение (между значениями номинального вращающего момента и момента срабатывания). Параметры системы, состоящей из двух масс, соответствуют параметрам эквивалентной системы, включающей муфту и ключевые части привода. Элементы системы: масса инерции; масса инерции, включающая ротор двигателя и основную (ведущую) часть ПФМ; упругая связь с указанным значением приведенной угловой жесткости...
Кривошипный пресс, коэффициент трения, рабочий механизм, коэффициент усиление, перегрузка, точность
Короткий адрес: https://sciup.org/142221972
IDR: 142221972 | УДК: 621.825.54 | DOI: 10.23947/1992-5980-2019-19-4-374-381
Текст научной статьи Повышение стабильности функционирования рабочего органа в кривошипных прессах
1Don State Technical University, Rostov-on-Don, Russian Federation
Введение. На современном этапе развития производства актуально повышение надежности и увеличение срока эксплуатации производственного оборудования. В частности, представляет интерес исследование статической и динамической систем нагружения предохранительной фрикционной муфты. В рамках данной работы исследована статическая и динамическая системы нагружения предохранительной фрикционной муфты. Синтезирована принципиальная схема фрикционного контакта твердых тел в кузнечно-штамповочных машинах. С точки зрения исследования процесса повышения стабильной работы рабочего органа в кривошипных прессах рассмотрены следующие факторы: время срабатывания, текущий коэффициент трения и изменение вращающего момента при статическом и динамическом нагружении предохранительной муфты.
Материалы и методы. Определим время срабатывания предохранительной фрикционной муфты (ПФМ), имеющей дифференцированные пары трения. Искомый показатель соответствует участку рабочего времени, на котором усиливается нагружение, — между значениями T н (номинальный вращающий момент) и T i (момент срабатывания). Параметры системы, состоящей из двух масс, соответствуют параметрам эквивалентной системы, включающей муфту и ключевые части привода (рис. 1).
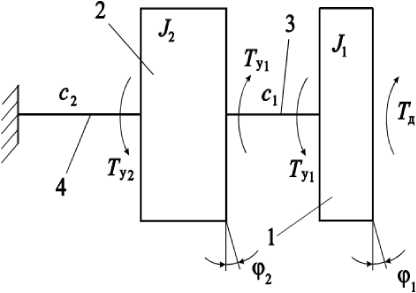
Рис. 1. Расчетная динамическая схема 1
Составные части системы:
— масса инерции (эквивалентная система подведена к основному (ведущему) валу ПФМ (позиция 1 на рис. 1.); — масса инерции, включающая ротор двигателя и основную (ведущую) часть ПФМ (позиция 2 на рис. 1);
— упругая связь с указанным значением приведенной угловой жесткости с 1 и с 2 соответственно (позиции 3 и 4 на рис. 1).
Установим, что значение демпфирования в этой системе и в ПФМ низкое, и его не следует использовать. Значение приведенного момента сил сопротивления равно T н . Учитывая эти факторы, получаем уравнения движения [1]:
^1 + С 1 ( ф 1 -ф 2 ) = Т д , (1)
J 2 ф 2 + с 2 ф 2 = с 1( ф 1 -ф 2 ), (2)
Машиностроение и машиноведение
где J1 , J2 — значения приведенных моментов инерции соответственно ПФМ и неосновной (ведомой) части привода; -д — значение движущего момента; ф1, Ф2 — значения обобщенных координат движения системы (значения углов поворота масс инерции соответственно 1 и 2).
Уравнения (1) и (2) показывают, что двигатель обладает необходимым ресурсом значения мощности и ф 1 = ю 1 ( го — значение угловой скорости движения масс инерции 1, to = const, 1 — значение времени) [2-5].
Введем данные условия в уравнение (2):
c + c c ф 2 + ф 2 = J Ю 1 .
J 2 J 2
В итоге запишем:
ф 2 = A sin
' c + c c + c o c
—---2 1 + B cos 1---2 1 +--1— to 1 .
J 2 у J 2 c 1 + c 2
Значения постоянных интегрирования A и B необходимо вычислять при указании начальных значений: при 1 =0 ф 2 = Т н / c 2 , ф 2 = ю . Тогда
Т
B = -н; A = c2
c 2 Ю J 2
q + c 2 c l С1 + c 2
Отсюда
, co Ю Jo . /c + co - c + co c ф2 = —2— --— sin —--21 + — cos 1--21 +--1— Ю1 .
c1 + c 2 Mc1 + c2 MJ2 c 2 у J2 c1
Значения нагрузок, которые получают упругие связи 3 и 4, равны:
cc Ю 1 c i c o Ю J o . c + c o c c + c o
-
-1 = q (ф1 - ф2) = ---12 --2— sin P---21 —1 -h cos P
-
c1 + c2 c1 + c2 cM + c 2 V J2 c2
-
c i c oЮ 1 c оЮ J o . /c + c c + c o
To = co фо = --1--2 ---2— sin 1---21 + -„ cos 1
2 22
q + c2 q + c2 у c + c2 у J2у c + c c + c c + cc sin 1---21 = 0 , cos 1---21 = 1 или sin p---21 = 1, cos p---21 = 0 .
J2 J2 J2
Рассмотрим уравнение:
-
с 1 с 2 Ю I J 2 _ c 1 -с 1 + с 2 V c 1 + c 2 c 2 н
Единственное действительное значение решения уравнения (6): г^
-
1 C^J о Ю
-
C1 = с2 3----2
-
- 2H
V v н
Анализ кубического уравнения
3 2 2 3 с 2J 2Ю с 1 + 3C 1C2 + 3C1C 2 + с 2--2
Tн
позволяет сделать следующее утверждение: при значениях переменных с 1 , меньших, чем значение переменной, вычисленной по (6), значение левой части (7) намного больше правой [6–8]. При указанных в (3) тригонометрических функциях с возможным уменьшением с 1 увеличивается значение амплитуды колебаний по синусоиде ( С 1 С 2 Ю ^J 2 / ( C 1 + C 2 ) /( C 1 + C 2 ) ) и уменьшается значение амплитуды колебаний по косинусоиде ( c 1 - h / c 2 ) .
с 1 < с 2
3 с 2 J 2 Ю
н
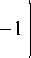
Отрезок времени, когда значение момента упругой связи 3 является идентичным T п :
t c
c i + c 2 c 1 c 2 to
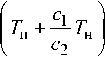
Тогда sin^( c i + c 2 ) t c / J 2 = 0 ; cos^( c i + c 2 ) t c / J 2 = 1, вследствие чего находим:
V ( c l + c 2 ) t c / J 2 = 2 n n ,
где n = 0, 1, 2,…., n .
Учитывая (9), запишем:
( C l + с 2)^ C l + с 2 I Тп + — Т н I = 2 n nJ 2 C 1 C 2 to .
Для жестких ПФМ | q > c 2 1 3 c 2 J 2 to 2/ T 2 H - 1 || используем выражение cos ( c i + c 2 ) t c / J 2 = 0. При этом
_ c i + c 2 C , c i c 2 to I J2\ ' t c T H + .
c^ to ^ c i + c 2 ^ q + c 2 J
В данном уравнении угловая жесткость ПФМ:
sinV( c i + c 2 ) t c / J 2 = i,
C i + C o П _
^--- 2 tc = — + 2 n n .
J 2 c 2
Значение можно получить в форме аналитического итога:
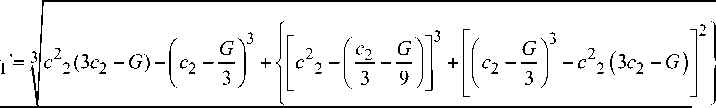
> +
+ 3 3
c 22 (3 c 2 — G ) —
G c 2 — 7
— ^ c 22
—
c 2
G
—
c 2 — 7
13 . 1 2
I — c 2 ( 3 c 2 — G )
> — c 2 + G .
В результате G = J 2 c 22 to 2 ( n /2 + 2 n n — i ) 2 / T 2 п 1 . Зная c i и t c, найдем значения вращающих моментов, действующих на упругую связь 4. Для этого используем представленные ниже зависимости [6–9].
— Предохранительная фрикционная муфта (упругий вид):
T' 2 = Т п1 + CA + q^Т н . (i2)
c 2
— Предохранительная фрикционная муфта (жесткий вид):
Т" 2 = Т п1 + C 2 to \- J 2- . (I3)
-
V c i + c 2
По итогам выполненных вычислений необходимо сделать ряд замечаний. С увеличением с2 сокращается значение момента, возникающего на упругой связи 4 (упругая муфта). Если с2 растет, увеличивается и вращающий момент T"2 (жесткая муфта).
Рассмотрим типы нагрузки привода. Важно учесть, что до срабатывания предохранительной фрикционной муфты перегрузка не является причиной остановки рабочих органов машины (рис. 2).
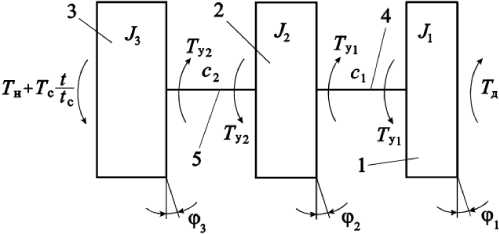
Рис. 2. Расчетная динамическая схема 2
Машиностроение и машиноведение
Уравнения для данной системы:
Лф1 + q^ — ф 2) = Т д ,
J 2 ф 2 — c 1( ф 1 -ф 2 ) + c 2( ф 2 -ф 3 ) = 0,
J 3 ф 3 — c 2 ( ф 2 -ф 3 ) = — Т н — Тс — . (16)
t c
Здесь ф1, ф2 , фз — обобщенные угловые координаты масс инерции 1, 2 и 3; Tc — значение возможного роста вращающего момента в устройстве рабочего органа; tc —время (связано со значением скорости роста перегрузки и Tc ). Значение вращающего момента Tc (зависит от типа технологической машины и возможностей ее применения) записывается в виде: (1,2...4)Tн [10–13]. Рабочий орган имеет резерв мощности, и значение угловой скорости масс инерции 1 принято неизменным, т. е. ф1 = wt. В этом случае, учитывая (16), получим [13]:
С 1 ( ф 1 -ф 2 ) = Т д .
Выполним суммирование:
Суммируем (15) и (16):
J 2 ф 2 + ( С 1 + С 2 ) ф 2 — C 1 w t — с 2 ф 3 = 0 .
J 2 ф 2 — c 1 w t + c 1 ф 2 + J 3 ф 3 = — Т н — T c T . t c
Дважды дифференцируем (16):
J 2
d 4 ф d 2 ф2
+ ( c 1 + c 2)-^
dt 4 dt 2
—
C 2 d 2 Ф з = 0. dt 2
Используя (18), получим:
d 2 ф 3 1 f t
----= —I QO t — С 1 ф 2 — Т н — T c —
J 3 V t c .
dt 2
—
J 2 d ф 2
J 3 dt 2
.
Подставим последнее выражение в (16):
d 4 ф 2 dt 4
c 2 J 2 + ( q + c 2 ) J 3 d 2 ф 2 q c 2 с 2 f „ Tt 3
+---— +-- ф 2 =----- I c 1 w t — Тн — Tc — I.
J 2 J 3 dt 2 J 2 J 3 J 2 J 3 V t c J
Из (20) находим:
ф 2 = — J 3 C 2 V
d ф 3 I m m t
—— + c 2 ф3 + Тн + Tc — dt2 tc J
Дважды дифференцируя (21), получим:
d 2ф2 1 fr d 4ф3 d 2ф3)
—Г- =— J 3—г + C2—V dt 2 C 2 ^ dt4 dt 2 J
Подставим (22) и (21) в (18):
Здесь
d4ф3 + c2J2 + (C1 + c2)J3 d2ф3 + C1C2 ф = _C2_ dt4 J2J3 dt2 J2J3 J2J3
Запишем общие решения уравнений (22) и (23):
c + c2
C 1w t —1--- 2
c 2
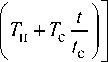
ф2 = Ax sin kyt + Bx cos kyt + Q sin k2t + A cos k^t + ~ c1 w t — Т н — Тс - , С 1 V н c t c J
Ф3 = A2 sin k1t + B2 cos k1t + C2 sin k21 + D2 cos k21 +--— с1 + с2.
C l + c 2 f _ t
C1w t I Тн + Тй — c2 V tc
.
k 1,2 =
c 2 J 2 + ( C 1 + c 2 ) J 3
C 2 J 2 + ( C 1 + C 2 ) J 3
2 J 2 J 3
2 J 2 J 3
c 1 c 2
J 2 J 3
.
Результаты исследования. Используя выражения (22) и (23), найдем значения нагрузки, возникающей в упругих связях, не представленных в (18). В этом случае используем значения движущего момента T д , равного ( ф 1 — Ф 2)( 1 ). Наличие момента Тн позволяет записать обобщенные координаты: ф 1 — ф 2 = Тн / с 1 , Ф 2 — Ф з = Т н / с 2 , Ф 1 = ю 1 . Опишем условия старта при увеличении нагрузки (от начальных показателей): при t = 0 ф 2 = — Тн / C i , d Ф 2 / dt = to ; Ф 3 = — ( С 1 + c 2 ) Тн / c 1 c 2 , d Ф 3 / dt = to . Учитывая (17) и (18) и стартовые условия, получим (при t = 0):
d 2 ф 2 = c 2 т • d 3 ф 2 =0- d 2 ф 3 = с 2 — 2 С 1 Т * d 3^3 = 0
dt 2 J 2 c 1 н dt 3 dt 2 J 3 c 1 н dt 3
Используем стартовые условия, полученные показатели и основные выражения (22) и (23). Получим значения постоянных процесса интегрирования:
A 1 = —
k 22 T c ; B T н c 2 ;
k 1 ( k 21 — k 22 ) c 1 t c c 1 J 2 ( k 21 — k 22 )
C =
k 2 1 T c
A 2 = —
k 2 ( k 1 — k 2 ) c 1 t<
k 2 2
k 1( k 2 1
—
k 22 ) X
-; D =
c
( c 1 + c 2 ) T c . ;
c 1 c 2 t c
—
T н c 2 ;
c 1 J 2( k 21 — k 22 )
B 2 = —
Т н ( c 2 — 2 c 1 ) .
c 1 J 3( k 21 — k 22 )
r _ k 21 ( c 1 + c 2 ) T c .
C 2 =---- 55— X--------- .
k 2( k 1 — k 2) c 1 c 2 t c
D 2 =
Т н ( c 2 2 c 1 )
c 1 J 3( k 21 — k 22 )
Подставим значения, полученные после интегрирования, в (22) и (23):
ф 2 =
( k 21 — k 22 ) C 1 tt c
T 1 k 1 • , — —1sin k 2 1
k
2 sin k}t + k1
. . 1 I _ T t ).
н ^c I .
_ c1 к
(Ci + c2)T k^ 1 .
—--2— с -^sin k 2 1 — —— sin k 1 t +
—
к
k 2
+ ^н c 2 (cos kt — cos k2t ) + — c to t — TH
J 2 н
Ф з = 777— 2T—
( k 1 - k 2 ) с 1
+ ( c 2 — 2 c 1 ) Т н J 3
c 2 t c
(cos k 2 t — cos k 1 t ) +
k2
к 2
c 1 + c 2
qto t —
k 1
c 1 + c 2
c 2
V
„ t
Тн + Tc - tc
.
Значения вращающих моментов, воспринимаемых упругими связями 4 и 5:
T 1 = ( ф 1 —ф 2 ) c 1 = — k 2 1
—
Tc
—н-2- (cos k 1 t — cos k 2 1 )
T 2 = ( ф 2 — ф 3 ) c 2 =
c 2
—
Tci k 1 . z ---—sin k2 t к k2
c 2 t c
k 2
k 2 1
T
-—- — —2sin kd 1sin k2t k 2 2 _ t c к k 1 1 k 2 2
k 1
k 2
л
—
V
( k 2 1 — k 22 ) C 1 _
+ T H + T c-;
t c
T I с 2 1 c 2 — 2 c 1
Т нI T+T
(cos k 1 t — cos k 2 1 ) —
k 2
---sink t k1 1
к
c 2 2
c 1 + c 2
C 1 — C 2 I _ _ t 1
to t + T + T .
нc c 1 к t c V
Значения k 1 t и k 2 t не связаны друг с другом. Значения sin k 1 t , sin k 2 t , cos k 1 t , cos k 2 t могут быть положительными или отрицательными: sin k i t = 1 и sin k 2 1 = — 1 или cos k i t = — 1 и cos k 2 t = 1 [10-12]. Значения этих временных промежутков находятся из (27):
t k + k 2
t , = ( T — Т н )f — '2 22 ,
T c k 1 k 2 ( k 1 — k 2 )
Машиностроение и машиноведение
t 2 = t- ^ Т . — 2 T c п
2 c 2
_ ( k 21 — k 22 ) J'. 2
T
н
Подставив (27) и (28) в (29), получим значения взаимосвязанных вращающих моментов в упругой связи 5 [13]:
_ ( k 31 + k 32 ) c 2
T 2 = 2
k 1 k 2 ( k 1
т
c
—
С 2 ® c i + c 2
+ ( Tn — th ) — пн
Tc c i + c 2
С 22 ® , ( c i — c 2) T c
c 1 t c
+ cxz^l T н, c1
— k 22 ) I c i t c
|
t c T о =-- 2 c |
T n |
|
+ T! |
c 1 |
^^^^^^в c2
—
2 c 2
С 22 ®
T н
( k 2 i — k 22) J 2 J |_ c i + c 2
+ ( c i — c 2 ) T c c 1 t c
+
2 c 2
c 2 , c 2 — 2 c i
c i ( k 2 i — k 22) c i I J 2
.
Используем выражение для вычисления распорной силы [13], чтобы получить максимальное значение вращающего момента, который передает предохранительная фрикционная муфта при увеличении наружного момента до T i :
F p =
T i — T' 2
r
tg a .
Используем это выражение, чтобы найти вращающий момент T' 2 :
T — T\
T 2 = R ср fl | F n — T ---2 tg a
I r
Учтем значение для полного вращающего момента T n ПФМ и получим Tn = T . Таким образом, к окончанию 2-го временного отрезка t 1 … t 2 , когда завершается распределение нагрузки в предохранительной фрикционной муфте, оказываются одинаковыми значения момента трения и наружного вращающего момента.
Обсуждение и заключения. Найдена зависимость для вычисления минимального числа пар трения основной фрикционной группы. Показано, что при этом минимуме коэффициент усиления, используемый для реализации «идеальной» нагрузочной характеристики ПФМ, не превышает предельно допустимое значение, даже если величина коэффициента трения максимальна. Представлена принципиальная модель ПФМ, в которой при минимальном значении коэффициента трения отрицательная обратная связь не действует. В принципиальной схеме модернизации базового варианта ПФМ для повышения точности срабатывания и номинальной нагрузочной способности отсутствует отрицательная обратная связь при минимальном значении коэффициента трения.
Список литературы Повышение стабильности функционирования рабочего органа в кривошипных прессах
- Брауде, В. И. Системные методы расчета грузоподъемных машин / В. И. Брауде, М. С. ТерМхитаров. - Ленинград: Машиностроение, 1985. - С. 181-205.
- Кочаев, В. П. Расчеты деталей машин конструкций на прочность и долговечность / В. П. Кочаев, Н. А. Махутов, А. П. Гусенков. - Москва: Машиностроение, 1985. - 224 с.
- Афанасьев, М. К. Исследование фрикционных муфт повышенной точности ограничения нагрузки: автореф. дис... канд. техн. наук / М. К. Афанасьев. - Киев, 1971. - 21 с.
- Муфты повышенной точности ограничения нагрузки / Я. И. Есипенко. - Киев: Технiка, 1972. - С. 168-175.
- Запорожченко, Р. М. О характеристиках предохранительных фрикционных муфт повышенной точности срабатывания / Р. М. Запорожченко // Известия высших учебных заведений. Машиностроение. - 1971. - № 1. - С. 48-52.
- Запорожченко, Р. М. К вопросу об эффективности фрикционных предохранительных муфт с точки зрения снижения веса приводов / Р. М. Запорожченко // Вестник Харьков. политехн. ин-та. - 1971. - Вып. IXIV, № 58. - С. 16-19.
- Шишкарев, М. П. Исследование точности срабатывания адаптивных фрикционных муфт с комбинированной обратной связью (часть 2)/ М. П. Шишкарев, К. О. Кобзев // Науковедение. - 2013. - № 4 (17). - Режим доступа: http://naukovedenie.ru/PDF/03tvn413.pdf (дата обращения: 28.10.2019).
- Шишкарев, М. П. Синтез принципиальной схемы модернизированного варианта адаптивной фрикционной муфты с комбинированной обратной связью/ М. П. Шишкарев, К. О. Кобзев // Инженерный вестник Дона. - 2013. - № 2. - Режим доступа: http://www.ivdon.ru/magazine/archive/n2y2013/1738 (дата обращения: 28.10.2019).
- Шишкарев, М. П. Элементы теории отрицательно-нулевой обратной связи в адаптивных фрикционных муфтах / М. П. Шишкарев, К. О. Кобзев // Вестник Донского гос. техн. ун-та. - 2014. - № 1. - C. 180- 191.
- Основы методологии расчета и проектирования адаптивных фрикционных муфт с раздельным силовым замыканием/ М. П. Шишкарев// Науковедение. - 2013. - № 5. - Режим доступа: http://www.naukovedenie.ru/PDF/17tvn513.pdf (дата обращения: 28.10.2019).
- Специфика методик расчета и проектирования адаптивных фрикционных муфт с раздельным силовым замыканием/ М. П. Шишкарев// Науковедение. - 2013. - № 5. - Режим доступа: http://www.naukovedenie.ru/PDF/18tvn513.pdf (дата обращения: 28.10.2019).
- Clutch adjustment mechanism: patent/ J. M. Chapman, T. C. Mounce; Ace Mfg & Parts Co // Justia patents. - Режим доступа: https://patents.justia.com/patent/8047351#history (дата обращения: 28.10.2019).
- Lubrication controlling method for starling clutch: patent/ Tomoyuki Miyazaki; NSK-Warner K. K. // patents.google.com. - Режим доступа: https://patents.google.com/patent/US8037990 (дата обращения: 28.10.2019).


