Повышение точности измерения температуры по тепловизионным изображениям

Для измерения температуры дистанционным методом используется микроболометрический модуль S5IR, который регистрирует тепловизионные изображения. В этом модуле используется матрица фотодетекторов типа UL03-162. Расчёт температуры базируется на теории теплового излучения абсолютно чёрного тела (АЧТ) [1]. На этапе градуировки матрицы фотодетекторов составляется градуировочная таблица, связывающая температуру и амплитуды пикселей. На этапе измерения по заданным амплитудам пикселей по градуировочной таблице отыскивается соответствующая эффективная температура АЧТ. Недостатком такого метода является использование интерполяции градуировочной таблицы, что вносит определённые погрешности измерения температуры. Повысить точность оценивания температуры с помощью тепловизора и получить статистические характеристики этих оценок в этом случае можно путём использования многоотклико-вой модели зависимости амплитуды пикселей от температуры. Возможность использования методов регрессионного анализа в задачах обработки изображений показана в работе [2].

F ( B , t ) = {f 1 ( B , t ),f 2 ( B , t ), _ ,f m ( B , t )} ^T - вектор функций зависимости амплитуды от эффективной температуры для каждого пикселя,

E = {e 1 , e ₂, ^ , e m } ^T - вектор ошибок наблюдений амплитуды.

Вектор оценок коэффициентов в общем виде рассчитывается с помощью следующей итерационной процедуры [4]:

n

B ^{1 + 1} = B ¹ + V b ¹ £ P ( B ¹ , t j ) V E ¹ [ U j - F ( B ¹ , t j! , (2) j = 1

где n – количество наблюдений температуры, V _E – ковариационная матрица ошибок наблюдений, P ( B , t ) – матрица производных по коэффициентам.

Таким образом, входными данными для метода построения модели измерения эффективной температуры служат значения задаваемых температур t j , j' = 1, n и соответствующий вектор измеренных для каждого пикселя амплитуд U j = { u 1 j , u _{2 j} , ^ , u_mj } ^T , полученный для каждой температуры.

Матрица P ( B , t ) определяется как

, . d F(B , t)

P(B , t ) = —'    ) =

( , ) dBГ a f1 ( b, t) d f2 ( b, t)       d fm ( b, t) 1

=                   ,, ^ ,.

I d B , d B , , d B I

В качестве оценки ковариационной матрицы V_E использовалась матрица S_E , которая рассчитывается по формуле [3]:

a

S E = —T 2 ( U 1 - ^U )( U 1 - ^U ) .

a ¹ 1 = 1

где a – количество точек наблюдения амплитуды, для которых температура практически не изменяется.

Ковариационная матрица оценок коэффициентов рассчитывается по формуле

V b =

n _T

2 P ( B ¹ , t j ) V E 1 P ( B ¹ , t j )

j = 1

где B – вектор оценок коэффициентов, полученных по формуле (2).

• 2.    Анализ ковариационной матрицы ошибок наблюдений и проверка адекватности модели

  • 2.1.    Методика анализа ковариационной матрицы

Исследование ковариационной матрицы ошибок наблюдений S _E состоит в оценивании элементов этой матрицы и в проверке гипотезы о некоррелированности некоторых ошибок наблюдений. Проверяется гипотеза о значимости элементов этой матрицы 5 _{E ij} ( i,j = 1, m ; i ^ j ) [4]. Для этого вычисляется коэффициент корреляции в виде

t^{s + 1} = t⁵ -ф ( В , u , t⁵ )

дф ( В , u , t⁵ ) d t

Выражение (8) было обобщено на случай вектора оценок температуры следующим образом:

T 5 + 1    T 5

д Ф ( В , T ⁵ , U ) д Т

-J

-1

Ф ( В , T ⁵ , U ) ,

sEij rij        I sEii sE jj

Если наблюдения некоррелированы, то величина % = т_ц ^ ( n - 2) / (1 - т_ц ²) имеет t -распределение, нечувствительное при n >10 к числу степеней свободы. Незначимые элементы матрицы S _E принимались равными нулю.

• 2.2.    Проверка на нулевое среднее

Для проверки гипотезы о равенстве нулю математического ожидания остатков использовалась T -статистика Хотеллинга [5] в виде

где T = { t 1 , 1 ₂, ^ , t m } ^T - вектор оценок температуры по каждому пикселю.

Векторная функция Ц ( В , T , U ) включает формулы зависимости амплитуды от температуры для каждого пикселя и имеет следующий вид:

Ф ( В , T , U ) = { ф 1 ( В , u , t ) , Ф 2 ( В , u , t ),..., ф m ( В , u , t ) } ^T .

Ковариационная матрица V_T оценок температур по всем пикселям равна

V_T = AV_rA ^t + GS_rG^T ,                    (10)

TBE

где A = A , - A ₂, G = G 1 - G ₂,

T ²

nm - к

n

Z RTSrRj j=1

A =

_ . ,               x -I T Г — . z дФ( В, T, U) дФ( В, T,U)

- 1

где R = U - F ( B , t ) - вектор остатков модели, а матрица S _E рассчитывалась по формуле (3).

Если остатки имеют нулевое математическое ожидание, то статистика (6) приблизительно имеет распределение Фишера со степенями свободы f 1 = n - к / m и f , = a - 1.

Тогда при выполнении неравенства

д В

д Т

,

A 2 = Ф ( В , T , U ) ^T

д Ф ( В , T , U ) 1 ^{- 2} д ² Ф ( В , T , U ) д T          д Т д В

G =

д Ф ( В , T , U ) T Г д Ф ( В , T , U ) d U           д Т

G 2 = Ф ( В , T , U ) ^T

- 1

д Ф ( В , T , U ) 1 - 2 д ' Ф ( В .Т. и ) д т         o t o u

Т ²

T < 'j1,f>,1-« где Ff1,f2i1-K - квантиль распределения Фишера со степенями свободы f1 и f2 на уровне значимости а, гипотеза о равенстве нулю математического ожидания остатков принимается с доверительной вероятностью 1 -а.

• 3.    Расчёт оценки температуры по вектору амплитуд

В качестве метода расчёта температуры использовался метод Ньютона [4], который основан на линеаризации целевой функции ф ( B , u , t ) = u - f ( В , t ) в окрестности точки t * в виде:

_ч дф( B , u , t *), ..

ф ( В , u , t ) + — Ц---- Ч t - t ) = 0,              (7)

о t дф(В,u,t)

где --------- - производная функции ф (В, u, t) по д t температуре.

Тогда итерационная процедура расчёта оценки температуры принимает следующий вид:

Общая оценка температуры t минимизирует квадратичную форму (Jt - T)T V,1 (Jt -T), где J - вектор размерности m, элементы которого равны единице, Т - вектор частных оценок температуры по каждому пикселю, которые рассчитываются по формуле (9). Приравнивая производную от этого выражения по t нулю, получим оценку температуры t в виде:

? = ( J ^T V_T ^{- 1} J )^{- 1} J ^T у-Л .                         (11)

Дисперсия 5 2 оценки t (11) равна

5 t ² = ( J ^T VJ )^{- 1} ,                                 (12)

что меньше наименьшей из дисперсий частных оценок.

При независимых оценках Т , т. е. когда ковариационная матрица V T является диагональной матрицей, выражение (11) приводит к известной формуле для неравноточных наблюдений.

• 4.    Анализ результатов эксперимента

Экспериментальные данные получают путём регистрации излучения от АЧТ в диапазоне температур, максимально приближенных к рабочему (0-150°C). Последовательно проводились n =26 наблюдений с различными значениями установленной температуры АЧТ ti, в процессе которых регистрировались и сохранялись тепловизионные изображения АЧТ. Каждое изображение представляется матрицей амплитуд пикселей, общее количество пикселей равно 384x288 = 110592 пикселей.

Точки для расчёта ковариационной матрицы S E (3) значения a <  n выбирались при низких температурах, где зависимость f i ( B , t ) ( i = 1, m ) на начальном участке хорошо описывается линейной функцией (рис. 1). Таким образом, матрица S E рассчитывалась как ковариационная матрица остатков линейной по t модели, построенной по участку низкотемпературных данных (0-20) ° С. Структура этой матрицы имеет следующий вид: дисперсии ошибок наблюдений откликов пикселей равны 78–86 (в относительных единицах), а коэффициенты корреляции (5) равны 0,95–0,98.

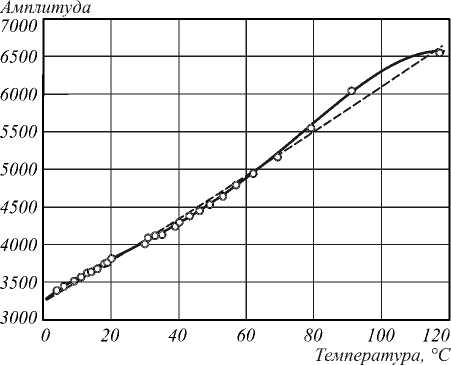
Рис. 1. Зависимость амплитуды пикселя от эффективной температуры для полиномиальной модели (сплошная линия) и модели АЧТ (пунктирная линия)

В [1] показано, что зависимость амплитуды u пикселя, формируемого ИК камерой, от температуры АЧТ описывается формулой:

и =----^b ------,                      (13)

exp( b 2 + 273) - 1

где t - температура чёрного тела ( ° C), B = { b 1 , b ₂} T -вектор коэффициентов, зависящих от используемого объектива, его относительного отверстия и фильтров камеры. Кроме этой модели, исследовались полиномиальные модели: линейная, квадратичная, полиномы третьей и четвёртой степени. Расчёты оценок коэффициентов модели (1) выполнялись по формуле (2).

Для каждой модели рассчитывалась величина путём решения уравнения

T 2 = f f 2 , p ,                                   (14)

где F_{f 1, f 2, P} – квантиль распределения Фишера для вероятности P .

Для модели АЧТ (13) получены расчётные значения T ² = 11,16 (6), что для числа степеней свободы f ₁ = 22 и f ₂ = 5 соответствует P = 0,993 (14); такая модель принимается неадекватной на уровне значимости более 0,007.

Для модели в виде полинома четвёртой степени значение статистики (6) T ² = 2,37, что соответствует P = 0,828; это недостаточно для признания этой статистики значимой на уровне значимости менее 0,172. Следовательно, дисперсии S E (3) и V R (7) считаются одинаковыми и гипотеза о равенстве нулю математического ожидания остатков принимается, т. е. модель следует признать адекватной. Типичное положение экспериментальных точек для одного пикселя и построенные модели показаны на рис. 1.

В результате использования формул (11,12) относительная погрешность расчёта температуры s_t / t ˆ составила около 0,015%.

Высокие значения ковариаций в матрице S E приводят к существенному повышению дисперсии оценки t ˆ по сравнению с диагональной матрицей. Для диагональной матрицы S E относительная погрешность составляет 0,005%.

Для сравнения были проведены расчёты оценки температуры с использованием кусочно-линейной интерполяции для каждого отдельного пикселя с последующим усреднением частных оценок. Относительная погрешность расчёта температуры в этом случае составила приблизительно 0,045%.

Выводы

Использование многооткликовых регрессионных моделей для описания зависимости амплитуды пикселей тепловизионного изображения от температуры позволяет учесть корреляционные связи ошибок наблюдений откликов пикселей, что повышает объективность и точность метода расчёта температуры.