Повышение точности локализации источников дискретных составляющих спектра шума движущегося транспортного средства

Электронный журнал «Техническая акустика»

На сегодняшний день основным методом локализации мест излучения тональных сигналов на движущемся транспортном средстве при использовании одноточечного приема является метод компенсации эффекта Доплера. Данный метод заключается в компенсации фазовых искажений, обусловленных движением источника относительно неподвижного приемника [1, 2]. Эффект Доплера приводит к сжатию/растяжению принимаемого сигнала вдоль оси времени. Численная мера такого (мультипликативного) искажения выражается коэффициентом Доплера в виде:

Kd = vs Iva ,                                                                                        (1)

где v_s — скорость сближения/удаления приемника по отношению к источнику, v_a — скорость звука.

При излучении сигнала с постоянной частотой это приводит к изменению во времени частоты принимаемого сигнала по отношению к частоте опорного. Для компенсации такого изменения приемник сигнала может содержать схему фазовой автоподстройки частоты (ФАПЧ) или функцию, выполняющую повторную дискретизацию (ПД) принимаемого сигнала, учитывающую меру сжатия/растяжения сигнала. При использовании цифрового представления сигнала компенсацию эффекта Доплера производят путем перераспределения цифровых отсчетов сигнала по временной шкале [1-3].

В данной работе предлагается определять место излучения квазигармонического сигнала, используя преобразование временного масштаба и компенсируя амплитудные искажения сигнала, а в роли критерия качества компенсации использовать сравнение автокорреляционных функций получаемых при этом сигналов.

При прямолинейном равномерном движении источника принимаемый сигнал S_np ( t ) будет модулирован по амплитуде и по фазе из-за эффекта Доплера

S пр ⁽ t ) =

S (t ')

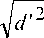
+ v ' 2 ( t '— 1 0 ) 2

где d ' — минимальное (траверзное) расстояние между источником и приемником; v ' — скорость движения источника; 1 0 — момент времени достижения траверза; t' — момент времени, определяемый из уравнения c ( t - 1 ') = R ( t '), в котором с — скорость распространения сигнала в среде, R ( t ') — текущее расстояние от источника до приемника:

R ( t ' ) = dd '² + v '² ( t '- 1 о ) (в первом приближении полагают t' = t - R ( t )/ c ). (3)

В рассматриваемом случае стационаризация принятого сигнала S_np ( t ) осуществляется путем умножения отсчетов сигнала на множитель R ( t ) и переносом отсчетов по временной шкале [4].

Параметрами стационаризирующего преобразования будут v , d , t 0 , и, поскольку вид нестационарности S_np ( t ) заранее известен и описывается формулой (2), здесь можно говорить о согласованной стационаризации сигнала, при этом в точке стационарности будет v = v' , d = d' , 1 ₀ = t ‘ . Естественно ожидать, что в точке стационарности время когерентности, т кт , максимально. Для поиска такого максимума выполняется стационаризация сигнала S_np ( t ) при значениях v = v' , d = d' и различных значениях 1 ₀ .

Физически это соответствует перебору значений момента времени, в который источник находился на минимальном (траверзном) расстоянии от приемника, то есть рассматривается задача о локализации места излучения сигнала, при этом обязательно решается вопрос о критерии, по которому оценивается результат локализации и ее точность.

В отличие от метода локализации мест излучения дискретной составляющей спектра (ДСС) сигнала предложенного в работе [2], где авторами статьи предлагалось определять места излучения по совокупности спектров мощности сигналов, представляемой как пространственно-частотное изображение в координатах «частота-линейная координата», в данной статье предлагается определять места излучения по зависимости времени когерентности стационаризированного сигнала от линейной координаты. Временем когерентности будем считать интервал времени, на котором вероятность идентификации участка автокорреляционной функции как гармонического колебания по критерию Колмогорова-Смирнова не меньше, чем е-1.

В предлагаемой процедуре производится сравнение автокорреляционных функций изучаемого процесса и гармонического колебания со случайной начальной фазой При этом следует учесть три важных момента:

• -    временная длительность Т фрагмента изучаемого процесса конечна, следовательно, его автокорреляционная функция будет содержать случайные флуктуации;

• -    анализируемый процесс всегда занимает конечную полосу частот Д / в которой и ищется дискретная составляющая;

• -    анализируемый процесс может быть нестационарным, то есть, частота и амплитуда искомого квазигармонического колебания могут медленно изменяться со временем, в том числе и периодически.

Из сказанного следует, что измеряемая автокорреляционная функция анализируемого процесса также содержит в себе случайные составляющие, и ее сравнение с эталонной автокорреляционной функцией гармонического колебания должно выполняться с использованием статистических критериев.

Сравнение двух указанных автокорреляционных функций может выполняться по их различным характеристикам. Часто применяется сравнение фактического значения автокорреляционной функции с уровнем флуктуаций, рассчитанным для автокорреляционной функции 5-коррелированного процесса, пропущенного через полосовой фильтр шириной Д/. Процедура такого сравнения поясняется рисунком 1, где приведены графики огибающих нормированных автокорреляционных функций Р ( ^{т )} [6].

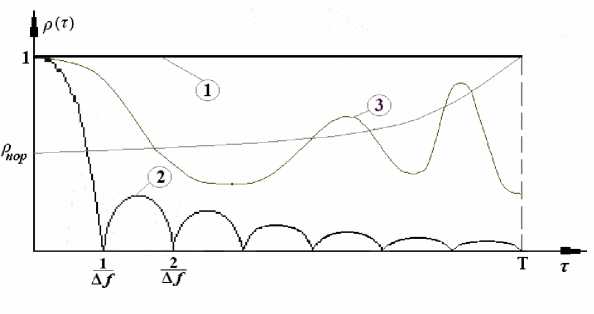
Рис. 1. Огибающие автокорреляционных функций гармонического (1), шумового (2) сигналов и их смеси (3)

При сравнении значений автокорреляционных функций следует учитывать, что кривая (2) на рисунке 1 испытывает относительные флуктуации амплитуды σ _фл ≈ 1 I л/∆ f ( T - τ ) , и о превышении над уровнем этих флуктуаций судят по превышению значений нормированной автокорреляционной функции ρ ( τ ) исследуемого процесса р ( t ) над установленным пороговым значением

ρ _пор = βσ _фл , (4) в котором β выбирается в зависимости от заданной вероятности идентификации исследуемого процесса, как гармонического.

• У такого подхода можно отметить два главных недостатка:

  – строго говоря, превышение значения ρ ( τ ) над ρ пор означает лишь похожесть фрагментов временных реализаций процесса при сдвиге на время τ , но не гармонический характер этого процесса;

  – превышение значения ρ ( τ ) над ρ пор при некотором значении τ ничего не говорит о временном интервале τ ког , на котором можно считать фрагменты похожими или когерентными, то есть важный вопрос о естественной ширине дискретной составляющей спектра ∆ f е остается открытым.

Иной подход к определению квазигармонической составляющей в случайном сигнале состоит в том, чтобы сравнить не огибающие, а фрагменты нормированных автокорреляционных функций гармонического колебания со случайной начальной фазой и исследуемого сигнала, причем для сравнения можно выбирать фрагмент, последовательно изменяя его длительность и положение в реализации автокорреляционной функции (рисунки 2–5).

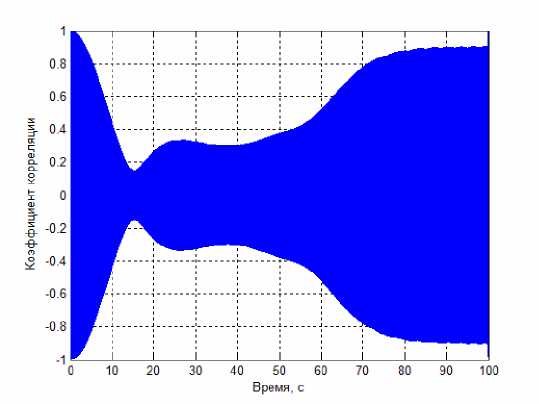
Рис. 2. Автокорреляционная функция нестационаризованного сигнала

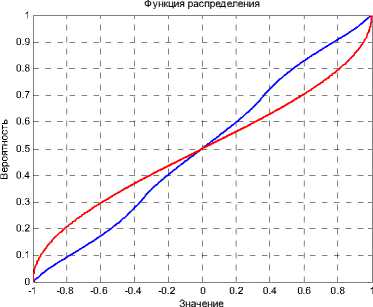
О 10    20    30    40     50    60    70    80    90    100

Время, с

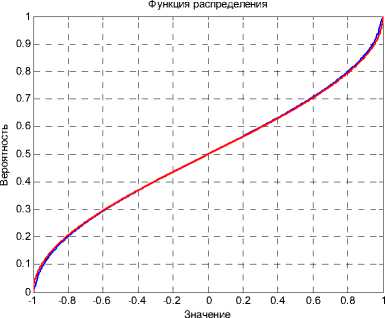
Рис. 3.

Функция распределения значений автокорреляционных функций: а) гармонического сигнала, б) нестационаризованного сигнала

Рис. 4.

Автокорреляционная функция почти стационаризованного сигнала

Рис. 5.

Функция распределения значений автокорреляционной функции почти стационаризованного сигнала

Максимальная длительность фрагмента, соответствующего гармоническому колебанию, будет давать значение времени когерентности процесса τког. Степень соответствия фрагмента автокорреляционной функции исследуемого сигнала гармоническому колебанию можно получить, если сравнить функции распределения вероятностей значений этих двух автокорреляционных функций в пределах фрагмента. Понятно, что для гармонического колебания со случайной начальной фазой автокорреляционная функция ρ0(τ) имеет вид ро(т) = cos^Т ,

в котором в выбирается в зависимости от заданной вероятности идентификации исследуемого процесса, как гармонического, а её функция распределения —

. э. Л 1 1

.

F„ ( x ) = — +—arcsin x ^{р 0} I 2 п

Для исследуемого процесса функцию распределения вероятностей значений р ( т ) на выбранном фрагменте длительностью А т обозначим F^x,АТ). Сравнение функций F _p ( x,АТ) и F p 0 ( x ) проведем по двустороннему критерию Колмогорова-Смирнова [4, 5], применяемому для проверки непараметрической гипотезы о равенстве двух функций распределения. При выполнении этой процедуры [7] для каждого фрагмента автокорреляционной функции р ( Т ) длительностью А Т получается значение вероятности Р _р (т, Ат ) = P { F _p ( x , А т )~ F P ^Э _о ( x ) } , с которой функции F _p ( x, А т ) и F p ( x ) можно считать неразличимыми, то есть распределение значений фрагмента автокорреляционной функции исследуемого сигнала такое же, как и у гармонического сигнала со случайной начальной фазой. Изменяя время начала фрагмента т , можно выбрать фрагмент, для которого значение Р _р ( т , А т ) максимально, затем, увеличив длительность искомого фрагмента А т , повторить процедуру его поиска, добиваясь максимального значения вероятности Р _р ( т , А т ). При такой итерационной процедуре следует установить начальные значения А т и Р _р ( т , А т ). Очевидно, что

Ат > —, Af где Af — полоса частот, в которой рассматривается процесс, а

Р р (т,АТ) >  Р кр . (8)

При этом критическое значение вероятности Р кр выбирается на уровне 1/е, что может трактоваться, как пороговое значение когерентности процесса, которое часто в физических исследованиях принимается равным е ^-1.

Выполняя описанную процедуру, можно найти в реализации р ( т ) фрагмент максимальной длительности при вероятности, превышающей пороговое значение. Это значение длительности фрагмента можно выбрать в качестве времени внутренней когерентности процесса

т ког

= max А т .

р >р

• ¹    р >  кр

Построив зависимость времени когерентности от координат точки компенсации нестационарностей, обусловленных относительным движением приемника и источника (формула (2)), можно определить предполагаемое местоположение источника ДСС. На рисунках 6 и 7 представлены зависимость времени когерентности от координаты и изображение в координатах «частота-линейная координата» соответственно, для модельного сигнала ДСС, источник которого расположен в нуле.

Как видно из рисунков 6 и 8, при сравнительном анализе автокорреляционных функций сигналов с применением статистического критерия качества локализации точность определения места излучения ДСС увеличивается в несколько раз.

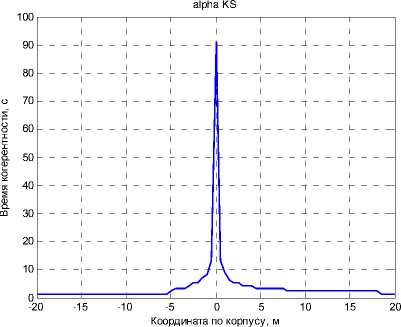
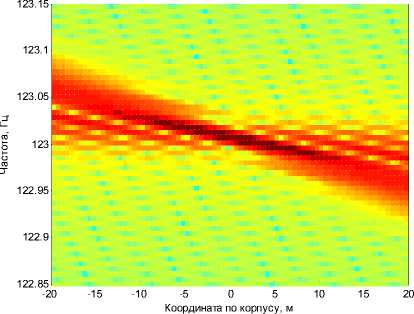
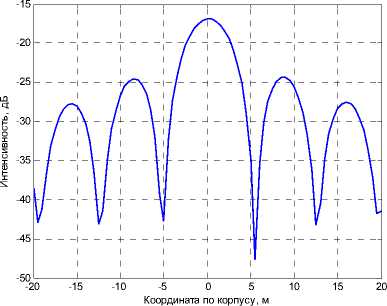
Рис. 6.

Зависимость времени когерентности от координаты

Рис. 7.

Локализация источника методом компенсации эффекта Доплера

Рис. 8.

«Разрез» на частоте максимума