Повышение точности механообработки на основе совместного численного геометрического и физического моделирования

Е.И. Щурова, , И.А. Щуров, , Южно-Уральский государственный университет, Челябинск, Россия

Мотивация и предмет исследования. Технологическая подготовка машиностроительного производства включает в себя в числе прочего разработку технологических операций, в том числе обработку на станках с ЧПУ. Наибольшие трудности возникают при обработке крупногабаритных нежестких деталей, таких как турбинные лопатки. По данным компании Sandvik Coromant прогиб лопатки во время фрезерования может достигать 2 мм, что существенно сказывается на точности обработки. Кроме того, путь резания (здесь и далее термины по ГОСТ 2576283) при фрезеровании крупных лопаток на чистовой операции достигает десятков метров, что при обработке одной заготовки приводит к значительному износу фрезы и изменению ее производящих размеров. Этот износ также сказывается на точности обработки. Минимизировать влияние на точность детали данных технологических факторов позволяет внесение корректоров в управляющую программу на соответствующих участках траектории движения инструмента. Величины корректоров должны быть определены с учетом указанных прогибов и износа инструмента в выбранных точках траектории его движения. С этой целью необходимо рассчитать силы резания, что в современных условиях наиболее адекватно реализуется численными сеточными и бессеточными методами моделирования, реализуемыми с использованием коммерческих CAE-программ [1]. Как известно, силы резания и сам характер напряженно-деформированного состояния зоны резания и стружкообразования существенно зависят от состояния поверхности заготовки, ее шероховатости и износа инструмента. Между тем применяемые в настоящее время CAD-программы, основанные на аналитической геометрии в пространстве, как правило, позволяют получать гладкие поверхности, гладкие линии их пересечения и точечные вершины моделируемых объектов. Известны примеры моделирования шероховатости поверхностей с использованием волнистых гладких поверхностей на основе сплайнов или тех же самых канонических поверхностей. Таким же образом в проводимых исследованиях моделируются и поверхности износа инструментов [2]. Очевидно, что данное моделирование не адекватно реальным поверхностям. Кроме того, в случае использования встроенных в CAE-системы генераторов сеток в этом случае создаются объемные по числу узлов и элементов модели, которые трудно реализуемы на персональных компьютерах инженеров-технологов промышленных предприятий.

Одним из перспективных вариантов преодоления указанных трудностей является отказ от аналитических твердотельных моделей и использование их численных аналогов. Основой для такого моделирования является воксельное моделирование, широко применяемое не только в компьютерных играх и медицине, но и в технике. Достоинством этого подхода является его основа – алгебра множеств, которая выгодно отличается от аналитической геометрии устойчивостью в получении результатов для сколь угодно сложных условий, включающих не только геометрию поверхностей инструментов и заготовок, но и их шероховатости, дефекты и износ. Другим достоинством этого подхода является его численная основа, которая полностью сопрягается с основой численного физического моделирования: сеточных и бессеточных методов расчета, применяемых в CAE-системах, что позволяет сократить размеры моделей. В связи с этим во-ксельное моделирование часто отражается в научных публикациях, посвященных в том числе и решению геометрических задач обработки на станках с ЧПУ, а также влиянию деформаций и износа на точность обработки. Анализ литературы показал, что в настоящее время такие задачи решаются по отдельности: только идеальное формообразование (без учета технологических факторов), например, расчет высоты остаточных гребешков шероховатости; учет влияния сил резания и деформаций на точность обработки; учет влияния износа инструмента на точность обработки (только геометрическая постановка). Необходим комплексный подход учета совместного влияния всех указанных и других факторов, таких как погрешности инструментов, погрешности закрепления заготовки, погрешности формообразующего движения на точность обработки. В связи с этим была выдвинута гипотеза о том, что подобное моделирование возможно только на основе комплексного подхода взаимосвязанных модулей CAD/CAM/CAE-систем, базирующихся на общей численной основе: воксельном моделировании геометрии и сеточных и бессеточных методах расчета при решении физических задач. Геометрическое моделирование инструментов и заготовок должно выполняться с учетом их шероховатости и износа, которые должны учитываться, например, в конечно-элементных (МКЭ) или SPH-моделях силовых расчетов, которые, в свою очередь, являются основой для расчета удаляемых с инструмента вокселей как результата его износа в зависимости от пути резания и давлений на его конечные элементы или SPH-частицы со стороны заготовки и стружки. Указанная взаимосвязь и является основой термина «совместное геометрическое и физическое моделирование» элементов технологической системы и процессов резания. Именно данный подход, связанные с ним методологические вопросы и математические модели и является предметом рассматриваемого исследования .

Методологическая база и математические модели исследования

Отмеченный выше комплексный подход требует создания своей методологической базы: требуется наличие базовых понятий, принципов и правил моделирования. Основная часть этой методологии была разработана ранее и представлена в одной из публикаций [3]. Вместе с тем ряд терминов требует уточнения. В частности, было уточнено понятие вокселя, параметр состояния которого теперь содержит в себе не только номер части моделируемого объекта или номера его поверхностей, но и его номер в октодереве всей модели. Уточнены принципы, касающиеся не только моделирования поверхностей элементов технологической системы, но и шероховатостей поверхностей и их износа.

Разработанные математические модели позволяют описывать геометрию шероховатостей разных видов для разных поверхностей. Часть результатов такого моделирования для поверхностей вращения показана на рис. 1. Выступы шероховатости для наглядности показаны с увеличенными шагами.

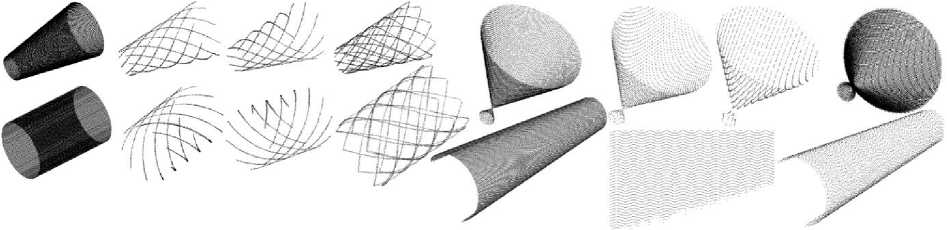
Рис. 1. Узловые точки вокселей поверхностей вращения и выступов шероховатости

Fig. 1. Nodal points on the surfaces of revolution of voxels and roughness protuberances

Аналогичные математические воксельные модели были получены для режущего клина инструмента с типичными характерами износа (рис. 2). Слева приведен пример износа реального резца, в середине - его воксельный аналог (цветами на основе значений параметров состояний вокселей выделены различные поверхности режущего клина), далее показаны результаты расчета напряжений в клине от силы резания.

Рис. 2. Изношенный участок режущего клина реального инструмента, его воксельный аналог и напряжения от силы резания. Справа – модель композитной лопатки

Fig. 2. Worn section of a cutting wedge from a real tool and its voxel analog, as well as stresses from cutting forces. On the right, there is a model of composite blade

Также была разработана математическая модель волоконно-армированной структуры объемного плетения (ортогональное расположение волокон) для заполнения ею пространства, описываемого твердотельным CAD-моделированием деталей любой формы. Результаты работы компьютерной программы на основе данной математической модели показаны на рис. 2 справа. Для наглядности размеры волокон и их граничных слоев в матрице увеличены на порядки. Данная деталь позволяет в выбранных точках ее обработки фрезой вырезать небольшие фрагменты прямоугольной формы для моделирования резания вышеприведенными фрагментами изношенного режущего клина с шероховатостью его передней и задних поверхностей. Необходимость такой композитной модели связана с различным расположением волокон по отношению к инструменту в различных точках обработки заготовки, что существенно влияет на картины напряженно-деформированного состояния зоны резания, характер стружкообразования и возникающих сил резания. Далее, как было показано выше, эти силы используются для расчета деформаций заготовки, при этом в случае заготовок больших размеров данные расчеты выполняются в CAE-программах для гомогенных анизотропных композитных структур по существующим моделям материалов. В ходе исследования были получены и другие математические модели, о которых было сказано во Введении. Перечисленные вопросы нашли свое отражение в подготовленных статьях, направленных в научные журналы.

Выводы

• 1.    Выполненные исследования являются начальным шагом в решении комплексного вопроса, связанного с созданием нового поколения CAD/CAM/CAE-систем, основанных на численных методах расчета: совместном использовании геометрического (воксельного) и физического (МКЭ или SPH) типов моделирования.

• 2.    Доказано, что модели тел – элементов технологической системы – адекватно отражают их поверхности, включая шероховатость и износ.

• 3.    Физическое моделирование контакта тел с использованием идеальных поверхностей и кромок количественно и качественно отличается от такого моделирования тел с шероховатостью и износом.

• 4.    Предлагаемый подход является достаточным для решения комплекса задач в заявленной выше постановке.