Повышение точности позиционирования системы ГЛОНАСС

Одной из основных характеристик глобальной навигационной спутниковой системы ГЛОНАСС является точность оценки координат и высоты, полученных в навигационной аппаратуре потребителей (НАП) только по спутниковым сигналам без привлечения дополнительной информации [1]. Особое значение точность позиционирования имеет для навигационных комплексов летательных аппаратов, в том числе беспилотных, в условиях непреднамеренных и умышленных помех [2; 3]. Однако недостаточная во многих случаях точность позиционирования требует разработки других способов решения этой задачи. В работе [4] предложено использовать для решения фундаментальных геодинамических и геодезических задач систему высокоточного определения эфемерид и временных поправок, осуществляющую сбор, хранение и обработку измерительной и навигационной информации по спутниковым навигационным системам ГЛОНАСС. В [5] предложены расчетные способы снижения ошибок, обусловленных прохождением сигнала в ионосфере и тропосфере, в [6] показано, что применение методов пространственной селекции с помощью антенной решетки позволяет существенно повысить точность навигационных определений за счет уменьшения влияния многолучевого приема. В работе [7] описана идея цифровой регистрации навигационных сигналов и предложен метод высокоскоростной постобработки для повышения точности оценок. Подход к повышению помехоустойчивости навигационной аппаратуры за счет использования схемы глубокого комплек-сирования навигационной аппаратуры предложен в работах [8; 9]. Способ повышения помехоустойчивости систем позиционирования путем передачи дополнительной метки времени рассмотрен в [10]. Наиболее сложным и затратным является предложенное в [11] создание новой навигационно-информационной спутниковой системы, устраняющей проблемы в развитии системы ГЛОНАСС. Большое влияние на точность позиционирования оказывают характеристики НАП. Стандартные образцы НАП не обеспечивают необходимый уровень помехоустойчивости при существующем уровне мощности принимаемых сигналов ГЛОНАСС порядка минус 166– 156 дБВт [12; 13]. В системе ГЛОНАСС для повышения помехоустойчивости используется код Хэмминга, исправляющий однократные ошибки. Передаваемые блоки цифровой информации представляет собой 85-разрядный код, в котором старшие 77 разрядов содержат информационные символы, а младшие 8 разрядов – проверочные [12].

Постановка задачи

Точность измерения координат определяется количеством спутников, одновременно видимых навигационным оборудованием. Ошибки ГЛОНАСС составляют 3–6 м при использовании 7–8 спутников. На большей части поверхности земли над горизонтом находятся одновременно до 11 спутников ГЛОНАСС, однако отношение сигнал/шум в канале связи, необходимое для безошибочного приема информации, часто обеспечивается только для 2–4 спутников. На рис. 1 показан пример видимости спутников разных систем навигации в условиях городской застройки.

На рис. 2 показаны уровни сигналов для видимых спутников.

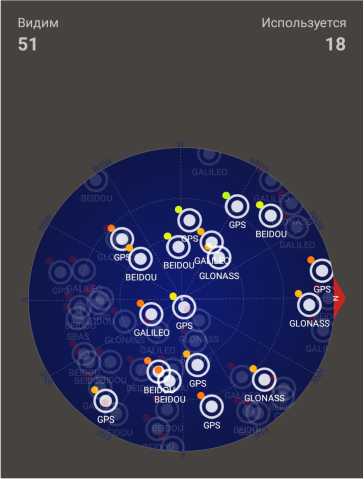
Рис. 1. Видимость спутников GPS, GLONASS, BEIDOU, GALILEO

136 {$>

27 <£

24 <$

18 ^

6 $

20 О

14 <£

7 О

4 $

34 $

3 $

9 Ф

1 О

36 ф

Тип

GLONASS

BEIDOU

GLONASS

GLONASS

GLONASS

GALILEO

BEIDOU

SBAS

GPS

GPS

GPS

GLONASS

GLONASS

GLONASS

GLONASS

GLONASS

GALILEO

GALILEO

GALILEO

GALILEO

GALILEO

Рис. 2. Видимые и используемые спутники

Fig. 2. Visible and used satellites

Fig. 1. Visibility of GPS, GLONASS, BEIDOU, GALILEO satellites

Требуемое отношение сигнал/шум выдерживается для 4 спутников ГЛОНАСС, 5 спутников ГЛОНАСС находятся в зоне видимости, но не используются из-за низкого отношения сиг-нал/шум. В этих условиях погрешность позиционирования превышает 10 м. Уменьшить погрешность позиционирования можно не только увеличением числа спутников в спутниковой группировке, но и применением кодирования, обеспечивающего исправление большего числа ошибок.

К настоящему времени разработано большое количество корректирующих кодов различной эффективности. Однако их эффективность оказывается недостаточной для восстановления исходного сообщения при передаче информации по спутниковому каналу связи в условиях низкого отношения сигнал/шум, когда могут быть утрачены большие фрагменты информации. Одним из способов повышения устойчивости канала связи является использование формы представления сигнала, обеспечивающей восстановление сообщения по его фрагменту. Такой особенностью обладает голографический способ корректирующего кодирования [14; 15]. Голографический код может быть использован для решения самых разных задач, например, для повышения надежности бортовых систем памяти [16] или повышения помехозащищенности радиолокационного канала [17]. С таким же успехом голографическое кодирование может быть применено для повышения помехоустойчивости спутникового канала связи. Процесс кодирования передаваемой информации представляет собой математическое моделирование цифровой голограммы, создаваемой в виртуальном пространстве волной от кодируемого объекта [18; 19]. Голографическое кодирование произвольной цифровой информации отличается от оптической голографии следующими факторами:

• –    объект является одномерным;

• –    объект не привязан к пространственным измерениям, единица измерения размера объекта и голограммы – длина волны излучения;

• –    волна распространяется без затухания и когерентна на любой длине.

Алгоритм голографического кодирования/декодирования

Входной блок данных исходного цифрового сообщения, представляющий собой n -разрядный двоичный код, преобразуется во вторичный блок – единичный позиционный код с числом позиций N = 2 ⁿ . Этим преобразованием в сообщение закладывается избыточность с коэффициентом q = 2 ⁿ / n . Вторичный блок имеет ( N –1) нулей и одну единицу в позиции, заданной первичным блоком. Таким образом, блок исходного цифрового сообщения используется как адрес позиции единицы в последовательности нулей единичного позиционного кода вторичного блока.

Формирование кодовой комбинации проводится путем геометрического построения в плоскости.

Из первичного n-разрядного блока данных X формируется вторичный блок A – пространственный одномерный объект (далее – объект), состоящий из точек A ( i ), i = 1… N , значение одной из которых равно 1, остальных – нули: A ( x ) = A ( i ) = 1 при i = X , A ( i ) = 0 при i ≠ X .

Расстояние между точками равно d. Ячейка A(x) является источником сферической волны, распространяющейся в плоскости анализа и характеризуемой длиной волны λ = d .

Рассмотрим значения сферического волнового фронта в плоскости нахождения объекта на линии, расположенной параллельной объекту на расстоянии L , в N точках с шагом d . Волна от источника распространяется без затухания и попадает на все элементы одномерного массива H ( j ), j = 1… N (рис. 3). Эта совокупность точек образует срез зонной пластинки Френеля (зонную линейку Френеля), которая представляет собой простейшую голограмму – голограмму точки. Таким образом, одномерному объекту A ( i ) ставится в соответствие одномерная голограмма H ( j ). Значения полученной голограммы округляются до одного бита, в результате чего формируется N -битный одномерный массив H_O ( j ), представляющий из себя кодовую комбинацию n -разрядного входного блока данных X .

Значения волнового фронта в рассматриваемых точках H ( j ), j = 1… N определяются фазой приходящей волны. Фаза волны φ является функцией пространственных координат. Значение волны от элемента A ( i ) в точке нахождения элемента голограммы H ( j ) равно

H ( j ) = A ( i )sin φ( i , j ),                                         (1)

где φ( i , j ) – фаза излучения элемента A ( i ) в точке H ( j ).

Расстояние l(i, j) между точками A(i) и H(j) равно l (i, j) = 7L + d2(i - j)2, тогда φ(i, j) – это дробная часть отношения l(i, j) к длине волны:

φ( i , j ) = {l( i , j ) / λ}.

Таким образом, кодовая комбинация H O ( j ) – это голограмма точки, она же одномерная зонная линейка, несущая информацию из входного блока данных в виде N -разрядного кода координаты центра зон Френеля.

Кодовая комбинация передается по каналу связи и на приемной стороне производится декодирование – восстановление голограммы, поиск максимума и выдача его координаты в виде n -разрядного выходного кода.

Принятая по каналу связи искаженная голограмма H R ( j ) рассматривается как одномерный массив точек, число которых может быть меньше N вследствие потери части информации, а значения принятых элементов искажены шумом. Каждая из точек голограммы H R ( j ) является источником сферической волны с той же длиной волны λ, как и при кодировании. Восстанавливаемый объект A R ( i ) представляет собой одномерный массив точек, расположенных с шагом d на прямой, параллельной голограмме H R ( j ) и расположенной на расстоянии L от нее.

Интенсивность волны от точки голограммы HR(j) в точке восстанавливаемого объекта AR(i) вычисляется так же, как и при кодировании (1). В каждую точку объекта AR(i) приходят волны от каждой точки голограммы HR(j) (рис. 3), и в результате интерференции этих волн формируются значения N-разрядного представления восстановленного объекта AR(i):

A r ( i ) = E N = 1 H r ( J ), i = 1 - N •

Таким образом, восстановленный объект A R ( i ) является голограммой второго порядка (голограммой голограммы) исходного объекта.

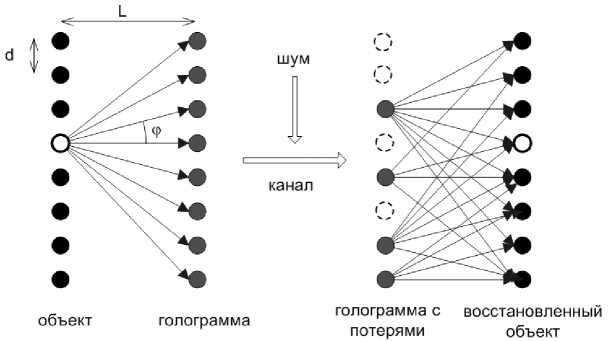
Рис. 3. Пространственная схема кодирования

• Fig. 3. Spatial coding scheme

Для получения выходного блока данных в форме n -разрядного кода необходимо определить номер позиции Y , в которой находится максимум массива A_R ( i ). Этот номер и есть значение выходного блока данных.

Последовательность операций алгоритма кодирования / декодирования:

• 1.    Преобразование первичного блока данных X во вторичный блок A .

• 2.    Расчет значений волнового фронта в точках голограммы H .

• 3.    Передача голограммы.

• 4.    Расчет восстановленного объекта A_R по принятой голограмме H_R .

• 5.    Поиск максимума в массиве A_R .

• 6.    Определение значения максимума и формирование выходного блока Y .

Результаты моделирования

Исследование помехоустойчивости рассмотренного голографического кода проведено путем моделирования в среде Matlab процессов кодирования-декодирования при передаче кодовых сообщений по каналу с шумом. В качестве источника шума использован генератор псевдослучайного шума, реализованный функцией Random.

На рис. 4 приведен результат восстановления сигнала, несущего значение Y = 100. В восстановленном сигнале присутствует небольшой шум кодирования.

Уровень шума кодирования, который определяет потенциальную помехоустойчивость кода, зависит от длины кодовой комбинации. Форма восстановленного сигнала, несущего значение Y = 400, при N = 1024 (коэффициент избыточности q = 128) приведена на рис. 5.

Рассмотрим устойчивость кода к ошибкам, вызванным шумом в канале связи. Воздействие шума смоделировано путем замены части голограммы двоичной случайной последовательностью. При длине случайного фрагмента в сигнале 70 % восстановленный сигнал превышает максимальное значение выброса шума на 11 дБ (рис. 6).

Увеличение длины кодовой комбинации приводит к возрастанию помехоустойчивости кода. При N = 1024 выходной сигнал восстанавливается из сигнала, на 80 % состоящего из случайной последовательности. Отношение сигнала к шумовому пику на выходе декодера равно 6,3 дБ (рис. 7).

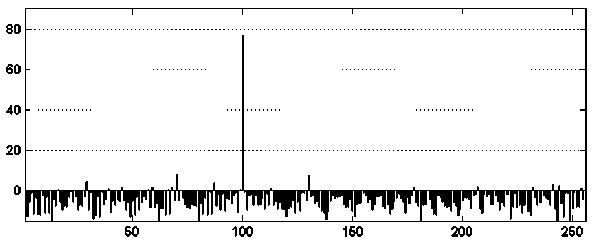
Рис. 4. Восстановленный сигнал при N = 256

Fig. 4. Reconstructed signal at N = 256

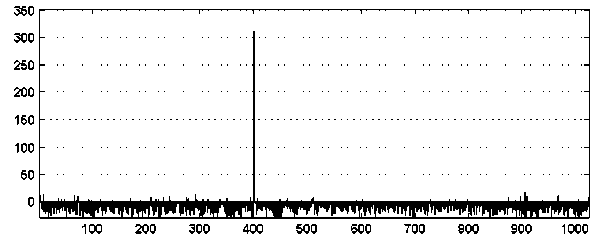
Рис. 5. Восстановленный сигнал при N = 1024

Fig. 5. Reconstructed signal at N = 1024

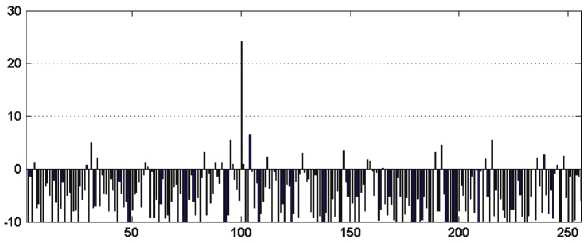
Рис. 6. Восстановленный сигнал при длине случайного фрагмента 70 %

Fig. 6. Reconstructed signal with a random fragment length of 70 %

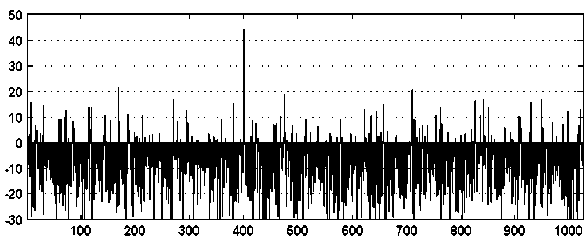
Рис. 7. Сигнал на выходе декодера при N = 1024. Длина случайного фрагмента 80 %

Fig. 7. Signal at the decoder output at N = 1024. Random fragment length 80 %

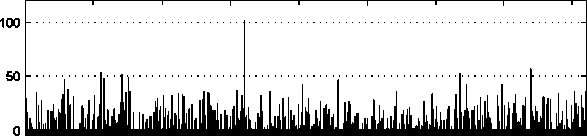
Если шум в канале искажает 90 % сигнала, необходимо увеличить длину кодовой комбинации до N = 4096, чтобы получить отношение сигнал/шум на выходе декодера 5 дБ (рис. 8).

-50

600      1000     1500     2000     2500     3000     3600     4000

Рис. 8. Потери в канале 90 %. Восстановленный сигнал при N = 4096

Fig. 8. Channel losses 90 %. Reconstructed signal at N = 4096

Исследование зависимости корректирующей способности голографического кода от расстояния между объектом и голограммой L , шага голограммы d и длины волны λ показало, что наилучшие результаты достигаются при значениях L = nd и λ = d .

Рассмотрим возможности кода по исправлению ошибок.

Корректирующие способности помехоустойчивого кода, имеющего n = 2 ^k символов в кодовой комбинации, из которых k символов информационные, оцениваются максимальным количеством ошибок t , которые он может исправить при заданной степени избыточности, например, для кода Рида – Маллера (РМ-код) t = 2 ^{k –2} – 1 [20], что соответствует исправлению ошибок любого вида, составляющих до 25 % длины кодового слова.

Одним из самых эффективных из известных кодов для исправления ошибок является код Рида – Соломона (РС-код), широко применяемый в помехоустойчивом кодировании, в системах восстановления данных с компакт-дисков, при создании архивов с возможностью восстановления информации в случае повреждений [21]. Предел корректирующей способности ( n , k ) РС-кода определен границей Синглтона [22], в соответствии с которой для исправления t ошибок код должен иметь не менее n – k = 2 t проверочных символов, т. е. два проверочных символа на одну ошибку. При большой степени избыточности ( n >>  k ) число исправляемых ошибок t приближается к 50 % от длины кодового слова n . Например, РС-код (255,8) с коэффициентом избыточности 32 устраняет 123 ошибки, при этом в кодовом слове содержится 132 верных символа – ошибки занимают 48 % кодового слова. Особенностью РС-кода является то, что столь высокую исправляющую способность он демонстрирует только для пакетных ошибок [21]. В то же время для большинства цифровых каналов, описываемых моделью двоичного симметричного канала без памяти, характерны случайные ошибки. Если перейти от пакетных ошибок к равномерно распределенным по кодовому слову случайным ошибкам, максимальное число исправляемых РС-кодом ошибок составит t = n / 2 k – 1. Отсюда следует, что тот же вариант ( n , k ) РС-кода при n = 256, k = 8 исправляет 15 случайных ошибок, что составляет 6 % длины кодового слова.

Для оценки помехоустойчивости голографического кода проведено сравнение надежности передачи информации по каналу с аддитивным белым гауссовским шумом при использовании нескольких кодов. Рассмотрена зависимость вероятности ошибки декодирования от отношения сигнал / шум в канале для РС-кода, РМ-кода, мажоритарного кода и голографического кода. Для этого взяты рассмотренные выше предельные количества исправляемых ошибок для каждого кода и построена зависимость вероятности появления числа ошибок не больше предельного от отношения сигнал / шум. Во всех случаях число разрядов исходного слова – 8, длина кодового слова – 256 бит (скорость кодов R = 1/32). Результаты приведены на рис. 9.

Одним из наиболее надежных способов передачи информации в сильно зашумленных каналах является усреднение в пределах введенной избыточности с мажоритарным способом выбора решения. Однако оказалось, что голографический код является более помехоустойчивым и обеспечивает выигрыш на 2 дБ по сравнению с мажоритарным кодом, что позволяет получить вероятность ошибки декодирования 10–6 при отношении сигнал/шум S/N = –7 дБ. Возможности предложенного голографического кода определяются уровнем введенной избыточности: при коэффициенте избыточности q = 32 происходит безошибочное декодирование сигнала при замене 70 % сигнала случайной последовательностью, в то время как используемый в ГЛОНАСС код Хэмминга исправляет одну ошибку в 85-разрядном слове.

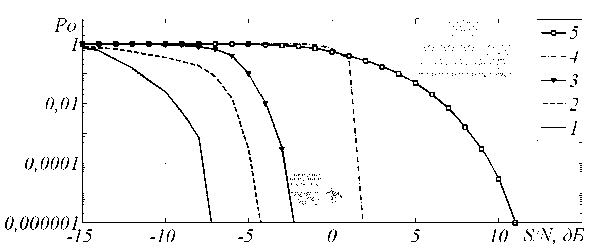
Рис. 9. Зависимость вероятности ошибки декодирования P_О от отношения сигнал / шум при скорости кода R = 1/32:

1 – голографический код; 2 – мажоритарный код; 3 – РМ-код; 4 – РС-код; 5 – без кодирования

Fig. 9. Dependence of the probability of decoding error P_O on the signal-to-noise ratio at code rate R = 1/32: 1 – holographic code; 2 – majority code; 3 – RM code; 4 – RS code; 5 – without coding

Все виды помехоустойчивого кодирования, в том числе и голографический код, требуют введения избыточности. Приведенные на рис. 9 результаты сравнения кодов получены при одинаковой скорости кода R = 1/32, т. е. при одинаковой 32-кратной избыточности. Другие коды работают и при небольшой избыточности, но с гораздо меньшей эффективностью. При использовании каналов связи с низким отношением сигнал / шум голографический код может повысить помехоустойчивость на порядок, но для этого необходимо введение как минимум 10-кратной избыточности. Это увеличивает объем передаваемой информации и при использовании того же канала связи увеличивает время передачи, а значит, и время определения координат. Поэтому возможности голографического кодирования в части длительности временного интервала определения координат необходимо соразмерять с поставленной задачей. Этот метод хорошо подходит для выполнения геодезических работ, но скорее всего, будет меньше востребован для измерения координат быстро движущихся объектов.

Заключение

Проведенные исследования показали, что введение голографического кодирования в канале спутниковой связи системы ГЛОНАСС даст возможность навигационной аппаратуре потребителей получать информацию с большего количества спутников за счет способности кода обеспечить возможность правильного декодирования сигнала при отношении сигнал /шум в спутниковом канале до –7 дБ, что существенно повысит точность позиционирования. Возникающая при этом проблема увеличения задержки выдачи координат может быть решена двумя методами: повышением скорости передачи информации в спутниковом канале либо организацией дополнительного канала с голографическим кодированием с тем, чтобы модифицированная навигационная аппаратура работала в двух режимах – быстром с текущей точностью и медленном, но более точном.

Благодарности. Работа выполнена при поддержке гранта Российского научного фонда, проект № 24-29-00080,

Acknowledgements. The study was supported by the grant of Russian Science Foundation № 24-29-00080,