Повышение управляемости криволинейного движения гусеничного трактора путем установки дифференциального механизма поворота и следящей системы

Введение . Известны механизмы поворота (МП) гусеничных машин, выполненные на базе гидрообъёмных передач (ГОП) [1–7]. В основном они применены в быстроходных машинах (танках, бронемашинах пехоты, тягачах) [8, 9]. Опыт применения аналогичных схем МП имеется и в тихоходных гусеничных машинах [10, 11], хотя он и не столь велик. Это связано с заметным удорожанием конструкции, необходимостью установки планетарных суммирующих передач и собственно ГОП. Целесообразность и преимущества перехода на бесступенчатый поворот промышленных тракторов требует обоснования. Отчасти оно изложено в данной статье.

Недостатки ГОП очевидны – низкий КПД, около 80 %. Преимущества же не очевидны: их надо разъяснять.

Во-первых, 80 % КПД соответствует всем радиусам поворота, от бесконечности до нуля, т. е. от движения, близкого к прямолинейному («подруливание» для компенсации увода), до поворота на месте вокруг центра тяжести. Роль МП большинства промышленных тракторов выполняют бортовые фрикционы (БФ) и тормоза. Критерием совершенства конструкции можно считать

Расчет и конструирование

величину потерь мощности при совершении полезной работы. Существует ошибочное мнение, что потери во фрикционном МП можно не учитывать, особенно когда речь заходит об их замене на гидрообъёмные. Как правило, фиксированный радиус поворота у трактора один (вокруг остановленной гусеницы), все остальные – промежуточные. Промежуточные радиусы (между фиксированными радиусами) достигаются пробуксовкой фрикционных устройств. Фрикцион, как и любой другой механизм, имеет свой КПД. Потери во фрикционе прямо пропорциональны проскальзыванию, т. е. разнице скоростей ведущих и ведомых дисков. Отпуская бортовой фрикцион, допускается частичная его пробуксовка. Мощность, проходящая через него, равна половине мощности ДВС. Каждый процент пробуксовки БФ соответствует 0,5 % мощности ДВС. В таблице приведена информация о потерях в БФ при повороте с радиусами (2...10) В, где В – поперечная база трактора, м.

Потери мощности N БФ в БФ вычисляют по формуле:

NБФ = P1A V , где P1 – сила тяги на отстающем борту, кН; ΔV – скорость буксования в БФ, приведенная к ведущему колесу, м/с.

Потери в БФ при повороте с промежуточными, нефиксированными радиусами

Радиус поворота	2В	3В	4В	5В	6В	7В	8В	9В	10В
Потери в БФ, %	50	33	25	20	17	14	12	11	10

Анализ таблицы подтверждает, во-первых, ошибочность представления об отсутствии потерь (или пренебрежимо малых потерях) в БФ как МП. Проценты потерь в БФ как раз и надо сравнивать с 20 % потерь в ГОП при любых радиусах.

Во-вторых, легкость управления ГОП с помощью джойстика или штурвала не достижима при управлении фрикционами. Фрикционы принципиально не могут обеспечить желаемое, да еще устойчивое, проскальзывание при постоянном положении рычага управления.

В-третьих, устойчивость движения по траектории промежуточного радиуса не гарантирована БФ, поскольку на проскальзывание фрикционных дисков влияет ряд факторов: управляющее воздействие водителя, сопротивление грунта, геометрическое состояние дисков, температура дисков, качество и температура масла и др. Компенсации внешних факторов нет, вся ответственность – на водителе, его квалификации. Фрикционы часто выходят из строя. Требуется время на их замену. Это простои трактора.

ГОП по всем перечисленным выше параметрам выигрывает.

Математическая модель . Структурная схема трансмиссии исследуемой гусеничной машины (ГМ) приведена на рис. 1. Особенностью исследуемой машины является порядок соединения основных звеньев СПР с турбиной ГТ (водило СПР), мотором ГОП (солнце СПР) и ведущим колесом (эпицикл СПР). Ни в одной из ана-

----гоп----- две ГТ ВК Ц СПР И кп Н спр Н вк Рис. 1. Кинематическая схема ГМ: ДВС – двигатель внутреннего сгорания, ГОП – гидрообъёмная передача механизма поворота, ГТ – гидротрансформатор, СПР – суммирующие планетарные ряды, КП – коробка передач, ВК – ведущие колеса

логичных машин, упомянутых выше, такого порядка соединения нет. Эта особенность нашла отражение в (5) и (6) уравнениях математической модели. Расчетная схема плоскопараллельного движения ГМ в неподвижных декартовых координатах приведена на рис. 2. Согласно расчетной схеме положение машины на плоскости задано двумя линейными координатами центра тяжести x C , y C и курсовым углом φ, показывающим отклонение продольной оси машины от оси координат Y .

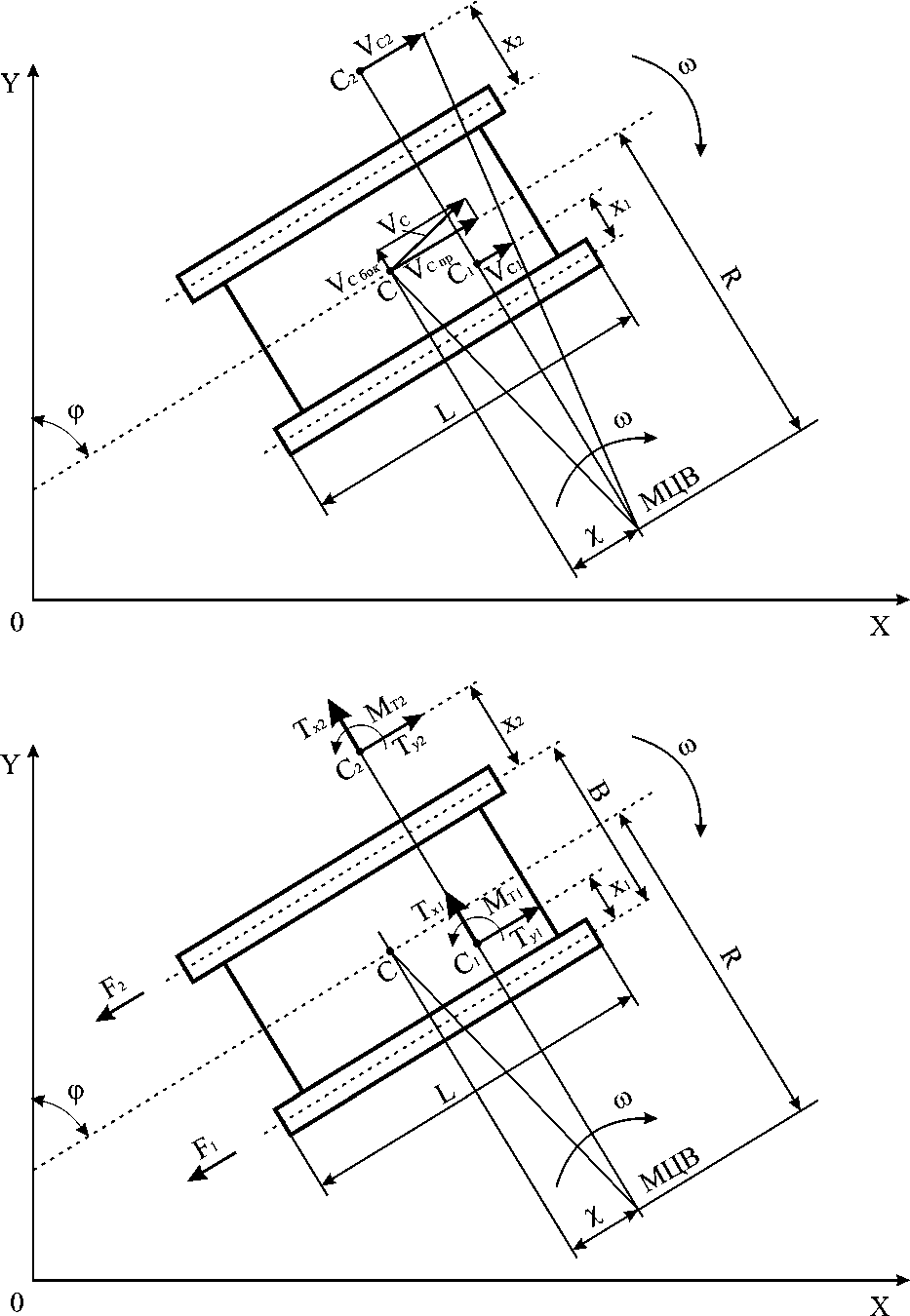
Рис. 2. Расчетная схема: X, Y – декартовы координаты, φ – курсовой угол, МЦВ – мгновенный центр вращения, F 1 , F 2 – силы сопротивления на отстающем и забегающем борту, V c – линейная скорость центра тяжести, χ – продольное смещение полюса поворота, L – продольная база машины, В – поперечная база машины, x 1 – поперечное смещение полюса поворота отстающей гусеницы, x 2 – поперечное смещение полюса поворота забегающей гусеницы, V С бок – составляющая V С , направленная перпендикулярно оси корпуса машины, V С пр – составляющая V С , направленная вдоль оси корпуса машины, T x1 , T y1 – составляющие результирующей силы трения отстающей гусеницы о грунт, T x2 , T y2 – составляющие результирующей силы трения забегающей гусеницы о грунт, М т1 , М т2 – результирующие моменты трения отстающей и забегающей гусениц относительно полюсов поворота С 1 и С 2 соответственно, ω = dφ / dt – угловая скорость поворота корпуса, V С1 , V С2 – скорости полюсов поворота отстающей и забегающей гусениц соответственно

Математическая модель, положенная в основу исследований маневренности ГМ, включает 8 дифференциальных уравнений первого и второго порядка. Три уравнения описывают плоскопараллельное движение корпуса машины, три - вращение коленчатого вала двигателя внутреннего сгорания, турбины гидротрансформатора (ГТ) и выходного вала мотора ГОП, два последних уравнения описывают динамику изменения давления в магистралях ГОП [12-14]:

Расчет и конструирование

d ² X_c dT ² d ² Y_c dT ² d ² ф dT ²

^L = [ ( T x 2 ⁺ T x 1 ^- F 1 ^- F 2 ) sin Ф ⁺ ( T y 2 ⁺ T y 1 ) cos ф] G ; = [ ( T x 2 ⁺ T x 1 ^{- F} 1 ^- F 2 ) cos ^ф- ( T y 2 ⁺ T y 1 ) sin ^ф] G ^;

= ( T x 2 - T x 1 + F

-

Т 1

⁺ M T 2 ) _T ;

_ J c

dT -[ Mд h - M н - М г. i 2 ] J - ;

d гот dT dTOM dT

M т

M гм

dP гоп1 dT

dP гоп2 dT

( T x 2 + T x 1 ) R вк ( к + 1 ) i бп i к к

( T x 2 - T x 1 ) R вк i бп i 5 к

= ( Q .1 - Q m1

J 2 ;

1 J 3 ;

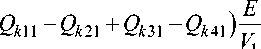
E

= ^{( Q} м2 ^{- Q} н2 ^- Q k 12 ^- Q k 22 ⁺ Q k 32 ^- Q k 42 )T^ ,

V ₂

здесь Т – текущее время, с; X_с , Y_с – координаты центра тяжести БГМ, м; φ – курсовой угол, рад; го . , го т , го м - частоты вращения насосного колеса гидротрансформатора (ГТ), турбинного колеса ГТ и мотора ГОП, рад/с; G – вес машины, Н; g – ускорение силы тяжести, м/с²; J С , J 1 , J 2 , J 3 – момент инерции корпуса относительно вертикальной оси, проходящей через центр тяжести, моменты инерции двигателя, турбины ГТ и мотора ГОП, кгм²; М с , М д , М н , М т , М гн , М гм – моменты сопротивления, двигателя, насоса ГТ, турбины ГТ, насоса ГОП, мотора ГОП соответственно, Нм; R вк – радиус ведущего колеса, м; i к , i 1 , i 2 , i 5 , i бп – передаточные числа в трансмиссии; к – параметр суммирующего планетарного ряда; P ГОП1 , P ГОП2 – давления рабочей жидкости в силовых магистралях, МПа; Е ( P , B , n ) – модуль упругости жидкости, зависящий от давления Р , газосодержания В и показателя политропы n ; Q i – расходы насоса и мотора ГОП, клапанов, дросселей и др., м³/с; V i – объемы соответствующих магистралей, м³.

Уравнения связи. Задающим воздействием в модели является поворот штурвала (джойстика), смоделированный во времени. Поворот штурвала приводит к изменению моментов на насосе и моторе ГОП по следующим уравнениям:

M гн = ^ гоп1 q н u н ^- ^ гоп2 q н u н ^-А М гн ;                                                        ⁽⁹⁾

M гм = ^ гоп1 q м u м ^{- Р}гоп 2 q м u м ^{- А М} гм ,                                                        ⁽¹⁰⁾

где M гопн и M гопм – моменты на насосе и моторе ГОП, P гоп1 и P гоп2 – давления в магистралях нагнетания и всасывания ГОП, q н и q м – объёмные постоянные насоса и мотора, u н и u м – параметр регулирования насоса и мотора. В исследуемом механизме поворота ГМ регулируется насос, связанный через систему управления наклонной шайбой ГОП со штурвалом. Параметр регулирования мотора остается постоянным и равным единице. Потери в гидрообъёмном приводе играют важную роль в достоверности описания работы механизма поворота. В модели использована методика учета потерь, приведенная в работе [1]. Расходы насоса и мотора формируются уравнениями:

^Q н1 = q н u н ^ГО гопн ^{-А Q} гн ;                                                                        ⁽¹¹⁾

Q м1 = q м u м ^го гопм ^{- А} Q гм .                                                                        ⁽¹²⁾

Далее наряду с расходом предохранительного клапана и клапана подпитки они входят в правую часть дифференциального уравнения (7) и формируют давление в магистрали нагнетания P гоп1 . Аналогично формируется правая часть уравнения (8) для магистрали всасывания.

Моменты насоса и мотора, определенные уравнениями (9) и (10), входят в правые части дифференциальных уравнений (4) и (6). Частота вращения двигателя, насоса гидротрансформа- тора и насоса ГОП связаны постоянными передаточными числами и определяют момент двигателя по его статической характеристике.

Фактические скорости движения, сначала заданные начальными условиями, а затем формирующиеся системой дифференциальных уравнений, сравниваясь со скоростями вращения гусениц, определяют буксования, которые, в свою очередь, формируют тяговые усилия на забегающем Р 2 и отстающем Р 1 борту.

Моменты на рабочих колесах ГТ определены по формулам:

М н =γλ D а ⁵ ω ² н ,                                                                        (13)

М = М к ,                                                                 (14)

тнг где Мн и Мт – моменты на насосе и турбине ГТ, γλ – коэффициент момента насоса ГТ, Dа – активный диаметр ГТ, кг – коэффициент трансформации ГТ.

Таким образом, система уравнений (1)–(8) описывает криволинейное управляемое движение ГМ и ее элементов: ДВС, насоса и турбины ГТ, насоса и мотора гидрообъёмной передачи механизма поворота.

Результаты моделирования. В процессе имитационного моделирования исследованы параметры криволинейного движения трактора с дифференциальным механизмом поворота. Вход в поворот трактора инициирован полным поворотом штурвала за 2 с. Так как особый интерес представляет работа ГОП, на рис. 3 приведен график относительного (относительно 40 МПа) давления в магистралях нагнетания и всасывания – для третьей передачи.

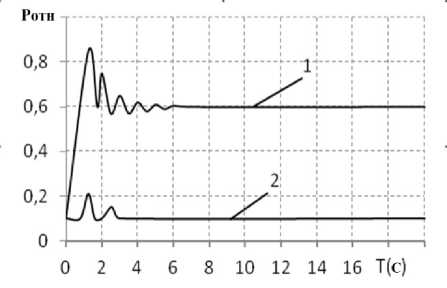
Рис. 3. Относительное давление в магистрали нагнетания (1) и всасывания (2) для третьей передачи, коэффициент сопротивления φ = 0,1

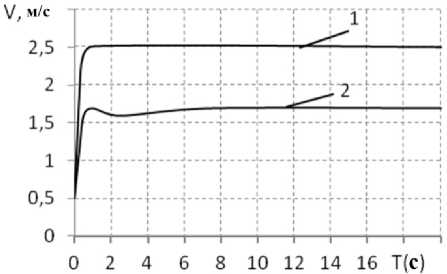
Рис. 4. Скорость трактора при работе на грунте с коэффициентами сопротивления φ = 0,1 (1), φ = 0,3 (2)

Поскольку грунт задан один и тот же, то и установившиеся давления одинаковы, порядка 0,6 от 40 МПа, т. е. 24 МПа. Важно отметить, что при входе в поворот давление превышает установившееся в 1,5 раза, и это обстоятельство надо иметь в виду, из статических расчетов эту цифру не получить, а при испытаниях реальной машины потенциальная неспособность войти в поворот может быть связана именно с этим.

Далее исследовано аналогичное движение, но на грунте с большим сопротивлением (в 3 раза больше). На рис. 4 изображена скорость трактора. Интересный, но очевидный результат: чем больше сопротивление, тем больше проседает турбина ГТ и скорость ГМ меньше. Неочевидность в другом – вход в поворот сопровождается скачком давления ГОП, причем в случае меньшего сопротивления, но большей скорости – скачок гораздо больше, на 15 % (см. рис. 5).

При развороте на месте примерно та же картина: при большом сопротивлении – скачок давления (см. рис. 6). Меньшему сопротивлению соответствует большее давление в переходном процессе, даже выходит на клапан. Дело в том, что сила тяги на забегающем борту достигает предела при φ = 0,3 и не дает отстающему борту развить необходимую отрицательную тягу. А это отражается на развиваемой угловой скорости разворота на месте (см. рис. 7).

Разворот на месте реализуется силами тяг по бортам, а точнее разницей между силой тяги по сцеплению и силой сопротивления грунта на каждом борту. Меньшее сопротивление оставляет достаточный запас по сцеплению для поворачивающего момента, загрузки ГОП и развития необ-

Расчет и конструирование

ходимой скорости поворота (разворота на месте). Рис. 7а иллюстрирует невозможность достижения теоретической угловой скорости в 0,5 рад/с при сопротивлении φ = 0,3.

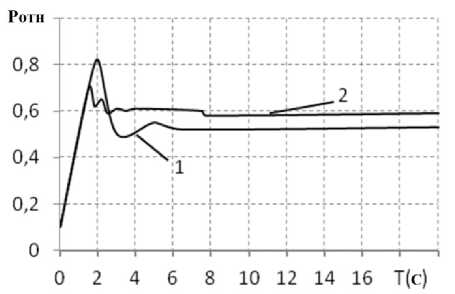
Рис. 5. Давление в магистралях ГОП при повороте на третьей передаче и коэффициентах сопротивления грунта: 1 – φ = 0,1; 2 – φ = 0,3

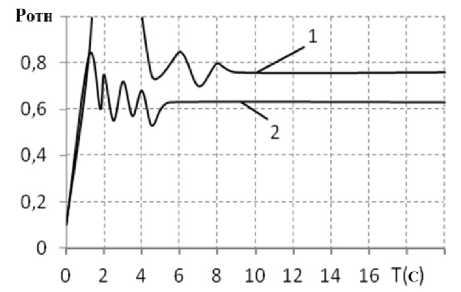
Рис. 6. Давление в магистралях ГОП при развороте на месте: сопротивления грунта: 1 – µ = 0,7, φ = 0,1;

2 – µ = 0,7, φ = 0,3

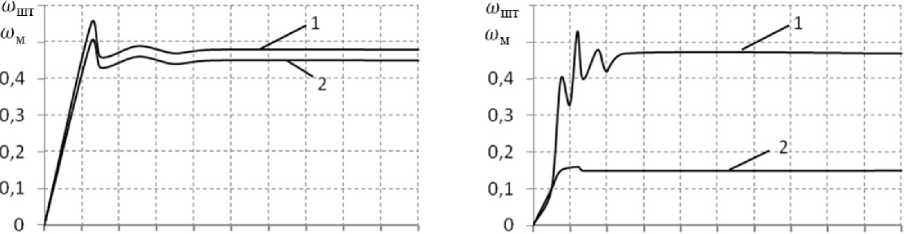
О 2 4 б 8 10 12 14 16 Т(с)              0 2 4 6 8 10 12 14 16 Т(с)

а)                                                                    б)

Рис. 7. Угловая скорость разворота на месте: а – µ = 0,7, φ = 0,1; б – µ = 0,7,φ = 0,3: 1 – теоретическая, по ведущим колесам; 2 – реальная, на грунте

При сопротивлении φ = 0,1 перегрузка по давлению (рис. 8) возникает по причине достаточной разницы коэффициента сцепления и сопротивления, что порождает большое угловое ускорения корпуса ГМ. В результате угловая скорость разворота на месте достигает расчетных по статике величин – 0,5 рад/с. Почему же не 0,63 рад/с? Из-за буксования гусениц порядка 5 % и потерь в ГОП порядка 20 %. И то, и другое не учитывается в статическом расчете.

Моделирование следящей системы стабилизации траектории движения ГМ [15, 17–20]. Известны классические различия в схемах механизмов поворота американских и немецких танков и БМП: у «Абрамса» насос ГОП приводится от турбины ГТ, а у «Леопарда-2» – непосредственно от ДВС. Считается, что в немецкой схеме больший КПД, так как мощность, затрачиваемая на поворот, не проходит через ГТ с его 70%-ным КПД. Однако есть и существенный недостаток – при увеличении сопротивления грунта турбина ГТ самопроизвольно «просаживается», а ДВС сохраняет свою скорость вращения, что совместно приводит к уменьшению радиуса траектории при неизменном положении штурвала. В связи с этим считается, что «Абрамс» управляется в повороте лучше, чем «Леопард-2».

В исследуемой схеме недостаток привода насоса ГОП от ДВС налицо (см. рис. 8). В момент времени t = 5 с коэффициент сопротивления грунта увеличен с 0,2 до 0,6, что приводит к самопроизвольному уменьшению радиуса с 13,5 до 10 м. Это связано с уменьшением передаточного отношения ГТ с 0,88 до 0,65.

Авторами предложено формировать управляющее воздействие на насос ГОП с учетом дополнительной информации о скорости вращения турбины ГТ, корректируя таким образом подачу насоса ГОП независимо от положения штурвала.

При бульдозировании единичный скачок возмущения возможен при наезде на препятствие в виде камня в грунте. Чаще же сопротивление возрастает постепенно по мере набора грунта в призме. Оценено влияние процесса набора грунта на трактор, не оснащенный следящей системой и оснащенный ей. Сравнительные результаты приведены на рис. 9: графики показывают, что при бульдозировании в повороте радиус траектории у трактора, не оснащенного следящей системой, самопроизвольно уменьшается с 6 до 4,5 м, т. е. на 25 %. Оснащение трактора следящей системой позволит стабилизировать криволинейную траекторию, сделать ее независимой от изменяющейся внешней нагрузки.

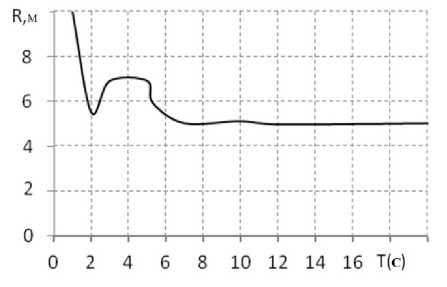
Рис. 8. Радиус траектории движения ГМ при увеличении сопротивления с φ= 0,1 до φ= 0,3 в момент времени 5 с

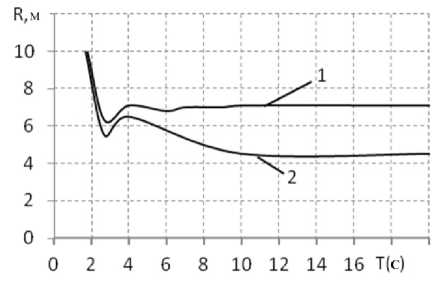
Рис. 9. Радиус траектории трактора при постепенном наборе грунта: 1 – со следящей системой; 2 – без следящей системы

Одно из важных преимуществ ГОП в механизме поворота – возможность её бесступенчатого регулирования. В работе [15] впервые предложено использовать обратную связь при регулировании положения наклонной шайбы (НШ) насоса ГОП по отклонению кривизны траектории k 0 , задаваемой штурвалом, от текущей кривизны траектории k гм , реализуемой ГМ на местности. Регулирование положения НШ насоса именно по Δ k = k 0 – k гм позволяет обеспечить движение ГМ по замкнутой траектории независимо от влияния внешних возмущений f со стороны грунта, поскольку стабилизация к гм = R - 1 , где R - радиус разворота ГМ, это, по сути, обеспечение R = const при f = var. Текущая кривизна траектории движения центра масс ГМ k гм в системе вычисляется следующим образом:

к = ^м гм ,

Vм где ωм – угловая скорость поворота машины, измеряемая вибрационным датчиком угловой скорости – микромеханическим гироскопом, Vм – продольная скорость центра тяжести машины, оцениваемая датчиком частоты вращения выходного вала коробки передач.

Структурная схема системы стабилизации кривизны траектории ГМ при изменении сопротивления грунта приведена на рис. 10.

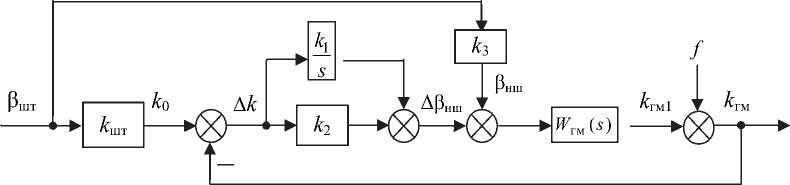
Рис. 10. Структурная схема системы с дополнительным регулированием наклонной шайбы ГОП

Наклонная шайба (НШ) насоса ГОП соединена со штурвалом дифференциальной связью с моделью k 3 , позволяющей поворачивать шайбу на угол β нш . Кроме этого, на рис. 10 обозначены: β шт – угол поворота штурвала, соответствующий заданной угловой скорости поворота ГМ; k шт – коэффициент передачи преобразователя β шт в заданную кривизну траектории k 0 ; W гм (s) – передаточная функция ГМ; f – возмущение (изменение k гм , вызванное влиянием изменяющейся нагруз-

Расчет и конструирование

ки со стороны грунта); k 1 , k 2 – настроечные параметры регулятора; ∆ β нш – дополнительный угол поворота НШ, формируемый системой независимо от водителя по величине ∆ k .

Количественная оценка управляемости. В настоящее время теория криволинейного движения гусеничных машин трактует управляемость к а к качество [16], без количественной оценки. Введение системы дополнительного регулирования н асоса ГОП по отклонению кривизны траектории движения машины логично потребовало количественной оценки управляемости:

0 = k⁰

k^ - 100%.

Рис. 11. Зависимость от времени радиуса поворота при входе в поворот и смене грунта

Имитационное моделирование движения ГМ в некоторых стандартных условиях показало следующие результаты.

• 1.    Движе н ие по кругу. Радиус тр а ектории становится в полное соотв е тствие штурвалу, без дополнительного регулирования радиус отличался от задаваемого ш турвалом в 1,5 раза (из-за буксования).

• 2.    Изменение грунта. Увеличение соп р отивления в 2 раза на пятой секунде движения (рис. 11) приводит к самопроизвольному уменьшению р адиуса поворота на 0,8 м (график 1), а при дополнительном регулировании наклонной шайбы ГОП радиус траектории с о храняется неизменным на любых грунтах (график 2). Кроме того,

при отсутствии дополнительного регулирования н а клонной шайбы ГОП буксование гусениц приводит к увеличению установившегося радиуса поворота с 5,4 до 7,4 м.

Выводы

• 1.    Развита математическая модель движения гусеничной машины введением новой схемы

• 2.    Установлено, что при входе в поворот на в ы сшей передаче давление в ГОП м еханизма поворота в полтора раза превышает установившееся значение.

• 3.    При входе в поворот на тяжелых грунтах не хватает сцепления с г р унтом для осуществления маневра.

• 4.    При начале разворота на месте на грунте с коэффициентом сопрот и вления повороту более 0,7 давление в магистрали ГОП достигает 40 МП а .

• 5.    Предложен алгоритм дополнительного управления подачей насоса ГОП, позволяющий стабилизировать кривизну траектории при изменении сопротивления движению ГМ с о стороны грунта.

• 6.    Показано, что при реализации автоматической системы дополнительного регулирования подачи ГОП на основе данных с устройств GPS-навигации ошибка управления криволинейным движением гусеничного трактора сводится к нулю.

соединения потоков мощности в механизме передач и поворота гусеничного трактора и модели следящей системы поддержания стабильного радиуса при неизменном положении штурвала

Работа выполнялась при финансовой поддержке Министерства образования и науки Российской Федерации в рамках комплексного проекта по созданию высокотехнологичного производства «Разработка бесступенчатого дифференциального механизма поворота со следящей системой управления для внедорожных и дорожно-строительных машин нового поколения» по соглашению № 074-11-2018-006 от 31.05.2018 г. между Министерством образования и науки Российской Федерации и Обществом с ограниченной ответственностью Производственная компания «Ходовые системы» в кооперации с Головным исполнителем НИОКТР – Федеральным государственным автономным образовательным учреждением высшего образования «ЮжноУральский государственный университет (национальный исследовательский университет)».