Практическое применение непрерывной многокритериальной задачи

В настоящее время продолжаются исследования многокритериальных оптимизационных задач. Изучение литературы в этой области показало, что новых применений на практике многокритериальных задач за последнее время найдено немного. В качестве примера исследовательской работы в этой области приведём задачу об изготовлении колбасной смеси [1] и задачу равновесного программирования, которая решалась в [2]. В связи с изложенным далее будет сформулирована двухкритериальная задача о рационе. Решение которой на практике позволит получить экономическую выгоду предприятию, занимающемуся изготовлением смесей. Отметим, что двухкритериальная задача, формулируемая в статье, относится к классу непрерывных многокритериальных задач.

В последующем разделе описываются формальная и содержательная постановки исследуемой задачи. А также выполняется анализ результатов её решения.

Анализ двухкритериальной задачи о рационе

Приведём формальную постановку задачи о рационе:

C = с^ • x ^ + С 2 • Х 2 + ... + c^_n • x_n ^ min

V = x j + X 2 + ... + xn ^ max

V >  b

C ^ P

A = a^ j • X j + a^ 2 • x^ + ... + a^_n • xn >  b

A 2 = a 21 • x i + a 22 • x 2 + ... + a 2 n • xn >  b 2

Am = am i • ^x 1 ⁺ am 2 ' ^x 2 ⁺ ... ⁺ amn 'xn >  bm xj >  0, j = 1,2,..., n

Далее рассмотрим содержательную постановку задачи о рационе. Задан ассортимент различных продуктов в количестве n . Каждый продукт содержит определённое количество питательных веществ m видов. Необходимо определить оптимальный рацион, максимизируя его объём. Рацион должен иметь минимальную стоимость. Причём задано ограничение на дневной объём рациона - b и известна сумма, имеющаяся у предприятия на изготовление смеси - p .

Обозначения в (1) имеют следующий смысл:

aij

- содержание i -ого питательного вещества в j -ом продукте;

b - количество i -ого необходимого питательного вещества;

cj

дукта; x_j

– стоимость единицы j -ого про-

– количество j -ого продукта, вхо- дящего в рацион.

Рассмотрим индивидуальную задачу (2), соответствующую постановке задачи (1). В качестве прототипа задачи (2) использовалась однокритериальная задача об оптимальном составлении рациона, представленная в работе [3].

0,3 • Х | + 0,9 • Х 2 ^ min

• Х | + X 2 ^ max

X | + X 2 > 800                 (2)

0,3 • x _T + 0,9 • x ₂<  3000

0,21 X | - 0,3 • X 2 <  0

0,03 • x _T - 0,01 - x ₂ >  0

xj >  0, j = 1,2

Построим однокритериальную задачу (3). В агрегированном критерии этой задачи критерии задачи (2) имеют одинаковые приоритеты, их веса 0,5:

• - 0,5 • ( 0,3 • X j + 0,9 • X 2 ) + 0,5 • ( x ^ + X 2 ( ^ max

X j + X 2 >  800                               (3)

0,3 • x j + 0,9 • x ₂<  3000 0,21 . x j - 0,3 ' x ₂<  0 0,03 " x ₁ - 0,01 " x ₂ >  0 xj >  0, j = 1,2

Преобразованный критерий задачи (3) имеет вид: 0,35 • x ^ + 0,05 • x^ ^ max . Задача (3) решалась в среде программы lp_solve. В результате вычислений получили x =3225,80; x =2258,06; V

=5483,86; C =2999,994. На рисунке 1 представлен скриншот результатов работы программы при решении задачи (3):

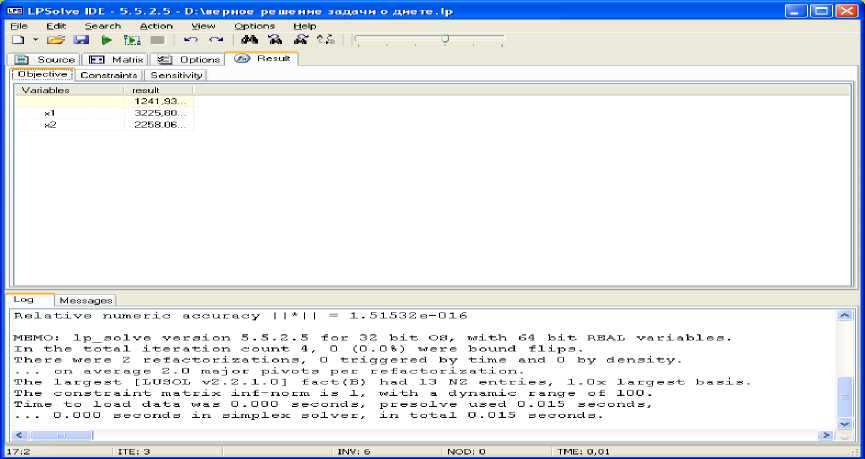
Рис. 1. Результаты работы программы при решении задачи

Преимуществом задачи (2) в отличие от прототипа является дополнительное ограничение сверху на стоимость смеси и одновременная максимизация объёма смеси с минимизацией стоимости. Сравним задачу (2) с онокритериальной задачей (4), в которой в качестве единственного критерия рассматривается стоимость смеси:

0,3 • x ^ + 0,9 • x^ ^ min x ^ + x^ >  800 0,3 • x T + 0,9 • x 2<  3000          (4) 0,21 x ^ - 0,3 • x^ <  0 0,03 • x ^ - 0,01 • x^ >  0 xj >  0, j = 1,2

Задача (4) решалась в среде программы lp_solve. В результате вычислений получили x =470,58; x =329,41; V =799,99;

C =437,64. На рисунке 2 представлен скриншот результатов работы программы при решении задачи (4):

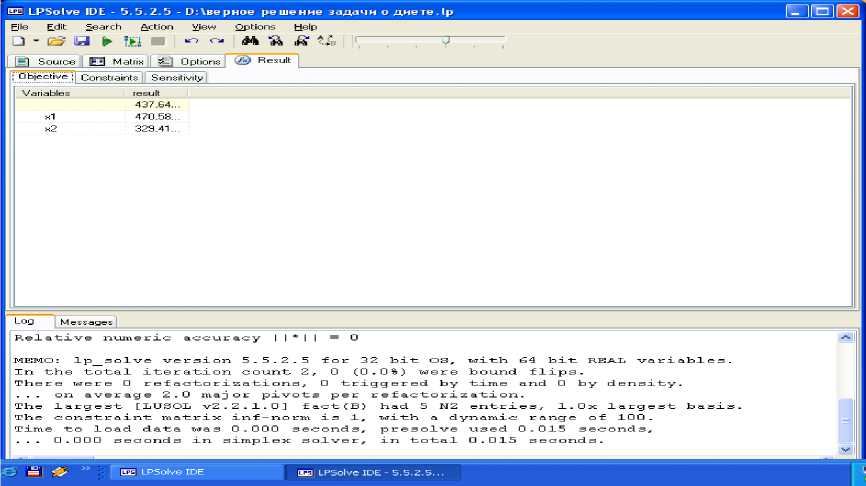
Рис. 2. Результаты работы программы при решении задачи

В последующем разделе подводятся итоги проведённого в статье анализа двухкритериальной задачи о рационе, принадлежащей классу непрерывных многокритериальных задач.

Заключение

Сформулированная в статье задача (1) имеет практическую ценность. А именно, результаты её решения позволяют предприятию рационально вкладывать капитал при расширении производства. Действительно, обладая фиксированной суммой финансовых средств p , предприятие может определить наибольший объём производства при этих затратах. Заметим, что оптимальное решение задачи (1) на примере её индивидуальной постановки (2) эквивалентно оптимальному решению классической задачи (4). А именно, оценим отношение оптимальной стоимости

C задачи (2) к соответствующей характеристике C кл классической задачи (4). Получим:

C2   2999,994

Cкл 437,64 ~ 6,85

Оценим отношение оптимальных объёмов рациона задачи (2) и задачи (4):

V ²

_V кл

5483,86

799,99

« 6,85

То есть, применение двухкритериальной задачи о рационе является практически выгодным, а её решение не хуже (эквивалентное) решения однокритериальной задачи о рационе. А в задаче (1) не только минимизируется стоимость смеси, но и максимизируется её объём, в отличие от прототипа, что на практике позволяет более рационально вкладывать финансовые ресурсы предприятия и максимизировать объём производства.