Predator and Prey Modified Biogeography Based Optimization Approach (PMBBO) in Tuning a PID Controller for Nonlinear Systems
Автор: Mohammed Salem, Mohamed. F. Khelfi
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 11 vol.6, 2014 года.
Бесплатный доступ
In this paper an enhanced approach based on a modified biogeography optimization with predator and prey behavior (PMBBO) is presented. The approach uses several predators with new proposed prey’s movement formula. The potential of using a modified predator and prey model is to increase the diversification along the optimization process so to avoid local optima and reach the optimal solution quickly. The proposed approach is used in tuning the gains of PID controller for nonlinear systems (Mass spring damper and an inverted pendulum) and has given remarkable results when compared to genetic algorithm and classical BBO.
Biogeography Based Optimization, Predator And Prey, Modified Migration, PID Control, Nonlinear System, Genetic Algorithms, Inverted Pendulum
Короткий адрес: https://sciup.org/15010621
IDR: 15010621
Текст научной статьи Predator and Prey Modified Biogeography Based Optimization Approach (PMBBO) in Tuning a PID Controller for Nonlinear Systems
Published Online October 2014 in MECS
Biogeography based optimization (BBO) is an evolutionary algorithm (EA) initially developed in [1]. It takes cue from the science of biogeography which studies the movement of species between islands moving from less habitable places to good ones. It operates by sharing information between candidate solutions (habitats).
Since its development, several researchers tried to enhance the BBO algorithm, so in [2], the performance of BBO is accelerated with the help of a modified mutation and clear duplicate operators while in [3], a blended migration operator was introduced. Authors of [4] proposed three variations of BBO called Total immigration BBO, Partial emigration BBO and Total emigration BBO using Markov models. In [5], modified migration and mutation operators are used in a biogeography optimization of a PID controller.
PID controllers are easier and efficient solutions in engineering applications because they do not need prior knowledge of the process to be controlled. The PID control involves three gains to be determined Proportional, Integral and Derivative [8]. Adjusting the PID parameters is considered as an optimization problem which has been solved by evolutionary algorithms (EAs), including genetic algorithms [9, 10], ant colony optimization [11], particle swarm optimization [12, 13] and biogeography based optimization (BBO)[14].
In this paper we introduce a new approach: Predator and Prey based modified biogeography optimization (PMBBO) where a new modified migration operator is used to prevent best solutions from being deteriorating while the mutation is replaced by a predator and prey behavior in aim to ensure diversification and speed up the optimization process by avoiding to stay a lot of time in local optima. In difference with [6], we propose to consider a set of predator instead of one and to use a variable hunt rate and a new prey movement formula is also introduced.
The remainder of this paper is organized as follows: The PID control structure is defined in section 2 while Section 3 is dedicated to the original biogeography based optimization (BBO).
Section 4 is dedicated to the proposed improvement approach is detailed where the new introduced operators are described and the chart of the proposed algorithm is given. The architecture of tuning PID controller with the PMBBO approach is presented in Section 5. The last section is divided to three subsections: In the first one, numerical simulations of the application of PMBBO in tuning PID controller for nonlinear systems (Mass spring damper and inverted pendulum) are presented. The second subsection presents a comparison of our approach with genetic algorithms and Biogeography based optimization. Finally, the third subsection is dedicated to a study of the influence of predators ’ number and hunt rate over the proposed approach.
-
II. PID C ONTROL
PID control consists of three components, Proportional, Integral and Derivative part (See Fig. 1) [8]. The controller aims to reduce the error between the plant output y(t) and the desired output yd(t) which is given in (1) [21]:
A = 1 1 1 - — s \ max
M = E
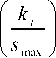
where smax is the maximum species number and ki is the rank of the habitat Hi after evaluation. The immigration and emigration curves are straight lines (See Fig.2). Simon's Classical migration process between habitats is defined by (4) [1]:
e (t ) = yd ( t ) - У (t )
H j (SIV c ) ^ H ( SIV C ) (4)
u(t), the output signal of the PID controller is given by (2) [8]:
• Step 3: Update species count probability of each habitat which is initially given by (5):
u (t ) = Kpe (t ) + Ke (t ) + K J e (t )dt . (2)
K p , K i and K d are positive constants to be adjusted to control the plant. This is done usually by trial/error in case of nonlinear systems [8].
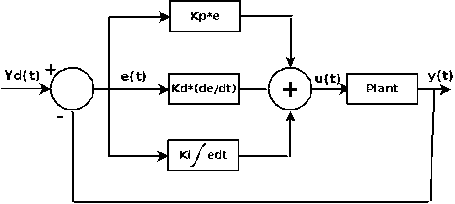
Fig. 1. PID control structure
P s = — (5)
max
In each iteration, the probability of an island is modified using (6):
P = P + P (6)
sss
where P is the variation of probability given by (7):
P s =
- ( A s + M s ) P s + M s + 1 P s + 1
- ( A s + M s ) P s + M s + 1 P s + 1
, s = 0
+ A s - 1 P s - 1 ,1 ^ s < s max
[- ( A s + M s ) P s + A s - 1 P s - 1 , s = s ma.
-
III. B IOGEOGRAPHY B ASED O PTIMIZATION
Biogeography based Optimization (BBO) is a stochastic optimization algorithm driven by the migration mechanisms of ecosystems. It is inspired by mathematical models of biogeography.
The BBO algorithm uses a vocabulary similar to that of biogeography where each habitat is similar to a solution of the problem; features of a solution are called suitability index variables (SIV). Each solution is evaluated and its quality is called the Habitat suitability index (HSI) which is analogous to the fitness in genetic algorithms.
The whole BBO algorithm could be explained as follows [14]:
-
• Step 1: The BBO starts by initializing the algorithm parameters: the SIV's number n siv and ranges,
maximum species number, termination criterion (iteration number or other performance criterion), maximum immigration and emigration rates E and I, mutation coefficient and define the appropriate HSI, then the start population islands are generated randomly[20].
-
• Step 2: Evaluate each island in the population, get its HSI value and map it to obtain the species count $s$. Immigration and emigration rates and are
calculated in this step by (3):
• Step 4: Apply the mutation operator which is introduced to add new features and increase population diversity [1]. The probability that the ith habitat is subject to mutation is given as follows[18, 19]:
mi = m max
1 -
Mutable islands are replaced by randomly generated solutions, where m max is a user-defined parameter called mutation coefficient and P s is the probability of existence of habitat i [1].
• Step 5: if the termination criterion is not reached then go to step 2.
-
IV. P REDATOR AND P REY MODIFIED BIOGEOGRAPHY OPTIMIZATION (PMBBO)
-
A. Modified migration operator
A modified migration operator was proposed in [5] basing on works of [3].
The new introduced operator does not only reconstruct existing islands but it can provide a new solution to the population witch increase diversity of the optimization problem. This operator shares information between habitats using (9):
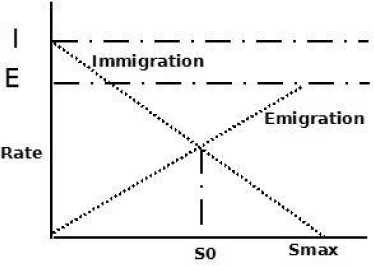
Fig. 2. Species Migration model
where p is the hunt rate whose value is given in (12), g is the current iteration and gmax is the maximum iteration number.
P =---
2* g
k
H j (SIV c ) ^ — j— H j (SIV c ) k, + k,
+ 1 -
kj kj + kt
H ( SIV )
We chose the value of ρ to be decreasing to the fact that, as iterations number increases, we need more to intensify the search than diversifying.
• For the next iteration, update other solutions values
(preys) H to make them run away from the predator ig in order to explore new parts of the search space. The new positions are calculated by (13):
H ig +1
=
[ H ig + p -d
In this paper, we propose that best islands shared information according to their quality against all other islands. Our migration operator is given in (10):
H i - p- d | g
d 0
d 0
i g * b
H j (SIV c ) <
s k max j H (SIV )
max
( kj )
+ j H ( sivc ) sc
\ max У
B. Predator and Prey model
Fig. 3. Predator and Prey model ([17])
• Assign the best island Hb to a predator by (11):
pred = H b + p (1 — ^) g max
where d is the distance between a prey and the predator.
C. Description of PMBBO algorithm
We propose to modify the BBO originally developed by [1] by introducing two major modification: First we replaced the original migration operator given by (4) by our novel operator in (10) to prevent best islands to be deteriorated, Second we propose to replace the mutation operator by Predator and prey model since it is a natural process like biogeography and it ensures diversification. Indeed, in nature species try to find habitable places and avoid predators. We propose also to use more then one predator, this is motivated by the fact that predators usually hunt in groups. let's g the number of predators in the group, Predators values are initialized to the g best islands, (11) will be:
ii gmax
New positions of preys are adjusted by (15) so closest solutions to the predator will explore new parts of the search space:
H i = H i + pp e -dm |( H i - H i ) i- ^ best (15)
g +1 g maxx mumg where d is the distance between island H and the closest predator:
gd dm =min d(Hi , Hpred )
j =1
H and H are the minimum and maximum imin possible ranges of the features of an island H, μ is a random number between -1 and 1. The new PMBBO approach is described by the Algorithm in Fig.4.
Algorithm 1: PMBBO
Initialize parameters.
Initialize predator number gd
Initialize start islands.
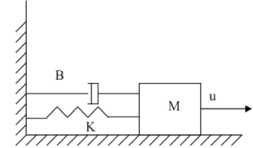
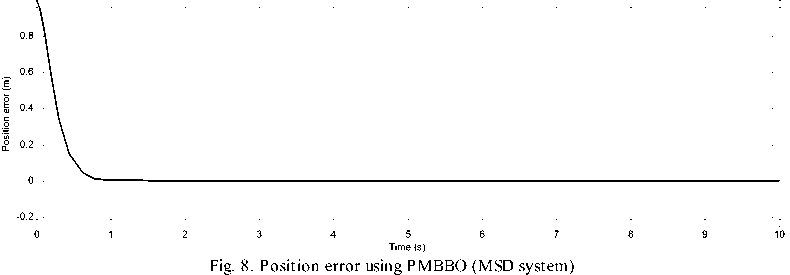
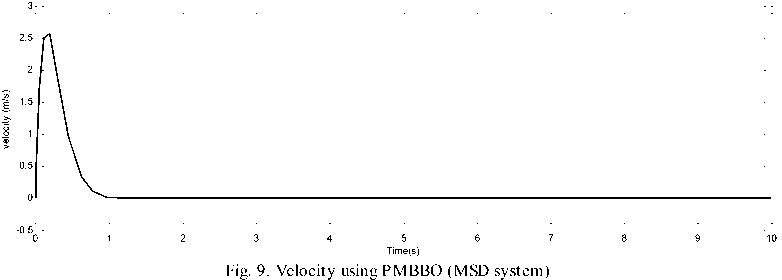
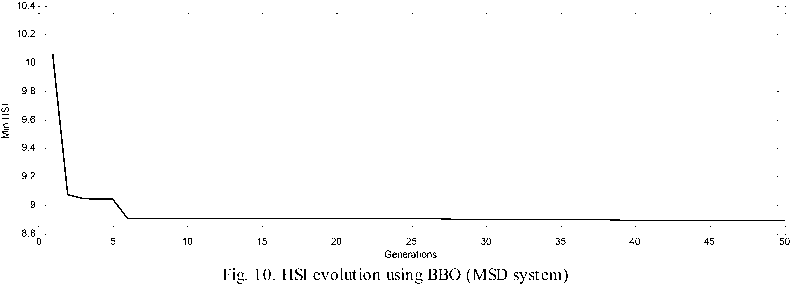
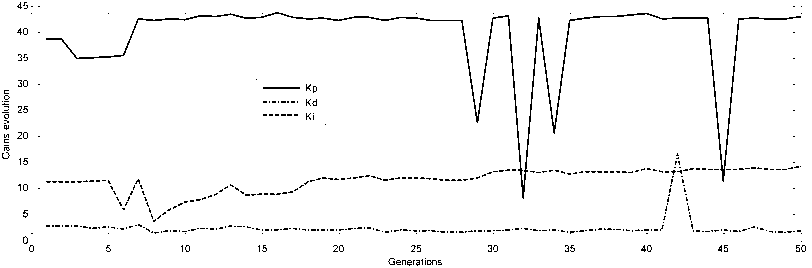
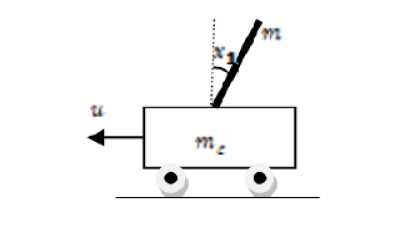
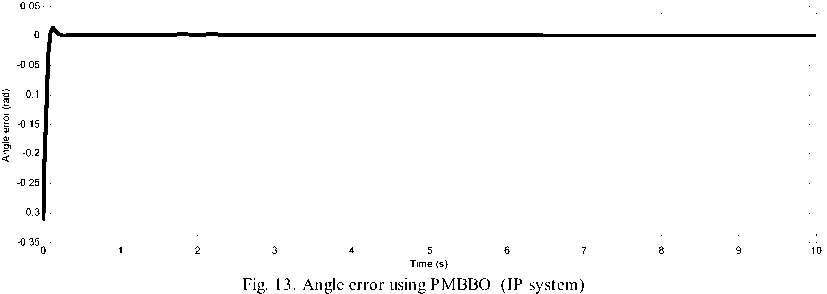
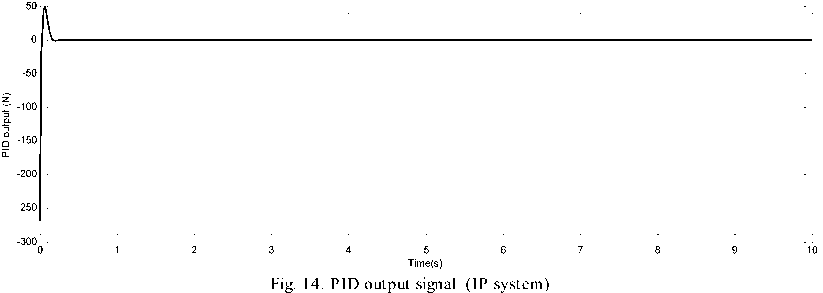
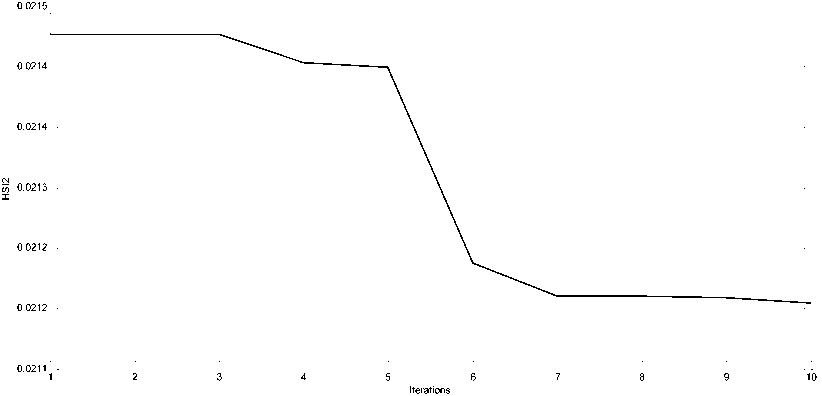
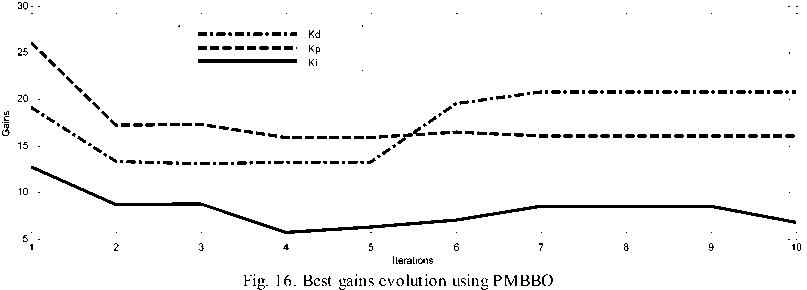
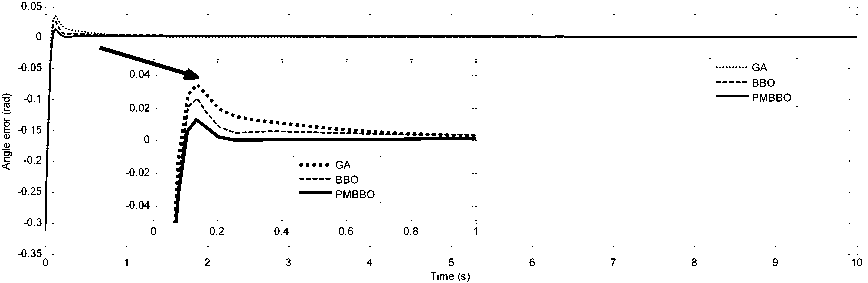
while g Calculate HSIi calculate λi and μi by (3). Apply the modified migration operator using (10). endfor Assign gd best islands to predators (Equations(14) for each island I do Calculate distance to all predators. Calculate dm by (16). Update island using (15). endfor endwhile Fig. 4. PMBBO algorithm V. TUNING PID CONTROLLER USING PMBBO Adjusting the PID parameters could be considered as an optimization problem where we try to find the optimal solution inside a predefined search space to fulfill a desired reference of a nonlinear system. In this context, the PMBBO algorithm could be used to find the optimal combination of the proportional, integral and derivative parts of the controller, so the variables of islands(SIV) in our problem are the three gains of the PID controller Kp, Ki, Kd. The gains must be in a user defined range regarding to the system physical limits (See (17)): Fig. 5. Tuning of PID controller using PMBBO VI. SIMULATION RESULTS To evaluate the proposed BBO improvement algorithm, it will be used to tune PID controller for two nonlinear systems A. Nonlinear Mass spring damper system A mass-spring-damper (MSD) nonlinear system with friction is considered (Fig.6) (19), where we want to move the mass accurately to the reference position (x=1 in our case) using a PID controller [8]. Fig. 6. Mass spring damper system The initial parameters for the PMBBO algorithm used in tuning the mass spring system, are in are in Table.1. Kp∈[Kp ,Kp ] minmax Ki ∈[Ki, minmax Kd ∈[Kd, minmax To evaluate the habitats, we use the objective functions HSI given by (18): Table 1. PMBBO parameters (Mass spring damper system) Population size 10 Generation number 50 Number of SIVs 3 E,I 1 Kp, Ki, Kd ranges [0,50], [0,50], [0,50] Predators number 3 HSI = ∫e2(t)dt (18a) HSI2=(1-ebeta)(Omax +es)+ebeta(Ts-Tr) (18b) where Ts and Tr are the settling and rise times respectively. Omax is the overshoot and es is the steady state error while beta is a weighting constant. The implementation of the PMBBO for tuning PID is shown in Fig.5. After running the PMBBO algorithm with the HSI in (18b), the optimal found gains are: Kp=42.9646 ; Ki= 14.2025; Kd= 1.8066. The desired and real positions are in Fig.7 while the position errors are in Fig. 8. Velocity of the mass is in Fig.9 Fig. 10 and Fig. 11 show the evolution of the HSI and best gains during the run of BBO respectively. Fig. 7. Real and desired Position using PMBBO (MSD system) Fig. 11. Best gains evolution using BBO (MSD system) The PMBBO algorithm has found the optimal gains in few generations (10 runs). The resulted gains give a good result in steady error and rising time (Fig. 8). B. Inverted pendulum system The second application of the PMBBO algorithm is to tune PID controller parameters to control a nonlinear inverted pendulum system (IP) (See Fig. 12) [15, 22]. The algorithm parameters are in Table.2 and HIS in (18a) was used. The obtained angle error of the pole is in Fig. 13, PID output signal in Fig.14. We see that the inverted pendulum angle converge to zero starting from (-π/10) with a small overshoot (0.0125rad) , settle and rise times are less then (0.1s). These good performances are obtained due to the optimization power of the PMBBO witch give us the best combination of Kp, Ki and Kd. Table.2. PMBBO parameters (Mass spring damper system) Number of Islands (Smax) 20 Generation number number (gmax) 10 Number of SIVs 3 E,I 1 Kp, Ki, Kd. range [0..100] Predators number 4 The evolution of the best HSI (18a) is in Fig.15 and the best gains of each iteration are in Fig.16. Fig. 12. Inverted Pendulum system Fig. 15. Min HSI of PMBBO (IP system) C. Comparing PMBBO approach to genetic algorithms The performances of the PMBBO had been compared to those of Genetic algorithm (GA) ,Biogeography based optimization (BBO), Modified migration based BBO (MBBO). The comparison was in the same conditions (iteration number, population size, initial population), the angle error of the inverted pendulum for GA, BBO and PMBBO are represented in Fig.17. for comparison purpose, we run each algorithm ten times. For each run, the same start population was used in the same conditions (initial population, generation number and population size) for GA, BBO, MBBO and PMBBO. We measured the minimum costs (HSI for BBO versions and fitness for GA). results are in Table.3. Fig. 17. Angle error using GA, BBO and PMBBO Table 3. Minimum costs for GA, BBO, MBBO and PMBBO in 10 runs. Run GA BBO MBBO PMBBO 1 4.6e-03 4.5e-03 4.5e-03 4.2e-03 2 4.7e-03 4.5e-03 4.6e-03 4.2e-03 3 4.7e-03 4.3e-03 4.2e-03 4.1e-03 4 4.7e-03 4.2e-03 4.2e-03 4.1e-03 5 4.6e-03 4.2e-03 4.4e-03 4.1e-03 6 4.6e-03 4.3e-03 4.3e-03 4.1e-03 7 4.7e-03 4.3e-03 4.2e-03 4.0e-03 8 4.6e-03 4.3e-03 4.3e-03 4.1e-03 9 4.7e-03 4.3e-03 4.2e-03 4.1e-03 10 4.8e-03 4.2e-03 4.2e-03 4.1e-03 σ 4.8e-03 4.2e-03 4.2e-03 4.1e-03 Table 4. Performances of the PID controlled inverted pendulum GA and PMBBO. Run PMBBO GA Min HSI Tr(s) Ts(s) Omax Min fitn Tr(s) Ts(s) Omax 1 0.579 0.061 0.160 0.012 0.619 0.056 .465 0.014 2 0.579 0.064 0.175 0.012 0.592 0.058 .158 0.014 3 0.577 0.064 0.194 0.014 0.672 0.059 .783 0.018 4 0.577 0.064 0.172 0.011 0.646 0.056 .175 0.020 5 0.575 0.064 0.178 0.012 0.670 0.055 .730 0.020 6 0.581 0.065 0.208 0.015 0.632 0.077 .301 0.008 7 0.579 0.064 0.180 0.012 0.640 0.068 .117 0.014 8 0.581 0.064 0.191 0.014 0.602 0.061 .167 0.013 9 0.580 0.066 0.197 0.014 0.634 0.058 .360 0.011 10 0.568 0.065 0.178 0.012 0.606 0.060 .164 0.013 σ 0.003 0.027 D.Impact of hunt rate values and predators number in PMBBO 1. Hunt rate 2. Prrdators’ number: To study the influence of the hanut rate ρ over the PMBBO approach, several runs were carried out with the proposed variable hunt rate in (12) and different hunt rate from 0 to 1 with step of 0.1. Results are in Table.5 where minimum HSI values using (18a) and performances of the controlled system are presented, the last row is for the variable hunt rate in Equation (12). It is clear from the Table that the variable hunt rate leads to the minimum value of the cost function (HIS) (4.09e-03). When applied the obtained gains to control the inverted pendulum, best perdormances are obtaind ( settling time,n rising time and overshoot). To choose the the appropriate predators’ number, we carried out 10 runs of the PMBBO algortithm for each chosen predators number from 1 to 7. Results of the minimum value of the HIS (18a) are summerized in Table.6. The mean square value of the 10 runs are in the last row. Performances of the PID controlled inverted pendulum are in Table.7 where MSE is the mean square angle error of the pendulum . Table.6 and table.7 show that the adequate number of predators is 4 in our problem. Table 5. Performances of the PMBBO with variable hunt rates ρ HSI Tr(s) Ts(s) Omax 0.1 4.16e-03 7.64e-02 0.105 1.13e-02 0.2 4.16e-03 7.26e-02 0.099 1.41e-02 0.3 4.13e-03 4.88e-02 0.106 1.48e-02 0.4 4.13e-03 4.88e-02 0.106 1.49e-02 0.5 4.16e-03 7.08e-02 0.097 1.53e-02 0.6 4.17e-03 7.05e-02 0.152 1.59e-02 0.7 4.18e-03 4.90e-02 0.107 1.40e-02 0.8 4.15e-03 7.04e-02 0.096 1.53e-02 0.9 4.20e-03 6.94e-02 0.095 1.52e-02 1 4.18e-03 7.03e-02 0.151 1.60e-02 (12) 4.09e-03 4.28e-02 0.090 1.33e-02 Table 6. Minimum HSI for PMBBO by Predators number Run Predator number 1 2 3 4 5 6 7 1 0.6427 0.6314 0.6338 0.6132 0.6314 0.5908 0.6448 2 0.6159 0.6264 0.6414 0.6460 0.6313 0.6387 0.6438 3 0.6444 0.6438 0.6454 0.6356 0.5954 0.6466 0.6162 4 0.6427 0.6408 0.6389 0.6073 0.6417 0.6460 0.6458 5 0.6126 0.6408 0.6476 0.6280 0.6508 0.6416 0.6376 6 0.6437 0.6339 0.6385 0.6004 0.6462 0.6394 0.6090 7 0.6484 0.6496 0.6416 0.6414 0.6478 0.6487 0.6415 8 0.6277 0.6237 0.6515 0.6402 0.6474 0.6390 0.6430 9 0.6627 0.6438 0.6321 0.6534 0.6451 0.6460 0.6581 10 0.5951 0.6181 0.5998 0.6429 0.6158 0.6383 0.6040 mean 0.6336 0.6352 0.6371 0.6308 0.6353 0.6375 0.6344 Table 7. Inverted pendulum performances by Predators number Predators number HSI Tr(s) Ts(s) Omax MSE 1 0.5951 0.0752 0.1095 0.0060 7.4e-03 2 0.6181 0.0683 0.1583 0.0091 7.1e-03 3 0.5998 0.0770 0.1144 0.0060 7.5e-03 4 0.5804 0.0771 0.1012 0.0052 7.0e-03 5 0.5954 0.0772 0.1153 0.0054 7.5e-03 6 0.5908 0.0751 0.1092 0.0058 7.4e-03 7 0.6040 0.0790 0.1192 0.0060 7.7e-03 VII. CONCLUSION We presented in this paper a PID tuning method using the enhanced Biogeography based optimization. The BBO was enhanced by two major modification: A new migration operator to share better the good feaures between islands and the mutation operator was replaced by a predator and prey model to improve its diversification process. The SIVs of the algorithm are the three gains (Proportional, Integral, and Derivative). We tested our approach to control a mass spring damper nonlinear system and an inverted pendulum with good performances for the two nonlinear systems. A comparison of the proposed enhanced approach with BBO and genetic algorithms where it gives the same result or better then genetic algorithms to tune a PID controller for nonlinear systems. The proposed variable predators number formula seems to work better.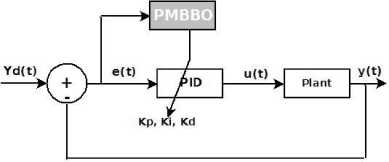

Список литературы Predator and Prey Modified Biogeography Based Optimization Approach (PMBBO) in Tuning a PID Controller for Nonlinear Systems
- D. Simon, Biogeography-based optimization, IEEE Transactions on Evolutionary Computation, 12(6), 702-713, 2008.
- M.R. Lohokare, S.S. Pattnaik, B.K. Panigrahi, and S Das, Accelerated biogeography-based optimization with neighborhood search for optimization, Applied Soft Computing, 13 (5), 2318-2342, 2013.
- H. Ma, and D. Simon, Blended biogeography-based optimization for constrained optimization. Engineering Applications of Artificial Intelligence, 24 (3), 517--525 , 2011
- H. Ma, D. Simon, M. Fei and Z. Xie, Variations of biogeography-based optimization and Markov analysis, 2013. Information Sciences, 220, 492-506, 2013.
- M.M. Sayed, M.S. Saad, H.M. Emara, and A.E.E. El-Zahab, A Novel Method for PID Tuning Using a Modified Biogeography-Based Optimization Algorithm, In: 24th Chinese Control and Decision Conference (CCDC),23-25 May 2012, Taiyuan, China, 2012
- M.A.C. Silva, L.dos S Coelho and R.Z. Freire, Biogeography-based Optimization approach based on Predator-Prey concepts applied to path planning of 3- Technologies and Factory Automation (ETFA),13-16 Sept. 2010, Cracow, Poland ,1-8 , 2010
- M.Higashitani, A. Ishigame, K.Yasuda, Particle Swarm Optimization Considering the Concept of Predator-Prey Behavior, IEEE Congress on Evolutionary Computation (CEC), 16-21 Jul 2006,Vancouver, Canada,434-437, 2006.
- M.A. Johnson and M.H. Moradi, PID Controllers: New Identification and Design Methods. Springer, 2005.
- T.K. Teng, J.S. Shieh and C.S. Chen, Genetic algorithms applied in online auto tuning PID parameters of a liquid-level control system, “Transaction of the Institute of Measurement and control, 25(5), 433-450, 2003.
- L. Fan, and E.M. Joo, Design for Auto-tuning PID Controller Based on Genetic Algorithms, In: 4th IEEE Conference on Industrial Electronics and Applications (ICIEA 2009), 25-27 May 2009, Xian, China, 2009.
- I. Chiha, N. Liouane, and P. Borne, Tuning PID Controller Using Multiobjective Ant Colony Optimization, Applied Computational Intelligence and Soft Computing, 2012.
- Y.B. Wang, X. Peng and B.Z. We, A new particle swarm optimization based auto-tuning of PID controller, Seventh International Conference on Machine Learning and Cybernetics, 12-15 Jul. 2008, Kunming, China, 2008.
- M.I. Solihin, L.F. Tack and M.L. Kean, Tuning of PID Controller Using Particle Swarm Optimization (PSO), International Conference on Advanced Science, Engineering and Information Technology, Selangor, 14-15 Jan. 2011, Kuala Lumpur, Malaysia, 2011.
- M. Salem and M.F. Khelfi, Application of Biogeography based optimization in tuning a PID controller for nonlinear systems, IEEE International Conference on Complex Systems (ICCS), 5-6 Nov 2012, Agadir, Morocco, 2012.
- A. Bagis, Determination of the PID Controller Parameters by Modified Genetic Algorithm for Improved Performance, journal of information science and engineering, (23), 1469-1480, 2007.
- H. Kundra, A. Kaur and V. Panchal, An integrated approach to biogeography based optimization with case based reasoning for retrieving groundwater possibility, in: 8th Annual Asian Conference and Exhibition on Geospatial Information, Technology and Applications, 18-20 Aug. 2009, Singapore, 2009.
- X. Li, A real-coded predator-prey genetic algorithm for multiobjective optimization, Evolutionary Multi-Criterion Optimization Lecture Notes in Computer Science, 2632, 207-221, 2003.
- M. Ovreiu, and D. Simon, Biogeography-based optimization of neuro-fuzzy system parameters for diagnosis of cardiac disease, In: Genetic and Evolutionary Computation Conference, Portland, Oregon, USA, 1235-1242, 2010.
- V. Panchal, P. Singh, N. Kaur, and H. Kundra, Biogeography based satellite image classification. Int. J. of Comp. Sci. and Info. Security, 6, 269—274, 2009.
- D. Simon, A dynamic system model of biogeography-based optimization, Appl. Soft Comput. 11(8), 5652-5661, 2011.
- A.A. Aly, Model Reference PID Control of an Electro-hydraulic Drive, International Journal of Intelligent Systems and Applications (IJISA), Vol.4 No.11, October 2012.
- S. Sharma, V. Kumar, R. Kumar, Supervised Online Adaptive Control of Inverted Pendulum System Using ADALINE Artificial Neural Network with Varying System Parameters and External Disturbance, International Journal of Intelligent Systems and Applications(IJISA),Vol.4, No.8, July 2012.


