Предельно-квазистационарная модель электрохимического формообразования

Для математического моделирования процесса электрохимической обработки (ЭХО) используются законы Фарадея и Ома. В соответствии с этими законами скорость растворения равна V ecm = k n E , E = j J к , k = к/ p , где E , j - напряженность и плотность тока на границе анода; к -электропроводность электролита; n = П ( j ) — выход по току; г - электрохимический эквивалент; р

- плотность растворяемого материала.

Рассматривается ЭХО в пассивирующем электролите с круто падающей до нуля при уменьшении плотности тока зависимостью n(j)• В [1-3] рассматривались стационарные и квазиста- ционарные процессы, для этого использовалась ступенчатая зависимость

П о ,

П ( j ) = П ф Л о ] ,

j >  ^j\„ j = j ) ,

0, j <  j ) .

В данной работе проводится исследование нестационарных процессов с помощью квазиста-ционарной модели. Рассматриваются процессы с предельно высокой локализацией, при этом максимальное значение плотности тока на обрабатываемой поверхности E ₀ равно критическому

E ₁ = j₁ К • Аналогичные задачи для других конфигураций электрод-инструментов (ЭИ) рассмотрены в [2].

Будем считать электрическое поле в межэлектродном пространстве (МЭП) соленоидальным и потенциальным. Тогда задачу определения напряженности поля можно решать с помощью аналитических функций комплексного переменного.

Задача формообразования при обработке пластинчатым электрод-инструментом

Рассмотрим задачу обработки угловой поверхности ЭИ в виде пластины A CB ‘ с изолированной верхней поверхностью, которая движется горизонтально вправо с постоянной скоростью V et . Формы межэлектродного пространства (МЭП) до и в процессе обработки показаны на рис. 1.

На плоскости комплексного потенциала образом МЭП является полуполоса шириной U (рис. 2, а ).

При использовании зависимости выхода по току (1) и условия E0 = E1 на обрабатываемой поверхности образуются две зоны, в одной из которых происходит растворение, в другой - отсутствует. В первой зоне FMNG модуль напряженности равен E1. На плоскости E = dW/dZ = |E|ei8 этой зоне соответствует дуга окружности радиуса E1 с центром в начале координат. Участкам AF (0 = 0) и GB (0 = -П2}, где отсутствует растворение, на плоскости E соответствуют отрезки, соответственно, действительной AF и мнимой GB осей.

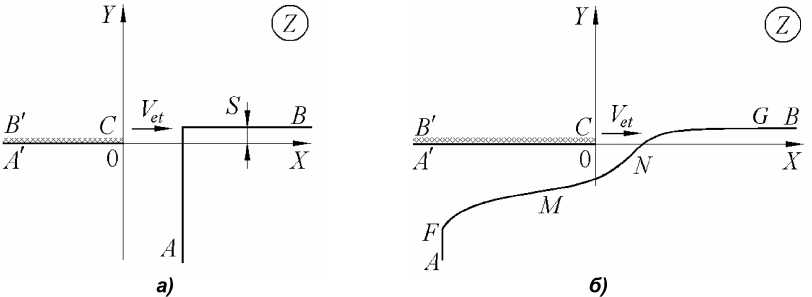
Рис. 1. Формы МЭП на физической плоскости: а) перед началом процесса; б) в процессе обработки. FMNG – зона критического значения напряженности E 1 ; AF , GB – нерастворяемые границы

На поверхности ЭИ A C угол 0 = -П 2, на B C 0 = п . Поэтому на плоскости годографа E имеем, соответственно, вертикальный и горизонтальный лучи. Область на плоскости годографа размещается на двулистной поверхности. Для наглядности можно изобразить каждый лист отдельно (рис 2, б , в ).

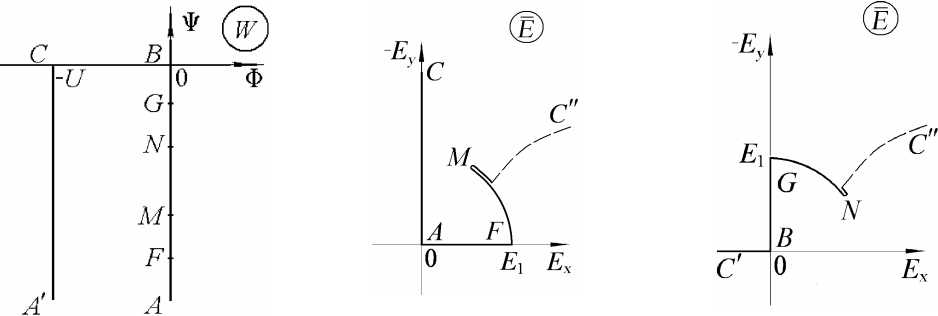
a                               б                               в

Рис. 2. Образы МЭП на плоскостях: а) комплексного потенциала; б) , в) годографа; б) первый лист; в) – второй лист

Применив преобразование Жуковского

EE to = i ln— = 0 + i T , т = In   ,

E 1                 E 1

получим фигуру, граница которой содержит только части прямых, т.е. многоугольник с углами A , B , C , F , G , M , N , равными 0; 0; 0, П 2; П 2; 2 п , 2 п соответственно (рис. 3, а , б ).

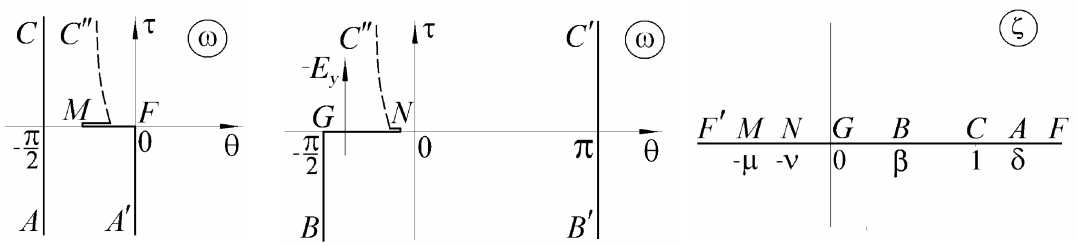
a)                                    б)                                    в)

Рис. 3. Образы МЭП на плоскостях параметрического переменного: а) первый лист плоскости ω ; б) второй лист плоскости ω ; в ) плоскость ζ

Для получения функции, конформно отображающей верхнюю полуплоскость Z (рис. 3, в) на этот многоугольник, используем преобразование Шварца–Кристоффеля

w ( Z ) = с Z                        ,

1 i ( Z - 5 )( Z - в )( Z - 1 ) Z ¹²

Имеем

( Z + А )( Z + v )    = ( 5 + ц )( 5 + v ) 1 + ( в + A )( в + v ) 1 ₊ ( 1 + A )( 1 + v ) 1

( Z - 5 )( Z - в )( Z - 1 ) ( 5 - в )( 5 - 1 ) Z - 5 ( в - 5 )( в - 1 ) Z - в ( 1 - 5 )( 1 - в ) Z - 1,

I

d Z

( Z - 5 ) V ?

u = Z

Я dZ dU =

2 V Z

= ₂f du

~ ' u ² - 5

1 u - 5 = -j=ln---- i=

5 u + 5

= ^ln 5

Z - 5

Z + 5

Тем самым

_{w ( Z )} = C Z    ( Z + a )( Z + v ) d Z   = С ( 5 + a )( 5 + v ) J. Z - 5 ₊

^{И   1} i ( Z - 5 )( Z - в )( Z - O Z ^{12   1} ( ⁵ - в )( ⁵ - 1 ) 5 Z + 5

(в+a)(в+v) Z - в. Г wmitv

I C^                                       in.                    I C^                            in..

1 (в - 5)(в -1) в Z + в   (1 - 6)(1 - в)

Поскольку в соответствии с рис. 3

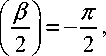
_ ( 1 + в )     _D ( 1 + 5

Re w —— = n , Re w---

I 2 J I 2

n

2, то

Re w ' ^{1+ 5} ) = С

( 2 J ¹

( 5 + ц )( 5 + v ) 1

( 5 - в )( 5 - 1 ) 5

i n =

n

-

,

С 1

( 5 + ц )( 5 + v ) 1 _i_ ( 5 - в )( 5 - 1 ) 7 5 " 2,

D ( ¹ + в

Re w ——

I 2

= C

( 5 + ц )( 5 + v ) 1

( 5 - в )( 5 - 1 ) 5

i n + C 1

( 1 ⁺ ц )( 1 ^{+ v} ) ^{( 1 - 5 )( 1 - в )}

i n = n

—in + C 2 ¹

( 1 ⁺ ц )( 1 ^{+ v} ) ^{( 1 - 5 )( 1 - в )}

i n = n

( 1 ⁺ ц )( 1 ^{+ v} ) ₌ 3

1 (1 - 5)(1 - в)

Re w

= С 1

( ^{5 +} a )( ^{5 + v} ) 1         ( 1 ⁺ A )( 1 ^{+ v} )       ( ^{в +} A )( ^{в + v} ) 1 . _ n

П + C i              -in + C i                  i = ITT = ,

( 5 - в )( 5 - 1 ) 5     ¹ ( 1 - 5 )( 1 - в )      ¹ ( в - 5 )( в - 1 ) в 2,

• i .    .3. ^( в + А)(в + v) 1 .     п  (в в + А)(в + v) 1.3

in - г in + C1-,-^m = , C1-, = I

• 2     2     1 (в - 5)(в -1) в     2   1 (в - 5)(в -1) в

Из (5), (6) и (7)

С = i 45 ( 5 - в )( 5 - 1 )

¹     2 ( 5 + a )( 5 + v ) ,

5 (5-в)(5-1) (1 + А)(1 + v) =- 3  5 (5-в)(1 + А)(1 + v)

2 (5 + a )(5 + v ) (1 - 5)(1 - в)    2,  2 (5 + a)(5 + v )(1 - в)

5 ( 5 - в )( 5 - 1 ) ( в + А )( в + v ) 1 = 3   5 ( 5 - 1 )( в + А )( в + v ) 1 =- 3

• 2 (5 + a )(5 + v )(в - 5)( в -1) в 2, 2 (5 + ц )(5 + v)( в -1) #

  
  

Если точки перегиба M и N отсутствуют, то параметры ц и v - комплексно сопряженные, (т.е. ц = ц 1 + i v 1 , v = ц 1 - i v 1 ). Тогда уравнения (9), (10), примут вид

7 5 ( ^{5 - в} ) ( ( 1 ⁺ А 1 ) 2 ^{+ v}" ) = 3

² ( 1 - ^в ) ( ( ^{5 +} А 1 ) ^{2 + v} 1² ) ²

75 (5—1)((в+а )2 'г) 1 _ з

f) в 2.

Тем самым с учетом (5)–(7), окончательно

Согласно (2)

( Z ) _ i ln

+ i —In

— i — In

— I dW

E _---_ E,e dZ 1

i to	Z — 5
- E '^	Z +V 5

.

7

V V b ¹7

С учетом (13)

dZ _ — eltodW _

E 1

1	Z +'	5
E 1	У У	5

7

w ь ⁺

dW

Z ^{d Z} .

Теперь с помощью преобразования Шварца-Кристоффеля найдем функцию W ( Z ) ^{W (Z)_ C 2} в ( Z — 5 )( Z — в ) ¹² ( Z — 1 ) ¹'²"

C 1 ln

4 ( 5 — в )( 5 — 1 )

[ y< 5 — 1 >« — в ) — У( 5 — в )( Z — i ) ] 2 ^Z _

z—5

в

_ C 2

( 1 — в )( Z — 5 )

1 ln

Vt ⁵ ^ )! ^{5 3} ! )   [ V ( 5 — 1 )( Z — в ) + J( 5 — в )( Z — 1 ) ]

При обходе точки Z = 5 по полуокружности малого радиуса против часовой стрелки действительная часть W получает приращение, равное - U , логарифм - приращение мнимой части i п . Отсюда

Л Re W _ - U _ C ,    ¹      i n .

2 4(5—в)(5—1)

Тогда

C 2 _ iU ( 5 — в )( 5 — 1 ) . n

Тем самым, окончательно

W ( Z ) _ iU ln

n

( 1 — в )( Z — 5 )             .

[ 7 (5—1)(z—в)+4 (5—в)(z—1) ]2

Производная

dW U   7(5 — в)(5 — 1)

----T" _ i--"------,                -------- .

dz   n (z—5) У (z—в )(z—1)

Из (15) и (18)

dZ _ iU Z( 5 — в )( 5 — 1 )

(Z+V5)(yz+Ув)3

Z — 1

( Z — 5f-  ( Z — в ) ² (J Z + 1 ) 3

d Z .

Интегрируя (19) численно от Z = 1, получим функцию Z ( Z ) •

Параметры заглубления кромки ЭИ L и S определяются следующим образом

Шерыхалина Н.М., Зарипов А.А., Поречный С. С.

Предельно-квазистационарная модель электрохимического формообразования

L = - Re Z ( - ) , 5 = Im Z ( 0 ) ,                              (20)

E безразмерное время т = Lu1.

На рис. 4 приведены формы обрабатываемой поверхности в неподвижной относительно материала заготовки и подвижной (связанной с кромкой ЭИ) системах координат, соответствующие 5 = SE- = 0 и т = - 2; - 1,5; - 1; - 0,5; 0; 0,5; 1; 1,5; 2;...; 5.

U

На рис. 4, а при т ^ ^ видно установление предельно-стационарной конфигурации с |E = E 1 . Вблизи нерастворяемой зоны AF при возрастании т формируется некоторая предельная форма (рис. 4, б , кривая ^ ). Эта форма соответствует решению задачи об истечении из-под щита [4]. Известно, что эта кривая является гладкой, но ее кривизна в точке перехода к прямой равна бесконечности.

Следует отметить, что при т < 0 образы точек перегиба -ц и -V совпадают и при дальнейшем уменьшении т становятся комплексно сопряженными (обозначим их ц = Ц 1 + i v 1 , V = Ц 1 - V (11),

(12)). При этом внутри области на плоскости E появляется точка ветвления M , являющаяся образом точки Z = -Ц + i u . Линия «склейки» на плоскости E начинается с некоторой точки на границе области, проходит через точку ветвления, разворачивается и уходит на бесконечность (рис. 5). Как видно из рис. 4, б , при т ^ -^ длина обработанной части поверхности уменьшается и стремится к нулю.

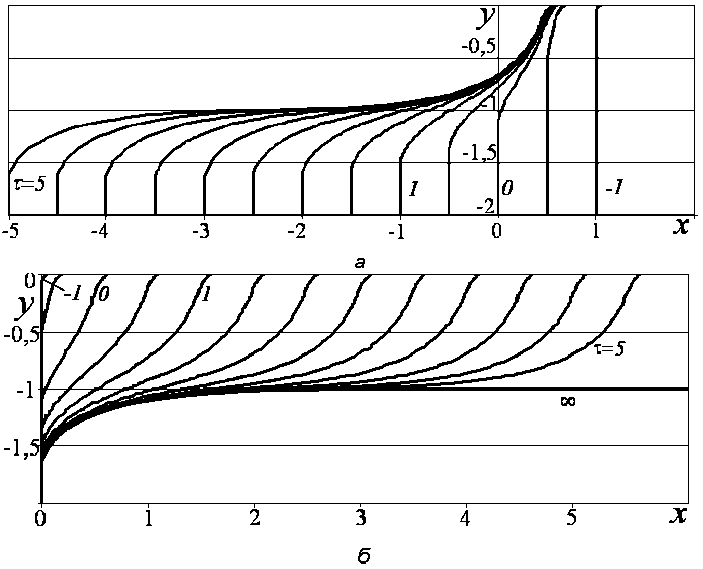
Рис. 4. Формы обрабатываемой поверхности для s = 0: а) в системе координат, связанной с кромкой ЭИ C (0,0); б) в неподвижной системе координат

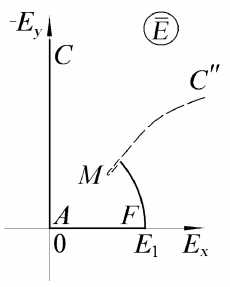
а

Рис. 5. Образ МЭП на плоскости годографа: а) первый лист; б) второй лист

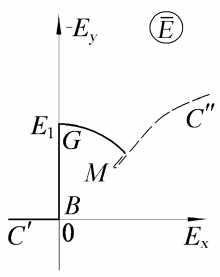
б

Выводы

Таким образом, в квазистационарном приближении решена плоская задача обработки горизонтальным пластинчатым электрод-инструментом с изолированной верхней поверхностью заготовки, имевшей до обработки угловую форму. Как показывают численные исследования [5], в таких задачах квазистационарное приближение весьма точно (до 3–4 значащих цифр) приближает нестационарное решение.