Предсказание нелинейного эффекта для анизотропии питч-углового распределения заряженных частиц на геостационарной орбите

Геостационарная орбита. (ГСО) космического аппарата, расположена в плоскости географического экватора, па. расстоянии около 36 тыс. км от поверхности Земли в области внешнего естественного радиационного пояса Земли (ЕРПЗ). Это соответствует магнитной оболочке L « 6,6 (L - параметр Мак-Илвейна). В плоскости геомагнитного экватора магнитная оболочка L удалена от центра Земли на расстояние равное LR_e, г де R e - средний радиус Земли.

Питч-угловое распределение заряженных частиц, т.е. зависимость дифференциального потока, частиц 3 от локального питч-угла частиц а в диапазоне от 0° до 180°, - это важная характеристика заряженных частиц в пространстве скоростей в магнитосфере Земли, в частности для радиационных поясов, кольцевого тока, и геостационарной орбиты.

Питч-угловые распределения типа, “бабочка” (англ, “butterfly”) - это такие распределения, у которых для питч-угла. 90° наблюдается локальный минимум, а. симметрично от пего слева, и справа. - два. одинаковых по величине максимума. Значительно чаще встречаются нормальные (англ, “normal or pancake”) питч-угловые распределения, так называемые потому, что максимальные потоки в этом случае для питч-угла. 90°. Другие типичные питч-угловые распределения следующие: изотропные или плосковершиппые (англ, “isotropic or flattop”) и типа, “голова, и плечи” (англ, “head and shoulders or cap”).

В монографии [1] для описания всех встречающихся в магнитосфере питч-угловых распределений было предложено для использования следующее распределение

3 (а) = З е sin^7H а, (1)

^гД^е З е - перпендикулярный дифференциальный поток заряженных частиц (а = 90°).

Уравнение (1) отличается от общепринятого тем, что индекс анизотропии (или показатель) питч-углового распределения не есть постоянная величина (7 = const), а является функцией от а (7 = 7 ^(а)).

Для диапазона питч-углов 0° < а < 90° 7 (а) можно найти по формуле

/ х 1g ^{3 (а) -} 1g З е

7 (а) = ---;—:------

1g sin а

Для а = 90° уравнение (2) дает отношение 0/0, поэтому находим предел 7 при а ^ 90°, используя правило Лопиталя,

- 3Е (S ъ

7 е =

При проведении практических расчетов для 71 хорошим приближением является следующая фор мула

7± = 7 (870) =

lg j (870) - lg j± lg sin 870

.

Перпендикулярный индекс анизотропии (показатель) питч-углового распределения 7^, представленный в общем виде формулой (3), является точным индикатором типа, питч-углового распределения и в этом его большая ценность. Конкретно, если питч-угловые распределения нормальные или типа “голова и плечи”, то вторая производная по а от дифференциального потока частиц для питч-угла 90° меньше 0, поэтому с учетом того, что всегда j^ > 0, из (3) получаем 7^ > 0. Если 7^ = 0, это уже будет соответствовать изотропному или плосковершинному питч-угловому распределению. И наконец, питч-угловые распределения типа, “бабочка”. В этом случае вторая производная по а от дифференциального потока частиц для питч-угла 90° больше 0 и поэтому из (3) получаем 7^ < 0. Такое представление (3) является точным при определении момента появления питч-углового распределения типа, “бабочка”. В отличие, например, от общепринятого, когда определяется некое среднее значение 7 = const для почти всего диапазона питч-углов (от 0° до 180°) и при этом игнорируются очень маленькие положительные, а. иногда, даже маленькие отрицательные значения 7^.

Из представленного следует, что математическая модель для анизотропии питч-углового распределения заряженных частиц должна, описывать все четыре типа, питч-угловых распределений вместе с их вариациями.

Литература, по питч-угловым распределениям заряженных частиц и анизотропии питч-угловых распределений обширна. Например, моделирование питч-углового распределения на. дневной стороне магнитосферы Земли рассматривалось в [2], а. на. ночной стороне магнитосферы - в [3]. В работе [4] была, предложена, двумерная феноменологическая модель динамики кольцевого тока, в магнитосфере Земли (PheMRC 2-D). В этих трех работах численно решалось уравнение питч-угловой диффузии в диапазоне питч-углов от 0° до 180°и поэтому только численно определялся перпендикулярный ( а = 90°) индекс анизотропии питч-углового распределения заряженных частиц (протонов). В [5] был представлен статистический анализ питч-углового распределения энергичных электронов радиационного пояса, около геостационарной орбиты: наблюдения спутника. CRRES с определением индекса, анизотропии питч-угловых распределений. Обзор анизотропии внешнего электронного радиационного пояса, во время магнитных бурь, управляемых высокоскоростным потоком частиц солнечного ветра, представлен в [6]. Эмпирическая модель питч-угловых распределений для энергичных электронов (REPAD) во внешнем радиационном поясе Земли была, предложена, в [7]. В [8] подробно рассмотрено статистическое измерение количества, питч-углового рассеяния, которому подвергаются энергичные электроны, когда, они дрейфуют поперек плазмо-сферпого “пера.” стока, (англ, “plasmaspheric drainage plume”) па. геосинхронной (геостационарной) орбите. Статистика, и поведение протонного и электронного радиационных поясов во время магнитных бурь, управляемых высокоскоростным потоком частиц солнечного ветра, на. геосинхронной орбите представлены в [9]. В [10] определен состав ионов внутренней магнитосферы как функции энергии и магнитного местного времени для полного солнечного цикла, с 2001 г. по 2013 г. с указанием индекса, анизотропии. А в [11] предложена другая эмпирическая модель питч-угловых распределений электронов радиационных поясов, основанная па. измерениях зондов Ван Аллена, с примерами разных типичных питч-угловых распределений. Из всего обзора, за. последние годы видно, что статистические и эмпирические модели анизотропии питч-углового распределения заряженных частиц есть, а. аналитических математических моделей, основанных на. физике и описывающих индекс анизотропии питч-углового распределения заряженных частиц, вероятно, пет.

Поэтому целью данной работы является математическое моделирование индекса, анизотропии питч-углового распределения заряженных частиц на. геостационарной (геосинхронной) орбите в магнитосфере Земли в виде: 1) повой математической модели, основанной на. физике и опись:- вающей перпендикулярный индекс анизотропии питч-углового распределения заряженных частиц на ГСО в зависимости от местного времени LT на ГСО и Кр - индекса геомагнитной активности и 2) анализа, следствий предложенной аналитической модели.

• 1. Математическая модель

В первом приближении зависимость перпендикулярного индекса, анизотропии питч-углового распределения заряженных частиц от времени 7±(t) найдем из уравнения d7^   ^7± dL dt    dL dt

Для вычисления d^/dL используем [12, 13] для приближенного описания

7_± = к, 73,75

/     ,—\ 0,1

( QVE)

L2,74

где размерность Q - в единицах 10^-19 [м²], а размерность энергии Е - в [кэВ]. Безразмерный коэффициент к, отсутствует в [12, 13], но здесь он вводится в (6) для наилучшего согласия при сравнении с конкретными экспериментальными данными.

Для примера, возьмем эффективное сечение перезарядки нейтрального водорода, и протона. Q, которое аппроксимируется выражением

Q = 3,27 (Е Г exp (- (Е0 Г),                    (7> где Е0 = 1.76 кэВ.

Сравнение (7) с экспериментальными величинами, как это представлено в работе [14], показывает превосходное согласие для энергий ниже 300 кэВ. Для больших энергий спад эффективного сечения уменьшается быстрее, чем предсказано (7).

При проведении численных расчетов будем полагать в уравнении (5), что dL/dt и ^dL/dt\ Тогда, баупс-усредпеппая радиальная дрейфовая скорость движения заряженных частиц в магнитосфере Земли будет определена, например для дипольного магнитного поля Земли, так [15, 1]:

{=-П 2 L4cos ф,

где t - время; ф - азимутальный угол (местное время LT = 0 ч в полночь) или геомагнитная восточная долгота в плоскости магнитного экватора; П = 24 - угловая скорость вращения Земли в 1/ч; фо = 92 кВ; а зависимость ф₂, измеренная в кВ, от геомагнитной активности, т.е. от Кр = Kp(t) - индекса, определяется по формуле [16]

0, 045

2   (1 - 0,16Кр + 0,01Кр2)3 '

Тогда, уравнение (5) с учетом (8) записывается следующим образом d7± + d7± Пф2(t)L4(t) cos ф(t) = 0

Теперь к уравнению (10) можно добавить уравнения, описывающие траекторию движения космического аппарата. (КА) в гравитационном поле Земли. Но будет еще проще, если задать траекторию КА в параметрическом виде. В этом случае для ГСО (аналогично для любой круговой орбиты) получаем

L(t) = 6, 6;     ф(t) = fit + ф,

(П)

где p = const будет определяться из сопоставления с экспериментальными данными на ГСО, a t - это уже местное время (local time) LT вдоль ГСО.

В дальнейшем, для КА с любой круговой орбитой или с эллиптической орбитой движения такую замену в (10) можно будет делать аналогично (11).

Уравнения (10), (11) представляют общую формулировку феноменологической модели предсказания динамики перпендикулярного индекса, анизотропии питч-углового распределения заряженных частиц на. геостационарной (геосинхронной) орбите в магнитосфере Земли.

В итоге, используя (6), (7), (9) - (11), получаем для Е = const, Кр = const, L = const

= АП cos(fit + p), dt где

А = k^ 202,075

( v e )^0,613    l-\

Тогда, аналитическое решение дифференциального уравнения (12), (13) будет иметь вид

7x(t) = A[sin(Qt + p) - sin p] + 7хо,

где ухо - это индекс анизотропии (показатель) питч-углового распределения заряженных частиц, взятый для питч-угла 90° и в момент местного времени t = 0ч LT.

Если Kp(t) = const и (9) ф₂ (t) = const (зависимость от t может быть сложной), получим, используя (13), величину А*

А* = k₇202,075

( qVE)

0,613 L^0,26 Фо

и следующую общую формулу для модельных (прогнозных) расчетов 7x(t) на ГСО и на любой круговой орбите КА

t

7x(t) = А* П

/

Ф2 (t) cos(Ot + p)dt + ухо.

где П 24 - угловая скорость вращения Земли в 1/ч, at- это местное время LT вдоль ГСО в часах.

Чтобы сравнить общую зависимость от местного времени 7_X(t) (17), (13) с экспериментальными данными для электронов с энергией Е = 120 кэВ ([8] рис. 8) на ГСО, произведем тестовые (модельные) расчеты для протонов (из-за. наличия эффективного сечения перезарядки (7)) с энергией Е = 120 кэВ, k₇ = 1 (в упрощенном варианте) (6), для Кр = 3- (или Кр = 2,66) и Кр = 5

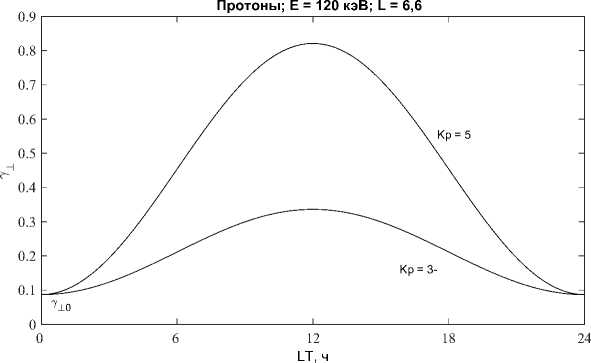
Рис. 1. Тестовые (модельные) аналитические зависимости перпендикулярного индекса анизотропии питч-углового распределения протонов с энергией 120 кэВ, к^ = 1 и а ГСО 7±(t) (17), (13) от местного времени LT и Кр - индекса геомагнитной активности. Для нижней кривой Кр = 3- , а для верхней кривой Кр = 5.

(13), (9). При этом 710 = 0,0868 (6), (7), когда t = 0 ч LT. Результаты расчетов представлены на рис. 1.

Для индекса геомагнитной активности Кр = 3 - при сравнении на качественном физическом уровне получено очень хорошее соответствие, так как по многочисленным данным ([8] рис. 8) кривые для меньших Кр = 2-3 приблизительно симметричные относительно местного полудня с максимальной анизотропией приблизительно в полдень. Однако, при более высоких Кр = 4-5,7 ([8] рис. 8) кривые очень асимметричные относительно полудня с анизотропиями сильнее в утреннем секторе, чем в послеполуденном секторе. Тогда как модельная кривая 7i(t) (17), (13) для Кр = 5 (и для Кр = 3-) на рис. 1 строго симметрична относительно местного полудня с максимальной величиной 7i(t) в полдень. Это расхождение с экспериментом на качественном физическом уровне связано с тем, что величина 7i(t) определена только в первом приближении. С другой стороны на рис. 1 модельная кривая для Кр = 5 выше кривой для Кр = 3-, что в целом соответствует экспериментальным данным ([8] рис. 8). Таким образом, общая аналитическая зависимость перпендикулярного индекса, анизотропии (показателя) питч-углового распределения заряженных частиц на ГСО 7i(t) (17), (13), полученная в первом приближении, может быть использована (особенно для магпитоспокойпых условий) для количественных прогнозов и сравнений с экспериментальными данными на. ГСО после привлечения соответствующих эффективных сечений перезарядки и кулоновских столкновений для электронов, протонов и ионов.

Используя аналитическую зависимость для перпендикулярного индекса, анизотропии (показателя) питч-углового распределения заряженных частиц на. ГСО от местного времени LT вдоль ГСО 7i(t) (17), можно определить половину ширины 5рт от такого распределения. Для этого под шириной распределения (17) будем понимать “расстояние” между местными временами LT вдоль ГСО ( t1 и t₂), соответствуют,ими “половине” 7±(t), т.е. среднему арифметическому значению двух величии: минимума 71(0) = 710 (в полночь) и максимума 71(12) (в полдень). Сформулировано по аналогии с гауссовым распределением, когда, шириной гауссовой линии называется расстояние между частотами, соответствующими половине максимальной интенсивности.

Сначала, получаем следующее уравнение

^{7 1 0} Л ^{+ 7 1 0} = Л ^[   (fit   ₂') +1] + 710,                     (18)

а после упрощения - уравнение

з^\ sin (fit + — I

= 0.

Тогда местные времена вдоль ГСО t1 и t2 находятся как корни уравнения (19) в часах LT t1 = 6, t2 = 18.

Отсюда следует, что половина ширины распределения (17) 5 lt = 6 ч LТ, когда Кр « const, например, в течение одних суток (рис. 1).

Таким образом, получено для математической модели, основанной на. физике и описывающей перпендикулярный индекс анизотропии питч-углового распределения заряженных частиц на. ГСО в зависимости от местного времени LT на ГСО и Кр - индекса геомагнитной активности (17), (13), что половина ширины (17) есть величина постоянная и не зависящая от Кр - индекса. Т.е. в рамках первого приближения это “инвариант” (па. будущее возможный или приближенный при каких-то условиях), не зависящий от А (13), что в дальнейшем заслуживает дополнительного уточнения.

Далее, для ГСО найдем модельную (прогнозируемую) разницу между максимальным значением 7^(12) (в полдень) и минимальным значением 7±(0) = 7±о (в полночь) в зависимости от Кр индекса геомагнитной активности, используя для этого (17), (13), (7) и (9). В результате получается следующее простое уравнение

7^(12) - 7±о = 2А.

Для примера проведем тестовый (модельный) расчет для протонов с энергией Е = 120 кэВ на ГСО и k^ = 1 (13), (7), (9) (т.е. в упрощенном варианте). Таким образом, получается интересная нелинейная зависимость (21), если примерно в течение одних суток Кр = const или Кр « const, которая представлена, па. рис. 2.

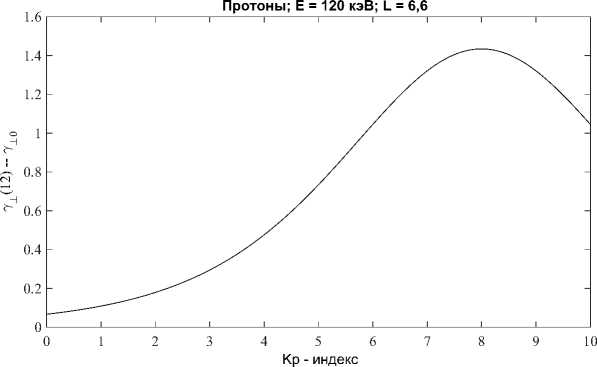
Рис. 2. Тестовая (модельная) аналитическая зависимость разности перпендикулярных индексов анизотропии питч-углового распределения протонов с энергией 120 кэВ, к^ = 1 и а ГСО уД12) — уто (21), (13) от Кр - индекса геомагнитной активности.

При этом надо заметить, что правая часть уравнения (21) зависит не только от Кр - индекса. геомагнитной активности, по и от энергии заряженной частицы и от величины эффективного сечения перезарядки (13). Поэтому разница. (21) будет меняться количественно в зависимости от величии параметров в формуле (13), по па. качественном физическом уровне нелинейная зависимость (21) от Кр не изменится. На рис. 2 для нелинейной зависимости (21) наблюдается строгая симметрия от Кр = 6 до Кр = 10 с максимумом разности 7щ (12) — 7до в 1,434 (это теоретический предел для примера) при Кр = 8. Такое теоретическое предсказание, в общем, необходимо проверить в дальнейшем по соответствующим экспериментальным данным. И еще, в уравнении (21) величина А (13) определена пока в первом приближении, ио в будущем А можно находить и уточнять по экспериментальным данным, используя уравнение (21), что будет, наверно, значительно проще.

Таким образом, полученную нелинейную зависимость (21) можно рассматривать как теоретическое предсказание нелинейного эффекта, для разности между максимальным значением перпендикулярного индекса анизотропии питч-углового распределения заряженных частиц уд(12) (в полдень) и минимальным значением перпендикулярного индекса анизотропии 7±(0) = у±₀ (в полночь) на ГСО ( L « 6,6) от Кр - индекса геомагнитной активности.

Представленный нелинейный эффект для анизотропии питч-углового распределения заряженных частиц (21), (13) будет, вероятно, в той или иной степени и на. других радиальных расстояниях от Земли, т.е. при других значениях параметра Мак-Илвейна L.

Заключение

Предложена, новая феноменологическая модель предсказания динамики перпендикулярного индекса, анизотропии питч-углового распределения заряженных частиц на. геостационарной (геосинхронной) орбите (ГСО) в магнитосфере Земли, а. также на. любой круговой орбите в зависимости от местного времени LT на орбите и Кр - индекса геомагнитной активности.

Проведено сравнение модели на. качественном физическом уровне с многочисленными экспериментальными данными, полученными с 1999 г. по 2007 г. Доказано, что общая аналитическая зависимость перпендикулярного индекса, анизотропии питч-углового распределения заряженных частиц на. ГСО, полученная в первом приближении, может быть использована, (особенно для магнитоспокойных условий) для количественных прогнозов и сравнений с экспериментальными данными на. ГСО после привлечения соответствующих эффективных поперечных сечений перезарядки и кулоновских столкновений для электронов, протонов и ионов.

Получено для предложенной математической модели, что половина, ширины общей аналитической зависимости от местного времени LT на орбите 5 _lt = 6 ч LТ (когда Кр « const, например, в течение одних суток) есть величина постоянная и не зависящая от Кр - индекса.

Теоретически предсказан нелинейный эффект для разности между максимальным значением перпендикулярного индекса, анизотропии питч-углового распределения заряженных частиц (в местный полдень LT = 12 ч) и минимальным значением перпендикулярного индекса, анизотропии (в местную полночь LT = 0 ч) на ГСО от Кр - индекса геомагнитной активности.

Нелинейный эффект для анизотропии питч-углового распределения заряженных частиц будет, вероятно, в той или иной степени и на. других радиальных расстояниях от Земли.