Представление функции Грина бигармонической задачи Навье

Введение . Явный вид функций Грина для разных эллиптических краевых задач приводится во многих исследованиях. Например, в двухмерном случае, в работе [1], на основании известной гармонической функции Грина представлены функции Грина различных бигармонических задач. Явный вид функции Грина в секторе для бигармонического и 3-гармонического уравнений найден в работах [2, 3], а в [4–6] приведен явный вид функций Грина задачи Дирихле для этих же уравнений в единичном шаре. В работе [7] на основании интегрального представления функций класса u g C ⁴( D ) n C ³( D ) даются интегральные представления решений задач Навье и Рикье-

Неймана для бигармонического уравнения в единичном шаре, а также строятся функции Грина этих задач.

В настоящей заметке будет найдено новое представление функции Грина задачи Навье для бигармонического уравнения в единичном шаре с явно выраженной сингулярностью, а также будет дано новое представление решения задачи Навье для однородного бигармонического уравнения без явного использования функции Грина.

Хорошо известно, что функция Грина задачи Дирихле для уравнения Пуассона в шаре

S = { x g I n : | x | < 1} при n >  2 имеет вид G ₂ ( x , % ) = E ( x , % ) - E* ( x , % ), где E ( x , % ) - элементарное

I X              1

решение уравнения Лапласа [8] и E (x, %) = EI —,| x | % I. По аналогии с этим в работе [4] было определено элементарное решение бигармонического уравнения

E 4( X , О Ч

2( n - 2)( n - 4) ^- 4 ^{x -} % ^|,

| x -% | ^{4 - n} ,   n >  4, n = 3

n = 4      ,

I x -% | ²

.    4

и доказано, что при n >  3 функция вида

n = 2

G 4 ( x , % ) = E 4 ( x , % ) - E ₄ * ( x , % ) - x 2   ¹ ЧЧ E ’( x , % ) ,

где

E * ( x , % ) = E 4

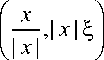
является функцией Грина задачи Дирихле для бигармонического

уравнения в шаре S , удовлетворяющей равенствам G ₄ ( x , % ) | %_{Gd S} = 6 G ₄ ( x , % ) / dv | %_{Gd S} = 0 при x g S . В случае n = 2 последнюю строчку в формуле (1) нужно слегка подправить: вместо - 1 надо взять - 1/2.

Математика

Задача Навье [9, 10] для бигармонического уравнения (в [1] она называется задачей Дирихле-

• 2)    заключается в нахождении функции u е C ⁴( S ) n C ³( S ) , являющейся решением следующей граничной задачи:

A ² u ⁽ x ) = f ⁽ x ), x е S ,   u | _{5 5} = ф ₀, A u | _{a 5} = фр                           ⁽³⁾

В работе [4, теорема 2] установлено, что функция Грина задачи Навье (3) находится по формуле

G n ( x ,О = — f G 2 ( x , y ) G 2 ( y , % ) dy ,                            (4)

®n JS где ©и - площадь единичной сферы. Характер сингулярности у функции Gn (x, %) здесь явно не виден. Поэтому дадим другое представление функции Грина задачи Навье, похожее на формулу (2).

Представление функции Грина. В дальнейшем изложении будет необходим следующий n оператор Лu = ^ xkuxk.

k = 1

Теорема 1. 1) Функция g n ( x , % ), определяемая равенством

Q n’ ( x , ^ ) = £ 4 ( x , % ) - E * ( x , ^ ) - ^ x ^ Ш2- -■ f¹ E * ( x, t % ) t ^{n /2 - 1} dt,                (5)

2      2 J0

где x ^ %e S , является бигармонической по % ^ x е S и удовлетворяет равенствам

• 4    ⁽ x , О ^| %ед S = ^A ^^4 ⁽ x , ^ ) ^| %ed S = ⁰ при x ^{G S} .

• 2)    Если функция u е C ⁴ ( S ) n C ³ ( S ) является решением задачи Навье (3), то она может быть

представлена в виде

1 f ^dA%^ n ^{( x} , % )             1 г эд n ( x , % )             1г

• u ( x ) = —   —4-----Фо ( % ) ds _§ +-- -------ф 1 ( % ) ds % +-- £4 ⁽ x , % ) f ( % ) d %. .     ⁽⁶⁾

• ю_и    ^JSS     dv                ю_и ^JSs dv              ю_л ^Js

Доказательство. 1) Бигармоничность функции E ₄( x , % ) при x ^%е S и функции E * ( x , % )

при x, % е S была установлена в [4, теорема 2.2]. Известно также, что функция E*(x, t%) - гармо ническая при x, % е S , а значит, функция (| x |2 -1)(| % |2 -1)E*(x, t%) - бигармоническая по x, % е S . Поэтому функция Q( (x, %) - бигармоническая. Равенство Q( (x, %) |^еж = 0 выполнено, поскольку

|      - 1 x | % | ² = 1 - 2 x %+ 1 % | ² | x | ² = | x -% | ²

1 x| на  дS,  а значит,  E4 (x, %) = E*(x, %)|^еж. В работе [4] было также установлено, что

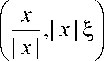
, то A % E * ( x , % ) = - 1 x | ² E *( x , % ) .

A^ E ₄ ( x , % ) = - E ( x , % ), а поскольку E * ( x , % ) = E₄

Воспользуемся двумя следующими равенствами. Пусть v ( % ) - гармоническая функция по

%е S , тогда

А% (| % |2 v(%)) = 2nv(%) + 4Л%v(%) = 2(2Л% + n)v(%) ,(7)

(2Л£ + n) f1 v (t %) tn/2-1 dt = 2 v (%).(8)

%Jo

Равенство (7) легко проверяется, а равенство (8) следует из равенств

2Л, Г v(t%)tn/2-1 dt = 2 Г't(v(t%))'ttn/2-1 dt = 2v(t%)tn/2 |1 -n f1 v(t%)tn/2-1 dt = 2v(%) - n ['v(t%)tn/2-1 dt. J0                         J0                                            '      J0J0

Следовательно, учитывая (7), (8) и гармоничность E * ( x , t % ) по % е S , получим

A^ | % |4  1 j1E* (x, t%)tn/2-1 dt = 1 (2Л + n)£ E* (x, t%)tn/2-1 dt = E* (x, %), откуда следует, что

Д ^% ( x , Q ) = - E ( x , Q ) + 1 x | ² EXx, Q ) - (| x | ² - 1) E\x , Q ) = - G 2 ( x , Q ) .

Поскольку G ₂ ( x , Q ) 1^ = 0 0 , то Д^ n ( ( x , Q ) |^_€ = 0 0 . Утверждение 1) доказано.

• 2)    Из равенства (5) видно, что функция n ( ( x , Q ) имеет сингулярность, содержащуюся в E ₄ ( x , Q ). Рассмотрим бигармоническую функцию H ( x ) = g n ( x, Q ) - E ₄ ( x , Q ) . По теореме 1 из [7] для произвольной функции u g C ⁴( S ) n C ³( S ) справедливо равенство

Г г / пл2         f fr/ _^ч5Д u  5 E ₄( x ,Q) .    .      du^  дД E ( x ,Q)    V

I E ₄( x , Q ) Д u ( Q ) d Q = I    E ₄( x , Q )---⁴----- Д u +Д E ₄( x , Q )--- u ( Q ) \ds. + to„ u ( x ) ,

Js 4                  JdsV 4      Sv      Sv            4      Sv      Sv        J Q n которое основывается на формуле Гаусса–Остроградского. Поэтому если в это равенство вместо E^ (x, Q) подставить бигармоническую функцию H(x), то получим аналогичное равенство, но без члена ©й u (x). Если теперь сложить эти равенства, то будем иметь

Ц4 ⁿ ( x , Q ) Д ² u ( Q ) d Q = [

J S                           J g S

V

- n, „_ч6Д и  dQ n ( x , Q )        -n_z dU^u   дД-Q n ( x , Q )    V

£4(x,Q)-z---к—- Ди + ДЙ| (x,Q) “---г----u(Q) dsQ + Йnu(x), dv     dv                dv     dv       J

откуда, с учетом равенств g n ( x , Q ) | q_{g5 S} = Д ^ Q^ ( x , Q ) | q_g5 S = 0, сразу следует (6). Теорема доказана.

Таким образом, функция n ( ( x , Q ) является функцией Грина задачи Навье.

Пусть { H ^{( 1} ) ( x ): i = 1,..., h_k , k g N_o } - полная система однородных степени k g N_o ортогональных на   d S  гармонических полиномов (см., например, [11]), нормированных так, что

Г             7               7    2 k + n - 2 [ k + n ^- 3 Л              _{/ ;}

I ( H () ( Q )) ds. = to , где h_k =--------- при n >  2 ( h_k = 2 при n = 2) - размерность

J as   k          Q n'        k      n - 2 I n - 3 J                  k базиса однородных гармонических многочленов степени k . hk

4.1] для

Рассмотрим следующий полином T~l_k ( x , Q ) = ^ H ( i ) ( x ) H( i ) ( Q ). В [4, теорема i = 1

| Q | < | x | < 1 были получены следующие представления элементарных решений:

”

E 4 ( x , Q ) = 1 X

² k = 0

^{1 x 1}

I-(

■^{(2 k + n - 2)} f      | x | ²            | Q |

—

2 к + n - 2  2 k + n - 4  2 k + n

Н k ( x , Q ), ( n >  4),

® I   i-(2 k + n - 2)                                 ®         i

E ( x , Q ) = X У-----74( x , Q ), E *( x , Q ) = X------- 4( x , Q ), ( n >  2),

_k_Q 2 k + n - 2                     _k_Q 2 k + n - 2

а в случае | x | < | Q | < 1 переменные x и Q надо поменять местами. Записанные выше ряды сходятся равномерно по x и Q при | x | < a < | Q |. Заметим, что в представлении (10) функции E ( x , Q )

суммируются гармонические полиномы H(i)(Q), умноженные на преобразование Кельвина этих же полиномов K(H(i)(x)) =| x |-(2k+n-2) H(1)(x) от переменной x с коэффициентами 1/(2k + n - 2).

Лемма 1. Имеет место равенство

• 1г                            f 0,       k ^ m ,

• —    L^ k ⁽ x ’ У ) ^Hm ⁽ У ’^Q) ds y 4^/ П К . to _n ^{d SS                       y}   [ n_k ( x , Q ),   k = m .

Доказательство. Действительно, hkh

— L Л (x, У ) ^ (У, Q) dsy =—J У Hki)(x) Hki)(y )£ Hmmj)(y) Hmmj )(Q) dSy = ton JS                         ton dSS^

I                         ⁰,

J h k

X H ki ) ( x ) H ki ) ( Q ) = h ( x , Q ),

< i = 1

k ^ m, k = m.

hkh

XX H«( x) HmkQ)—f H«( y) Hmmj)(y )dsy = M У             ton JSS поскольку по ортогональности на dS системы полиномов {H(i) (x): i = 1,..., hk, k g No} имеем

Математика

— J H?\У ) H mj ) ( У )dS y = I ¹

k = m, i = j , иначе.

® n ^{d SS}                         [ 0,

Лемма доказана.

Приведенные представления (9) и (10) полезны при нахождении интегралов вида

Qn (x, %)| % |m H(%) d% с ядром из функции Q( (х, %), где H(%) — некоторый гармонический по-S лином. Докажем следующее утверждение.

Теорема 2. При n >  4 и | % | ^ | х | < 1 справедливо равенство

— f G2 (х, У)G2 (У, $ dy = E4 (х, %) - E4* (х, Q - i^L-1 LIL! f1 e* (х, tQtn/2-1 dt,(11)

ton^S                                                       22 т. е. Gn (х, %) = Q( (х, %) при указанных выше условиях.

Поскольку

£ G2 (х, y )G2 (У, %) dy = £ ( E (х, У) - E * (х, y))( E (y, %) - E * (y, %) ) dy,(12)

то доказательство теоремы можно разбить на 3 леммы.

Лемма 2. При n >  4 и | % | < | х | < 1 верно равенство

--£ ^{E (} х , У ) ^{E (} У , % ) dy = E 4 ⁽ х , % ) ^- ^              2 ^пк ( х , % ) ,

^Ю n ^J                                к = 0 ⁽ k ⁴⁾⁽ k ²⁾

где для удобства введено обозначение k = 2 k + n .

Доказательство. Поскольку при х ^ % интеграл из леммы имеет интегрируемые особенности при y = % , y = х , то запишем интеграл в виде

<^ |   | х |    1 А

| % |      | ^х |

—£ E ( х , y ) E ( y , % ) dy = — f + J + f

^(,)n                                    ® ⁿ I 0 | % | | х | J

Р n ^{- 1 d} pf , , ^{E (} х ’ P У ) ^{E (} P У ’ % ) ^ds y .

^JI У ^| = ¹

Вычислим полученные интегралы.

• 1)    Пусть | y | < | % | < | х | < 1. Воспользуемся представлением (10), леммой 1 и обозначением k = 2 k + n

| % |

— f P ^{n - 1 d} p[ . , ^{E (} х , Р У ) ^{E (} P У , %) dS y =

® n ^J₀          ^{J| y} ^‘

^| % ^|             1 с ” I r I^{- ( k - 2)}                  “ I P I^{- ( m - 2)}

= [р ^{n - 1} d Р — f У       ^ ( х , Р У ) X ^L %—^ ^ m ( Р У , % ) ds y =

0        ® n^{j|y = 1} k = 0 k - ²          ~0 m - ²

_ у у | х Г ^{( k - 2)} | % | ^{- ( m - 2)} %

J k=0 m=0  k 2   m 2 0

-( I ,P ^{2 ( х} , У ) ^Hm ⁽ У , % ) ds y =

°_n   У ^| = ¹

к = 0

_| - ( k - 2)_| % _| - ( k - 2)

( k - 2) ²

| % |                      ^

Ух ( х , % ) J p ^k - d p = X

к = 0

х | " ’k^-2) | %      ₍V^

( k - 2) 2 k       ’ ^х ’ % ) •

2) Пусть | % | < | y | < | х | < 1. Аналогично предыдущему найдем ^{| х |}

— ( Р n ^{- 1 d} p[ . , ^{E (} х , Р У ) ^{E (} P У , % ) dS y = ® n

| % |

XX k=0 m=0

Р 4 J ЦР? (-* У ) X    m    ( Р y , % > d y =

«,л ^{| = 1} k = 0 k ^{- 2}          ~0   m - ²

I r I - ( k - 2)¹ х      n- ( m - 2)        1 e

/рn-1       dР-  . /kH*(х,У)Hm(У,%)dsy = k - 2 J     m - 2   ®n J|yH

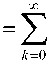
( k - 2) ²

I x I                 x

^k(x, ^) fp d P = X

KI            ^k = ⁰

| x | — ^{( k - 2)} (| x I ² - 1 i I ² )

2( k - 2) ²

4 ( x , i)

3) Пусть | i | <  | x | <  | y | <  1. Аналогично предыдущему найдем

—fp n ¹ d pf ^{E (} x ’ P y ) ^{E (} P y ,ⁱ⁾ dS y = fp n ¹ d P “f I _lX ^{lp y} Ц^_^⁽ x ’ P y ) £ ® n x 1        y = 1                        x       ® n^{J 1}   k = 0 ^{k - 2}

| p y r ^{(m- 2)}

m - 2

К m ⁽ Р У , ^{i )} dS y =

x x ¹

=££ fp k=0 m=0  | x |

n- ( k - 2) A- ( m - 2) n - 1 ^{p       p}

к - 2 m - 2

d Р “I i ,P² k^{Hk (} x ’ y ) ^m ⁽ y ’ ^{i )} dsy = Ю_п ^J| y |=1

k = 0

1 n- 2( k - 2) + k - 1          x     . I   ,-( k - 4)x

4 ^p—г d p = У    —Ute x . ә.

J   ( k - 2) 2 ^{P  £} - ( k - 4)( k - 2) 2 ^k "

^| x ^|

С учетом сделанных вычислений найдем

'

— J E ⁽ x , y ) E ⁽ y , ^{i )} dy = ^ ® n ^Ss                  tt I

x

l x - k z!l f. ( k - 2) ² I

| i | ² k

| x | ² - 1 І |² ,    | x | ²

—

( k - 4)

( k - 4)( k - 2) ²

h k ( x ,0. (13)

Поскольку

+txM+f 1 -1 ЪхР f 1

k        2       k - 4      к k 2 J     к 2

то с учетом (9) получим

k - 2  ,   ,2

k - 4 )  2( k - 4)

-        |^  ,

| x | ^{- ( k - 2)} f

k = 0

( k - 2) ²

к

litД k

- 1 i | ² ,  | x | ² 1

k - 4 )

1 x

Hk ( x , i ) = - £

² k = 0

I x \

I-I

■^(k - ²⁾ ( | x | ²

( k - 2) _к к - 4

—

12 A

^l|- ^ k ( x , i ) = E 4 ( x , i ) . ^k )

Используя найденное равенство из (13), сразу получаем утверждение леммы.

x

Заметим, что существование гармонической функции £w_t( x , i )/( k - 4)( k - 2) ² из леммы 2

k = 0

было ранее теоретически доказано в [7].

Лемма 3. При n >  2 и | i | < | x | < 1 верно равенство

x

1 ^x

—L E ^{( x} , y ) E ⁽ y ’ ^{i )} dy = E

® n ^Js                 T^

1 | x | ² - 1

k = 0 к

--------------7----

( k - 2) ² k 2( k - 2) k

кk ( x , 0.

Доказательство. Поскольку представление E *( y , i ) из (10) не зависит от взаимного расположения i и y , то

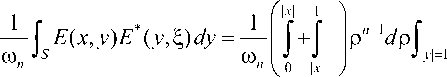
^E ( ^x , P y ) ^E *( p y , ^{i )} ds y .

Тогда будем иметь

1 ^| x                                                               ^| x¹                i             x । |- (k-2)                    x       .

— f P n ^{- 1 d} pf . ^{E (} x , P y ) ^E *⁽ P y , ^{i )} dS y =fp ^{n - 1 d} P—f . У-—— К ⁽ x , P y )£--- ;mk ⁽ P y , ^{i )} dS y =

® n 0        ^Jy = *                        ^J0        ® ,,^Jl k = 0 ^{k - 2}            m = 0 m ^- 2

=££ k=0 m=0

| x | ^{- ( k - 2)} k - 2

|

— fp ^{n - 1} d p —I   p ^{2 k}H_k ( x , y ) К ( y , i) ds y

- 21         m J|y|=1

x

=£ k=0

| x | ^{- ( k - 2)} ( k - 2) ²

w k ( x , rp ^{- 1} d p= £ 0              ^k = ⁰

L x^ ( k - 2) ² k

Д I ҮІ2

У⁽ x ,⁹= £ ГтЬ); У⁽ x , ⁹ k = 0 ^{( k 2) k}

Аналогично получим

1 ^{1                                                              1}               1             x I      |- (k - 2)                   x       1

— (P ^{n - 1 d} pf . , E ( x , P y ) ^E *⁽ P y ,ⁱ⁾ dS y = f P ^{n - 1 d} P—f . .£ ^y о ^k ⁽ x , P y )£----- mk ⁽ P y ,^{i) ds} y =

® nx      ^Jy=1                       j x |        ® n^{Jy 1} £0   ^{k -} 2            m = 0 m ^- 2