Представление решения системы линейных неоднородных двухмерных разностных уравнений дробного порядка a

К настоящему времени рядом авторов изучены различные свойства 2D линейных систем, описываемых разностными уравнениями дробного порядка [1–3] и др.

В предлагаемой работе некоторые идеи работ [4], используются для решения линейных неоднородных разностных уравнений дробного порядка и установлены представления решений в явном виде.

1. Основные понятия [4]

Определение 1. Расширенный ( а^л биномиальный коэффициент I     определя-

I n )

ется следующим образом

( а Л

< ⁿ )

Г ( а + 1 )

Г ( а - n + 1 ) г ( n + 1 ) ,

n >  0

= <  1,                      n = 0

n <  0.

Определение 2. Пусть 0 <  а <  1, дробная

сумма порядка образом:

Л "и ( n ) =

n

= Е j=1

In

-

а определяется следующим

n -1 Е j =0

j + "

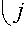
j + " - p

^j        )

u ^{( n -} j ) = )

( j ) ,

а дробный оператор порядка а определяется следующим образом:

n-1 Aau (n ) = E j =0

(J - a

у u ^{( n} - J ) =

E ⁽ n ^- j ^{- a} j =1 1 ^{n -} j

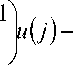
(n

I n

- a

-1

-

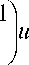
2. Постановка задачи

Рассмотрим систему 2D линейных уравнений дробного порядка a :

A “ z ( t + 1, x + 1 ) = A ( t, x ) z ( t, x ) + B ( t, x ) z ( t + 1, x ) + + C ( t , x ) z ( t , x + 1 ) + f ( t , x ) ,                      (1)

z ( t ₀, x ) = a ( x ), x = x ₀, x ₀ + 1,..., x ₁ ,

z(t, x0 ) = b(t), t = 10,10 + 1,..., 11 , a (x 0 ) = b(t 0) .                                    (2)

Здесь A ( t , x ) , B ( t , x ) , C ( t , x ) – заданные ( n x n ) -мерные дискретные функции, g ( t , x ) - заданная n -мерная дискретная функция, b ( t ) – заданная дискретная векторная функция, а a ( x ) - n -мерная вектор-функция, являющаяся решением линейного разностного уравнения

A ^-a A ^a z ( t + 1, x + 1 ) = A ^{- a} ( a ^{1 -} ^ z ( t + 1, x + 1 ) ) =

A ^{- a} A ^{- M} ( A z ( t + 1, x + 1 )) = A ^{- 1} ( A z ( t + 1, x + 1 )) = tx

= EE ^{( z ( J + 1} s ^{+ 1 )- z ( J} , s )) =

J = 1 0 s = x 0

= z ( t + 1, x + 1 ) - z ( t ₀, x 0 )                       (5)

Принимая во внимание (5) представления (4) можно записать в виде:

z (t,x ) = z (t 0,x 0 )+ EE Ra (t -1 x -1; J, s )A (J, s )z (J, s ) + j=t 0 s=x0

+ZE Ra(t-1 x-1;J’s)B(J’s)z(J’s+1)+ j=t 0 s=x0

⁺ EE R a ⁽ t ^{- 1 x - 1} ; j ’ ^sC ⁽ J ’ ^s ) ^{z (} J ^{+ 1 s ) +}

^J = t 0 ^s = x 0

t - 1 x - 1

⁺ EE R a ⁽ t ^{- 1 x - 1} ; ^j , ^s f ^{( j} , ^s )’

^J = t 0 ^s = x 0

где

	t - J + a -1>	( x - s + a - 1 ^
R a ( t , x : J , s ) =		< x - s      J
	. t - J        J

a ( x + 1 ) = D ( x ) a ( x ) + g ( x ), x e X , a ( x ₀ ) = a ₀.

Требуется найти представление решения системы уравнений дробного порядка (1)– (3) через аналог матрица Римана.

3. Представление решения

Пусть 0 <  a <  1 и ^ = 1 - a , применим

A^- “ обеим сторонам уравнения (1).

A^- “ ( a “ z ( t + 1, x + 1 ) ) =

A^- “ ( A ( t , x ) z ( t , x )) + A^- “ ( B ( t , x ) z ( t + 1, x )) +    (4)

A^- “ ( C ( t , x ) z ( t , x + 1 ) + f ( t , x )) .

Теперь рассмотрим выражение

A ^- A ^a z ( t + 1, x + 1)

Учитывая свойства операторов дробной суммы и дробной разности проведем следующие преобразования:

Используя    замену    переменных j +1 = a , s +1 = в доказывается справедливость следующих тождеств:

t -1 x -1

EE R a^{( t - 1 x - 1}; ^J , ^s ) ^{B ( J} , ^s ) ^{z ( J + 1 s} ) =

J = t 0 ^s = ^x 0

= E E R a ( t - 1. x - 1; J - 1, s ) B ( J - 1, s ) z ( J , s ) =

J = 1 ₀ +1 s = x 0

t -1 x -1

= E E Ra(t -1 x -1;J -1 s)B (J -1 s)z (J,s)+ j = 10 s = x 0

x -1

+ E Ra (t -1, x -1; t -1, s)B(t -1, s)z(t, s )- s=x 0

- E R (t -1, x - 1; 10 -1, s ) B (t0 -1, s )z (t0, s ) = s = x 0 t-1 x-1

EE Ra(t -1 x -1;J -1 s)B (J -1,s)z (J,s)+ j=t0 s=x0

E R (t -1, x -1; 10 -1, s)B (t0 -1, s)z (t0, s), s=x 0

g 2 Ra (t-1, x -1;,, sC (j, s)z (j, s +1)- j=t 0 s=x 0

t -1    I

2 g Ra (t - 1, x - 1 j, s - 1)C(j, s - 0z(j, s) = j=t оs=x 0 +1

t -1

= g Ra (t -1, x -1; j, x - 1)C(j, x - 1)Z(j, x)- j = t о t-1

• ^-    g ^R a ^{( t -} 1, ^{x - 1; j} , ^x 0 ^{- 1 C ( j} , ^x 0 ^- 1 ) ^z ( ^j , ^x 0 ^{) +}

j = t 0

t -1 x -1

+ g 2 R (t, x; j, s - 1)C (j, s -1)z (j, s)= j=10 s=x0

t -1 x -1

-ggR (t, x; j, s - 1)C (j, s -1)z (j, s )- j=10 s = x 0

t -1

• ^-    g ^R a ^{( t - 1}, ^x - ^{1; j} , ^x 0 - ^{1 ) C (} j ’ ^x 0 - ^{1 ) Z (} j ’ ^x 0 ^{) (7)} j = t 0

Принимая во внимание тождества (5)–

• (7) в (4) будем иметь

z ( t , x ) = z ( t 0 , x 0 ) =

= g g R a ⁽ t - 1 x - 1; j , s ⁾ A ⁽ j , s ⁾ z ⁽ j , s ⁾+

.j = t 0 ^s = ^x 0

+ g g R a ( t - 1, x - 1; j - 1, s ) B ( j - 1, s ) z ( j , s ) +

.j = 1 0 s = x 0

g Ra (t - 1, x - 1 t0 - 1, s )B (t0 - 1, s )z (t0, s ) + s = x 0

t - 1 x - 1

+ g g R(t -1, x -1;j, s - i)c(j, s -1)z(j, s)+ j = t 0 s = x 0

g Ra (t - 1,x - 1; j, x0 - 1)C(j,x0 - 1)z (j, x0 ) + j=t 0

t —1 x —1

⁺ gg ^R a ^{( t - 1 x -} 1; ^j ’ ^{s )} f ^{( j} , ^{s )} •            (8)

J = t 0 ^s = ^x 0

Теперь      предположим,      что

R _a ( t - 1, x - 1; j , s ) является решением следующей задачи:

R a ( t - 1, x - 1; j , s ) A ( j , s ) =

= -Ra (t - 1,x -1; j - 1,s)B(j - 1,s)-

• - R _a ( t - 1, x - 1; j , s - 1 ) C ( j , s - 1 ) ,

j = t - 1,..., 1 0 , s = x - 1,..., x 0 , R _a ( t , x ; t - 1, x - 1 ) = E .

Тогда из тождества (8) следует что, z (t, x )= z (t 0, x 0 ) +

+ g Ra (t - 1 x - 1; j,x0 - 1) C (j,x0 - 1)z ( j ,x0 ) + j=t 0

+ g Ra (t - 1, x - 1; 10 - 1, s ) B (t 0 - 1, s )z (t 0, s ) + s = x 0

t - 1 x - 1

⁺ gg ^R a ^{( t - 1 x - 1 T} ,^{s )} f ⁽ j , ^{s )} .

j = t ₀ s = x ₀

Принимая во внимание (2) представления (8) можно записать в виде:

z (t, x ) = a (x0)+

( - 1

+ g Ra (t-1, x-1; j, x0 -1) C (j, x0 - Ф (j) + j=t 0

+ g Ra (t -1, x -1; 10 -1, s) B (t 0 -1, s) a (s) + s=x 0

t - 1 x - 1

+ gg Ra (t-1, x-1T,s)f(J,s) .                      (9)

j = t ₀ s = x ₀

Известно, что a ( x ) решения линейных неоднородных уравнений в виде (3) и это решение определяется в следующем виде [5–6]:

x - 1

a ( x ) =Ф ( x , x 0 - 1 ) a ( x 0 ) + g o ( x , s ) g ( s ). (10)

s = ^x 0

Здесь матричная функция   ф ( x , s )

является решением следующей задачи:

ф ( x , s - 1 ) = ф ( x , s ) D ( s ), Ф ( x , x - 1 ) = E .

E - n x n -мерная единичная матрица.

Подставляя (10) в (9) будем иметь:

z (t, x ) = a (x0) + t-1

+ g Ra (t - 1, x - 1; j, x0 - 0 C(j, x0 - Ф(j) + j = t 0

x - 1

+ g Ra(t -1,x -1;t0 -1,s)B(t0 -1,s)x s = x 0

s- ф(s,x0 - l)a(x0 )+ 2ф(s,T)g(T)

t = t 0

+

t - 1 x - 1

+ g g Ra (t - 1 x - 1;T,s)f(j,s)- j=t0 s=x0

Отсюда, используя дискретный аналог двумерный леммы Фубини [7], имеем

z (t, x ) = a (x 0)+ t-i

+ E Ra (t -1’ x -1; j ’ x0 - 0C(j ’ x0 -1)b ( j ) + j=t 0

x - 1

+ £ R _a ( t - 1, x - 1; 1 0 - 1, 5 ) B ( 1 0 - 1, 5 ) ф ( 5 , x 0 - 1 ) a ( x ₀ ) +

⁵ = x 0

x - 1 x - 1

+ EE Ra (t -1, x -1;t0 -1 T)B(t0 -1TM,5)g(5) +

⁵ = x 0 T = ⁵

t - 1 x - 1

+ EE R a ⁽ t ^{- 1} x ^{- 1}; j ^{, 5} ) f ⁽ j ^{, 5} )                     ⁽¹¹⁾

j = t 0 ⁵ = x 0

Таким образом, доказано следующее:

Теорема. Решение z ( t , x ) системы линейных 2D-разностных уравнений дробного порядка (1)–(3) допускает представление в виде (11).