Предварительная оценка эффективности применения миграции перед суммированием данных малоглубиннои сейсморазведки при поисках локальных неоднородностей: анализ данных моделирования

В последнее время широкое применение получили методы миграции сейсмических данных, которые позволяют получать более точное изображение геологического разреза, чем применявшийся ранее метод общей глубинной точки (МОГТ) (Yilmaz, 1979; Claerbout, 1985; Козлов, 1986). На ранних стадиях развития метода миграция использовалась в основном для коррекции положения наклонных отражающих границ. Сейчас процедуры миграции входят в стандартный граф обработки ведущих компаний при поисках месторождений нефти и газа. В настоящее время разработано большое количество программ и алгоритмов проведения миграционных преобразований (Gray et al, 2001). Миграция после суммирования используется в основном для вос- становления корректного положения наклонных границ, миграция до суммирования дает возможность получить более точное изображение сложнопостроенных сред (Yilmaz et al., 1980; Audebert et al, 1997). При детальном исследовании сложных геологических объектов наиболее эффективными оказались методы глубинной миграции (Gray et al, 2001).

В связи со значительной изменчивостью скоростных характеристик верхней части разреза использование метода МОГТ имеет ряд свойственных ему ограничений, особенно при изучении локальных неоднородностей. Использование методов миграции может существенно повысить качество восстановления сейсмического изображения таких сложных геологических структур, как карстовые образования разных форм. Опыт ранее прове-

денных исследований показал эффективность программ миграции до суммирования при обработке данных малоглубинной сейсморазведки (Bradford et al., 2002; Bradford et al., 2006; Basak et al., 2008). При использовании новых методов обработки или обработки данных для новых объектов изучения целесообразно проводить предварительную оценку алгоритмов и их параметров на примере модельных данных (Редекоп и др., 2008). Для оценки возможностей алгоритмов миграции сейсмических данных до суммирования при локации подземных полостей нами были проведены предварительные исследования на примере данных моделирования полного волнового поля.

Методика, параметры и обсуждение результатов вычислительного эксперимента

На данном этапе исследований использовались возможности известного программного пакета Seismic Unix (SU), разработанного в Горной школе Колорадо (Stockwell, 2008). Он включает в себя широкий спектр программ моделирования и обработки сейсмических данных для работы в среде Unix/Linux. В связи с большим объемом вычислений моделирование сейсмических данных и их обработка были проведены на базе суперкомпьютерного комплекса Научно-образовательного центра «Параллельные и распределенные вычисления» ПГНИУ.

Для вычислений была использована упрощенная модель подземной полости, заполненной материалом разрушения, и соответствующего распределения скоростей продольных, поперечных волн и плотностей (рис. 1). Параметры разреза даны в таблице.

Параметры структурных элементов разреза

Моделирование сейсмических данных проводилось полноволновым конечноразностным методом (Operto et al., 2007) с помощью программы SUEA2DF ((an)-elastic anisotropic 2D finite difference forward modeling)).

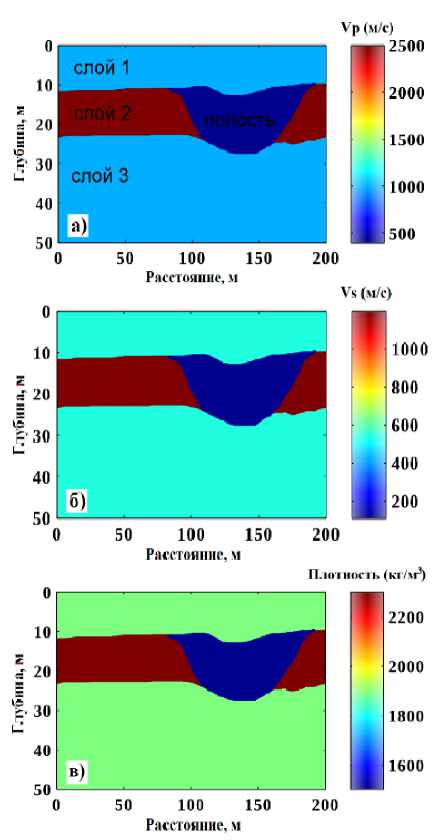
Рис. 1. Модель распределения физических параметров разреза: а – скорости продольных волн; б – скорости поперечных волн; в – плотность

Модель разреза размером 200х50 м была использована для расчета 101 сейсмограммы при шаге пунктов возбуждения 2 м. Моделируемая система наблюдений – центральная с раскрытием и закрытием. Длина записи – 100 мс. Средняя частота – 200 Гц. Интервал дискретизации – 0,02 мс. Форма сигнала – производная функции Гаусса.

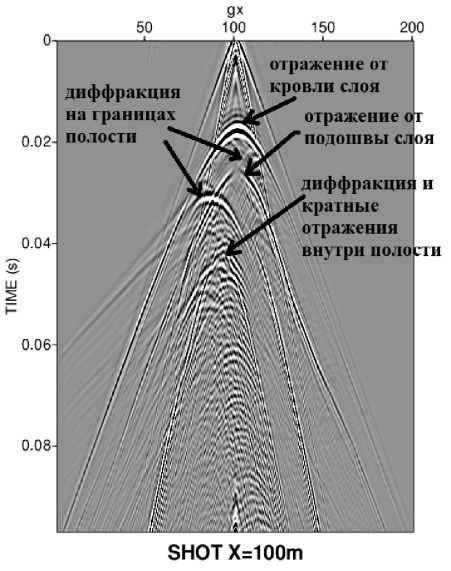
Рис. 2. Модель сейсмограммы, полученной при Х ПВ =100 м

В результате полноволнового моделирования (Levander, 1988) рассчитываются все характеристики волнового поля: пространственно-временное изменение сигнала, его фаза, амплитуда, форма для всех типов волн (продольные, поперечные, поверхностные, обменные, кратные и т.д.). В данном эксперименте модельные данные рассчитывались без учета затухания и анизотропии. Пример модели сейсмограммы ОПВ, полученной при Х ПВ =100 м, показан на рис. 2.

Рассчитанные по сейсмическому профилю модельные данные были преобразованы в изображение среды с использованием программы SUMIGPRESP, реализующей алгоритм миграции общего пункта возбуждения (ОПВ) методом Фурье с разделенным шагом и деконволюцией (splitstep Fourier shot-record migration with deconvolution imaging) (Hardin et al., 1973; Lee et al., 1991; Bogomolov et al., 2006). Преимуществом данного метода является то, что обработка в частотной области позволяет значительно сократить размер используемой компьютерной памяти и соответственно увеличить скорость выполнения задания.

В результате миграции получен глубинный разрез, где уверенно локализуется область расположения полости (рис. 3). С высокой степенью достоверности восстановлены верхняя и боковые границы объекта. Нижняя граница выделяется недостаточно точно, что, возможно, связано с влиянием помех, представленных многократными отражениями внутри полости. В ходе работ была отмечена существенная зависимость качества получаемых изображений от точности задания скоростной модели и параметров фильтра, используемого для уменьшения влияния хвостов функции Грина.

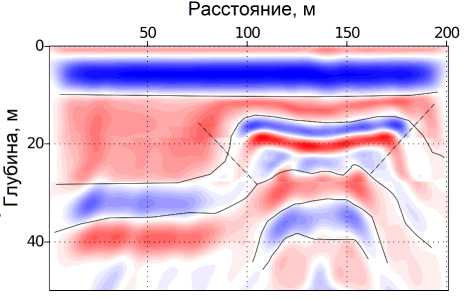
Рис. 3. Изображение среды, полученное с помощью программы SUMIGPRESP. Границы полости отмечены пунктирными линиями

Заключение

Данные, полученные в результате экспериментальных работ, подтвердили эффективность использования методов миграции до суммирования для изучения малоглубинных разрезов со сложным строением. Для повышения качества получаемых с помощью данного алгоритма сейсмических изображений рекомендуется особое внимание уделять точности задания скоростной модели среды и параметров фильтра.