Преемственность содержания в изучении теории вероятности в школе и вузе

Изучение теории вероятности и статистики в школе имеет множество перспектив в различных областях жизни, включая науку, бизнес, экономику, финансы, проведение исследований и принятие обоснованных решений. Она также является одной из важнейших наук технологического развития, без которой невозможно проектирование транспортных технологий и разного вида механизмов. Знание статистики и вероятности необходимо для проведения экспериментов и анализа большого количества данных в различных областях науки.

При построении плана преподавания теории вероятности на школьном уровне, в учебниках учитывается возрастной контингент учащихся и уровень их математической подготовки. Подача теории проводится на элементарном, для школьников юного возраста уровне, а также менее строго.

Первое знакомство со статистическими понятиями у учеников начинается с чтений таблиц, диаграмм (столбчатых и линейных) и деревьев вероятности, их составлением и построением. Вводятся понятия случайных, достоверных, невозможных, равновероятных событий [1].

Потом изучаются задачи с разными видами вероятности. Например:

Вероятность поломки (выхода из строя) в течение дня из трех работающих кранов равна соответственно Р 1 =0,05 Р 2 =0,2 Р₃=0,35. какова вероятность того, что в течение рабочего дня:

• а)    все краны выйдут из строя

• б)    ни один не выйдет из строя

• в)    хотя бы один выйдет из строя

• г)    точно один выйдет из строя

Решение:

• а)    P=0.05^0.2^0.35=0.0035

• б)    Р=1-0,05^0,2-0,35=0,9965

• в)    Р=0,05 • (1-0,2) • (1-0,35)+(1-0,05)

0,2 • (1-0,35)+(1-0,05) • (1-0,2) • 0,35+0,05 • 0,2 • (1-0,35)+0,05 • (1-0,2) • 0,35+(1-0,05) • 0,2 • 0,35+0,05 • 0,2 • 0,35=0,506

• г)    Р=0,05^  (1-0,2)  •  (1-0,35)+(1-0,05)

0,2 •    (1-0,35)+(1-0,05)    •    (1-0,2)

0,35=0,4155

На уровне вузовского изучения теория вероятности может использоваться для определения надежности механизмов. Рассмотрим пример нахождения полной веро- ятности безотказной работы механизма поворота крана «Альбатрос», имеющего два двигателя и, соответственно, два привода открытой передачи.

Работа двигателей неразрывно связана с работой механизма поворота стрелы крана, при этом при отказе одного из двигателей механизм поворота всё равно может работать, но с несколько меньшей эффективностью.

При работе обоих двигателей механизм поворота отказывает с вероятностью q12 =0,95(отказ может быть вызван дефектами в работе открытой передачи), при работе только одного двигателя механизм поворота отказывает с вероятностью д1=0,2,работе второго двигателя с вероят- ностью-д2 =0,25. Надёжность работы первого двигателя р1=0,8, второго р2=0,75. Все элементы могут выйти из строя независимо друг от друга.

Найти полную надежность (вероятность безотказной работы) механизма поворота.

• Н₁₂- работают оба двигателя

Н 1 - работает только первый двигатель (второй вышел из строя)

Н2- работает только второй двигатель (первый вышел из строя)

Н0- оба двигателя вышли из строя

А- безотказная работа привода механизма поворота

Решение:

P(A) = Р(Н 1 ) • Р(Н 2 ) • P GA) + ^р(Н 1 ) • (1 - ’№)) ■(’(A PW        ₍₁₎

■(1-р(Н1^р(А

P(A) = 0,8 • 0,75(1 - 0,95) + 0,8 • 0,25(1 - 0,2) + 0,2 • 0,75(1 - 0,25) = 0,8 • 0,75 • 0,05 • 0,8 • 0,25 • 0,8 + 0,2 • 0,75 • 0,75 = 0,3025

Таким образом полная вероятность безотказной работы механизма поворота крана «Альбатрос» при данных условиях равна 0,3.

Вычисленная вероятность является очень малой, поэтому для увеличения надёжности крановой конструкции необходимо повышать работу двигателя, например за счёт совершенствования конструктивной схемы (изменение места расположения муфты, изменение марки двигателя, применение материалов для изготовления двигателя с более высокими прочностными свойствами) [2].

В специальных дисциплинах, в частности теории надежности, используются знания полученные при изучении дисциплины математика раздела теории вероятности и математической статистики.

Для анализа влияния наработки на изменение механических характеристик материала были получены образцы после испытаний в Институте машиностроения и собраны статистические данные предела прочности опорного барабана плавкрана КПЛ-5-30.

• 1    партия: 294,98; 304,78; 300,86; 308,70; 291,062

• 2    партия: 271,74; 265,85;275,66; 255,06; 262,90

Полученные данные были расположены в вариационный ряд. Далее по ним было вычислено среднее значение и среднее квадратическое отклонение для оценки влияния наработки путем сравнения значений двух партий образцов.

_ _ Z " ₌₁ ^                ^(Г) = 300.08

^Х = П                   ^(2 ' ) = 266.24

(

s =

J

£(t i -y n — 1

S(1) = 7.15

S(2) = 7.98

(

Также существует способ программного гВ программе Excel, была построена

Исследование гипотезы о принадлежности двух партий образцов к одной генеральной совокупности осуществлялось при помощи критерия Граббса [4].

* n	1 партия		2 партия			(4)
	■ X	v 1 =	1.2	v 1 = 1.18
V1       s X-	* 1	v 2 =	1.26		V 2 = 1.4	(5)
v? = —— 2      s Сравнение a = 0,05	для	1.2 ≤ 1.26 1.26 ≤ 1.896		1.18 ≤ 1.869 1.4 ≤ 1.869

Далее была произведена проверка соответствий результатов испытаний нормальному закону распределения.

ПО2

n

= 5-+VW*) - wo)]2

2n  Z—1

1=1

1 партия no² = 0.4201

0.4201 ≤ 0.4614

2 партия no² = 0.38

0.38 ≤ 0.4614

По критерию Фишера мы проанализировали можно ли объединить две партии в одну генеральную совокупность. Точный критерий Фишера в основном применяется для сравнения малых выборок. Этому есть две весомые причины. Во-первых, вычисления критерия довольно громоздки и могут занимать много времени или требовать мощных вычислительных ресурсов. Во-вторых, критерий довольно точен, что позволяет его использовать в исследованиях с небольшим числом наблюдений [3].

S2

F = -max = 1,24 c 2          , min

1.24 ≤ 6.34

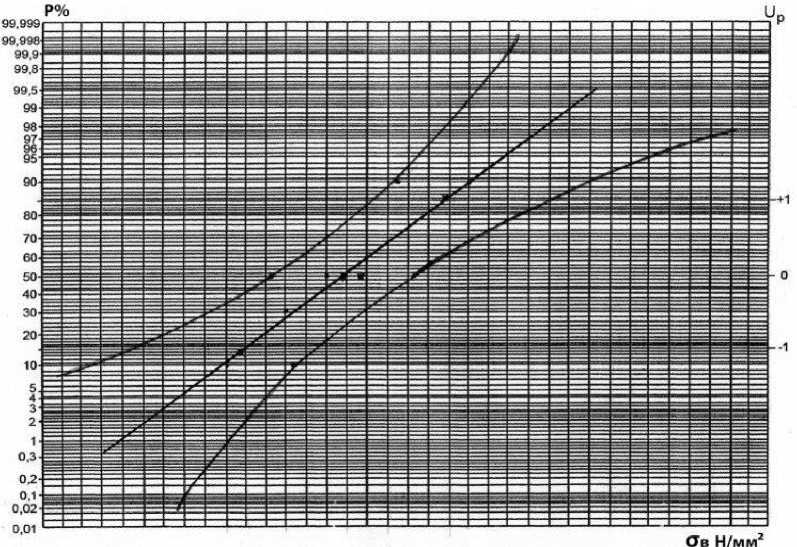
Рис. 1. Вероятностная бумага

Полученные в результате вычислений значения были отмечены на вероятностной бумаге, которая представляет из себя особый тип миллиметровой бумаги, используемый для визуального представления данных, следующих нормальному распределению [5]. По оси Y отмечена вероятность отказа в процентах, по оси X предел прочности материала. При помощи критерия Стьюдента был построен доверительный интервал. Для подъёмно-транспортной техники вероятность отказа выбирается 0,05 (например, для авиации 0,01).

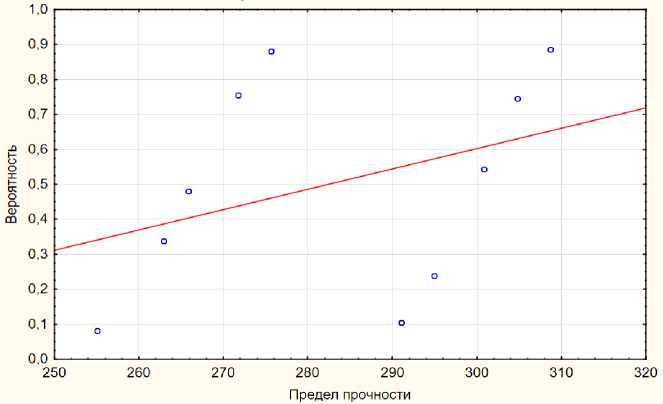
Задачу по построению нормального закона распределения также можно решить, используя современные вычислительные программы. В Excel нами были построены графики для двух партий, в программе Sta-tistica получен графический результат для объединённой выборки.

В зависимости от заданной вероятности отказа на графике можно оценить значение предела прочности для данного материала, что может свидетельствовать о состоянии металлоконструкции крана и служить вспомогательным параметром при опреде- лении ресурса крана.

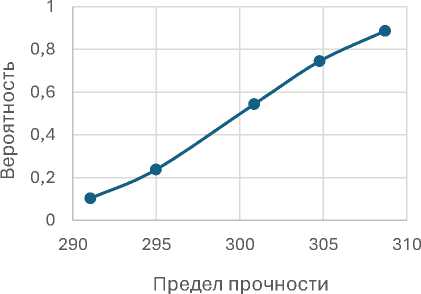
Рис. 2. Нормальный закон распределния для первой партии

0,8

0,6

0,4

0,2

255  260  265  270  275  280

Предел прочности

Рис. 3. Нормальный закон распределния для второй партии