Преобразование Абеля для расчета градиентных оптических элементов со сферически-симметричным распределением показателя преломления

В предыдущей работе авторов [1] в рамках геометрической оптики с помощью пары (прямого и обратного) интегральных преобразований Абеля получены и решены интегральные уравнения для расчета показателя преломления известных градиентных оптических элементов со сферической симметрией (обобщенной линзы Лунеберга [2], для которой интегральные уравнения были ранее получены Морганом [3] и Флетчером [4]; обычной линзы Лунеберга) и цилиндрической симметрией (линзы Микаэляна [5] и аксикона [6]).

В данной работе аналогичным образом с помощью преобразования Абеля получены и решены интегральные уравнения для других известных сфе-рически-симметричных градиентных оптических элементов (линзы Максвелла «рыбий глаз» [7] и линзы-зеркала Итона-Липмана [8]). Кроме того, в работе получено и решено интегральное уравнение для сферически-симметричного градиентного оптического элемента, фокусирующего плоский пучок лучей в радиальную область с заданным распределением интенсивности (распределением плотности лучей), расположенную в плоскости за элементом, перпендикулярной оси падающего пучка. Аналогичная задача, но для расчета градиентного сфери-чески-симметричного оптического элемента, фокусирующего излучение, исходящее из точечного источника лучей в радиальную область, была рассмотрена Флоресом [9].

• 1.    Решение интегрального уравнения Абеля для линзы Максвелла «рыбий глаз»

В [10] в качестве примера «абсолютного прибора», который все лучи, исходящие из произвольной точки сферически-симметричной градиентной среды, собирает также в некоторую точку, лежащую на прямой, соединяющей точки источника и центра симметрии среды, рассмотрен «рыбий глаз» Максвелла.

Получим интегральное уравнение Абеля для такой среды и найдем его решение с помощью формулы обращения. На рис.1 показан ход произвольного луча из семейства лучей, которые исходят из точки на расстоянии а от центра среды с показате лем преломления n=n(r) и сходятся в точке, лежащей на линии, соединяющей точки источника и центра сферы и отстоящей от центра на расстояние b.

Рис. 1. Ход лучей в среде «рыбий глаз»

Общее уравнение для участка луча в сфериче-ски-симметричной среде известно [11]:

02 -0, _ 2 dr h      r, r^n2(r)r2 -h2

где: h _ n ( r * ) r *

*

- постоянная луча, r - радиус, при котором траектория имеет касательную, перпендикулярную этому радиусу, r, r2, 0,, 02 - начальные и конечные радиусы и углы, которые образуют радиусы с осью x, для участка траектории луча.

Для линзы «рыбий глаз» из геометрических соображений (см. рис. 1) уравнение (1) будет иметь вид:

a     dr     +b     dr     _ n r• rVn2 r2 - h2 r' r^n2 r2 — h2 h

Уравнение (2) получено при условии, что все лучи начинаются на оси x в точке a и все они сходятся, также на оси x , в точке b , поэтому угол 0 , - 0 ₂ _ л .

Решим уравнение (2) с помощью пары преобразований Абеля, которые запишем в виде [1]:

^r 0

F ( r ) _ 2 J

r f (x) xdx

/""2      2"

V x - r

f ⁽ x ) = ^-

п

dF ( r )

r —.

Г d r

J . ГУ

d r

F ( r o )

x

x2

В уравнении (10) последнее равенство получено с помощью интеграла (9) и другого табличного интеграла [12]:

Разобьем уравнение (2) на два уравнения с помощью неизвестной функции f(h) :

a J-7 r r Vi b J-7 r • r Vi

x J -rd x= = In 2      2 a \x - a	.     / 2         2 x + V x - a	.                   (11)
	a

' n 2 r 2 - h2	= f ( h ),	(5)
d r	= п- f ( h ). h	(6)
' n2 r2 - h2

Из уравнения (10) в исходных обозначениях получим:

2ln r - ln a - In b = - 2ln

h ■ C h ²  i^v

p

A

C помощью замены переменных: n ( r ) r = p , r = m ( p ), F (p) = In r = In m (p), n ( a ) a = h_a , n ( b ) b = h b , преобразуем уравнение (5) к уравнению (4):

или:

r

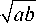
n (r) r n (a) a + 7 n 2( a) a2 - n 2( r) r2

п

_h dp h_a [ dp

J О 23

F ( h a )

,h h

Из уравнения (13) нетрудно получить явный вид зависимости показателя преломления линзы «рыбий глаз»:

п

f ( h )

F ( h a )

^

n ( r ) =

= f ( h ) .

² ^Ть” ^{( a} )

А 2

r I

T ab J

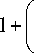
Левая часть уравнения (7) по виду совпадает с правой частью уравнения (4), поэтому для нахождения функции F ( p ) можно воспользоваться уравнением обращения (3). Получим:

или:

, .      ” (0)

^{n ( r} ) = —2ГГЗ , 1 + f r ¹

IS J

a

F ( p ) = 2 J

p

f ( h ) hdh

7 '

2 h r f ( h ) h dh - V h ² -p²

2 F ( h a ) h r п J ^p

h d h

J ( h a - h ² )( h ² -p ² )

2 ² f ( h ) h d h ^{п J} 7 h ² -p ²

+ F ( h a ).

где n (0) = 27 ( a/b ) ■ n ( a ) - показатель преломления в центре симметрии среды при r = 0 , S = T ab - радиус, на котором показатель преломления уменьшается в два раза по сравнению со значением в центре n(0) .

Заметим, что если разбить уравнение (2) вместо уравнений (5) и (6) на два других уравнения:

Последнее равенство в уравнении (8) получено с помощью табличного интеграла [12]:

b

J

* r

dr r^n2 r2 - h2

= f ( h ),

y

J

x

d t

л)(t- x)(У - t)

= п.

dr r^n2 r2 - h2

п- f ( h ), h

Далее подставим в интеграл уравнения (8) функцию f(h) из уравнения (6), получим ( b >  a ):

то вместо уравнения (14) получили бы уравнение вида:

2} h d h

^{F (p)- F ( h} - ) = ^-7 h

-p ²

п

h

' ^ dp b d³ p 7^p2 - hh

h r    d h    ₊ 1 b- d F ( p' )d p' ^pr          d h²

J hlr ^ п‘'    dp'   Ц h2 -p2 )(p'2 - h2)

= - 2ln

'ha + 7ha2 -p2

p

+ F ( h b )

- F ( p ) .

или:

^{n ( r} ) =

2 Vnn ( b ) a

A 2

r I

T ab J

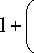
, x     n (0)

n ^{( r} ) = —^2^.

1 + f r1 IS J

Из уравнений (14) и (18) следует, что:

bn ( b ) = an ( a ).                                 (20)

По закону Бугера [10] для любого луча в сфе-рически-симметричной градиентной среде можно записать, что:

h = n ( r ) r sin v _r = n ( a ) a sin V _a =

= n ( b ) b sin v b = n ( r *) r * = const .

инвариант луча, ψ – угол между направлением луча и радиусом до центра линзы.

Уравнение (23) можно решить с помощью пары преобразований Абеля (3) и (4). Для этого введем обозначение:

Этот закон является обобщением закона преломления Снелиуса, углы v _r , V _a , V _ь равны углам, образованным радиус-вектором и касательной в точках r, a и b соответственно.

Сравнивая (20) и (21), можно сделать вывод, что v _a = V _ь . Это означает, что все лучи, исходящие из точки a и входящие в точку b являются дугами окружностей, центры которых лежат на прямой, перпендикулярной отрезку [a, b] и проходящей через середину этого отрезка.

F ( p ) = In r , n ( r ) r = p ,                       (24)

тогда вместо уравнения (23) запишем:

d F ( P )

_ ¹ f d P ^{n J} Tp²"

d p

^^^^^^B

h ²

= f ( h ),

где:

f ( h ) = —

л

л - arcsin h h

2. Расчет градиентной линзы Итона-Липмана

В [8] приведен показатель преломления градиентной линзы Итона-Липмана, которая как сфериче-ски-симметричное зеркало любой луч, падающий на эту линзу, отражает назад. Показатель преломления такой линзы-зеркала имеет вид:

Обращая уравнение (25) с помощью преобразования Абеля (3), получим:

F ( P ) = 2 J

p

f ( h ) h d h hh -p?

n ( r ) = n ( R )

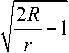
¹d h 2¹arcsin h d h

^J _x h p X h"г ² -p ²

Приведем расчет линзы Итона-Липмана с помощью преобразования Абеля. Для простоты рассуждений и чтобы не учитывать отражение от границы линзы, примем R = 1 и n(1) = 1 .

На рис. 2 показан ход произвольного луча в сферически-симметричной линзе-зеркале:

Первый интеграл в уравнение (27) табличный [12]:

1 dh p 7 h2 -p2

= ln h + 7 h ² -p²|

p

= In

i +71 -p ²

p

Второй интеграл вычислен ранее через производную преобразования Абеля [1] и равен:

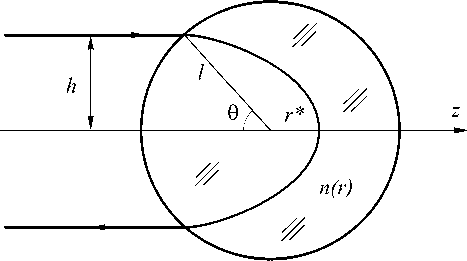
Рис. 2. Ход луча в линзе-зеркале

11 arcsinhdh nJ 7h2-p2

= inVi + Ti-P².

^^^^^^B

Тогда уравнение (27) примет вид:

F ( p ) = In r = In

f    p 2

_v ¹ + 7^{1 -p 2}

Из рис. 2 видно, что любой луч, например параллельный оси z , чтобы развернуться назад и при выходе из линзы иметь направление параллельное оси z , должен проходить в точке лежащей на оси z с наименьшем расстоянием r^* от центра линзы. Тогда общее интегральное уравнение для луча (1) можно записать в конкретном виде для линзы Итона-Липмана:

С учетом того, что ρ = n(r)r , из уравнения (30) получим промежуточное уравнение:

n ²( r ) r ²

1 + 4 1 - n 2( r ) r² ’                              ^{1 1}

решение которого имеет вид:

1     d r     = л - arcsin h

J / 2 .2    72"            h ’ r • r^n r -h h

где h = n(r^*)r^*, r^* – кратчайшее расстояние от луча до центра линзы, h – расстояние от луча до оси z , sin θ = h, θ 2 – θ 1 = π – θ = π – arcsin h, h = n(r)r sin ψ –

/ 2 — r n ( r ) = -----.                                   (32)

r

Решение (32) совпадает с уравнением (22) при n(R) = 1 и R = 1 . Заметим, что при r ^ 0, n (0) ^ « . Особенность в нуле решения (30) делает реализацию линзы-зеркала невозможной. Однако наличие точного решения может облегчить поиск приближенного и реализуемого на практике распределения сферически-симметричного показателя преломления для линзы-зеркала, отражающей назад падающий с любой стороны луч.

3. Интегральные уравнения Абеля для сферически-симметричных градиентных оптических элементов

В работах [9, 6] рассмотрен расчет сферических градиентных оптических элементов, предназначенных для фокусировки излучения, исходящего из точечного источника, в произвольное радиальносимметричное распределение интенсивности в некоторой плоскости за оптическим элементом.

Приведем здесь вывод интегрального уравнения Абеля для такой задачи, но для плоского пучка лучей, падающих на сферически-симметричный градиентный элемент.

На рис. 3 показана оптическая схема.

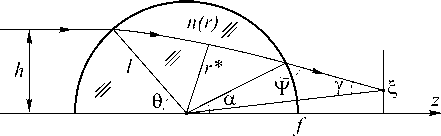
Рис.3. Оптическая схема для расчета сферически-симметричного градиентного элемента, фокусирующего плоский пучок лучей в произвольную радиально-симметричную область с заданным распределением интенсивности в плоскости, отстоящей от центра элемента на расстояние f.

Из рис. 3 можно установить следующие геометрические соотношения (радиус сферы 1, n(1) = 1 ):

sin γ=

sin ψ

J t ² +ξ ²

n dn

∫ I 22   2

1 nn ² r ² - h ²

1      dr

r ^* rn ²( r ) r - h ²

h            ξ

π - 2arcsin h + arcsin          - arctg

_{=                          f 2 +ξ 2} arctg _f

2h где h = n(r*)r*.

Заметим, что в пределе ξ → 0 вместо уравнения (38) получится известное уравнение Моргана [3] для обобщенной линзы Лунеберга:

₁                 2 arccos h + arcsin

∫ dr =                   f

r ^* rn ²( r ) r - h ^{2            2 h}

Уравнение Моргана (39) легко свести к уравнению Флетчера [4], которое более удобно решать с помощью преобразования Абеля [1]:

• ¹    d r _- arccos h ₌

r ^* rn ²( r ) r - h ^{2 h}

h(40)

*                   arcsin

=n∫     dn

1 nn2r2- h22

Для сферически-симметричного градиентного оптического элемента (37) уравнение типа Флетчера (40) будет иметь вид:

h               ξ ( h )

arcsin              - arctg

'I f ² +ξ ²( h ) ^arctg f _{, (41)}

2 h

ξ α=π-ψ-γ+ arctg _f ,

ψ=π-θ=π- arcsin h ,                (35)

где ξ = ξ(h) – точка, в которую приходит луч, отстоящий от оси z на расстояние h и параллельный этой оси до градиентного оптического элемента, r^* – минимальное расстояние луча от центра, h = n(r^*)r^* – параметр луча, который в произвольной точке вдоль по ходу луча внутри оптического элемента имеет вид закона Снелиуса:

h = n ( r ) r sin ψ , (36)

где n* = n(r*), h < 1.

Решать уравнение (41) можно с помощью пары преобразований Абеля (3) и (4).

Для сведения уравнения (41) к уравнению (4) введем           обозначения:            n(r)r = ρ ,

F(ρ) = ln n(r) = ln m(ρ) .         Учтем,         что

F(1) = ln n(1) = ln 1 = 0 . Тогда уравнение (38)

перепишется в виде:

dF( ρ )

- ^{11 d ρ} π ^∫ _x ρ 2

dρ

-

h ²

¹ S( h ) ,

π

где ψ угол между лучом и радиусом.

Из рис. 3 видно, что часть луча внутри оптического элемента симметрична относительно радиуса r^* , при котором угол ψ равен π I 2 , поэтому в уравнении (1), которое верно для любого луча в градиентной среде со сферически-симметричным показателем преломления, достаточно выбрать половину части луча от r 2 = r^* до r 1 = 1 , при этом:

где:

h               ξ ( h )

arcsin              - arctg

S( h ) = arcsin f ² +ξ ²( h ) ^arctg f

2 h

Уравнение (42) с точностью до обозначений совпадает с уравнением (4). Тогда функцию F(ρ) можно найти с помощью уравнения Абеля (3):

∆θ = θ2

- θ1=

π-θ-α

_{F( ρ ) =} 2S( h ) h d h

π_ρ у h ² -ρ ²

Тогда уравнение (1) с учетом выражений (37) и (33) – (35) примет вид:

Тогда, в прежних обозначениях, вместо уравнения (44) получим:

где:

n ( p ) = exp Ф 1 ( р )ехр Ф 2 ( Р ),

Заключение

arcsin

Ф1 (Р) = -|------

h

_ _ f² + S 2 ( h ) _

d h

,

V

Ф 2 ⁽ Р ) =--I

П J p

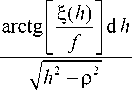
ρ = n ( r ) r .

Аналитически интегралы в выражениях (46) и (47) не берутся, но они могут быть вычислены численно. Функцию ξ(h) можно получить из условия сохранения энергии:

h                             S

J I o ( h ' ) h' d h' = C ² J Ш'd S ,             (48)

где I 0 (h) и I 1 (ξ) - распределения интенсивности в падающем плоском пучке и в плоскости фокусировки, соответственно. Например, для случая фокусировки плоского пучка с постоянной интенсивностью I 0 в фокальную круглую область также с постоянной интенсивностью I 1 , из уравнения (48), следует связь между ξ и h :

S =

0 _{h .}

Константа C определяется из граничных условий: крайний луч при h = 1 должен попадать в крайнюю точку фокального круга при ξ = ξ 0 , тогда

С - 1 =S o

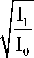
Для фокусировки плоского пучка с гауссовой

( h 2 )

интенсивностью I₀ ( h ) = I₀ exp II в фокальный I ^ю )

круг с постоянной интенсивностью I 1 (ξ) = I 1 из уравнения (48) нетрудно получить связь между параметрами h и ξ :

_ to Io i

S =--- 1 - exp

ю

. ю2

С

I

.

В работе получены следующие результаты:

• •    С помощью интегрального преобразования Абеля в рамках геометрической оптики получены и решены интегральные уравнения для известных линз со сферически-симметричным распределением показателя преломления: линзы Максвелла «рыбий глаз» и линзы Итона-Липмана.

• •    Получено решение задачи расчета градиентного оптического элемента со сферически-симметричным распределением показателя преломления, который фокусирует плоский пучок света в радиально-симметричную область с заданным распределением интенсивности, находящуюся на некотором расстоянии от элемента в плоскости, перпендикулярной оптический оси падающего пучка.