Преобразование Абеля в задачах синтеза градиентных оптических элементов

Лунеберг [ 1 ] нашел зависимость показателя преломления от радиуса в сферической системе координат, при которой все лучи, выходящие из точки с единичным радиусом, сходятся в диаметрально противоположной точке также на единичном расстоянии от центра. Если на такую градиентную сферическую линзу Лунеберга направить пучок параллельных лучей, то все они соберутся в точке на поверхности линзы.

Флетчер [ 2 ] и Морган [ 3 ] получили разные виды интегрального уравнения для обобщенной задачи Лунеберга. Если параллельный пучок лучей падает на обобщенную линзу Лунеберга, то все лучи сходятся в точке на оси внутри или снаружи сферической поверхности линзы. Решение для обобщенной линзы Лунеберга с помощью преобразования Абеля, а также для других типов обобщения задачи Лунеберга найдены в [ 4-7 ] . В [ 6 ] решена задача расчета сферического градиентного аксикона. В данной работе показана связь между уравнениями Моргана [ 3 ] и Флетчера [ 2 ] , а также, с помощью производной от преобразования Абеля, из решения для обобщенной линзы Лунеберга получен показатель преломления для обычной линзы Лунеберга.

В [ 8 ] Микаэляном была решена задача нахождения показателя преломления для цилиндрической градиентной линзы. Если на такую линзу падает параллельный пучок лучей (перпендикулярно одной поверхности линзы), то все лучи соберутся в точку на оптической оси на другой поверхности линзы (или до этой поверхности внутри линзы). В данной работе для обобщенной задачи Микаэляна, когда параллельные лучи сходятся на оптической оси за поверхностью линзы, получено интегральное уравнение типа уравнения Абеля. Для цилиндрического градиентного аксикона также получено интегральное уравнение, которое сведено к более простому трансцендентному алгебраическому уравнению. Кроме того, решение для линзы Микаэляна в этой работе получено с помощью обращения преобразования Абеля.

Сферические градиентные оптические элементы (ГОЭ)

Для среды с показателем преломления n = n ( r ), зависящим только от радиальной координаты r в сферической системе координат, имеет место лучевой инвариант, который является обобщением обычного закона преломления Снелиуса [ 9 ] :

/ , 2 d^ , n (r) r — = h = const dl                .                               (1)

Уравнение (1) выполняется вдоль траектории луча. На рис. 1 показан ход луча (и обозначения) в обобщенной линзе Лунеберга. Все лучи, параллельные оси z , должны сходиться в точке на оси и на расстоянии f от центра линзы.

Радиус линзы r = 1, n (1) = 1, h – расстояние от оси до выбранного луча, r * - минимальное расстоя-

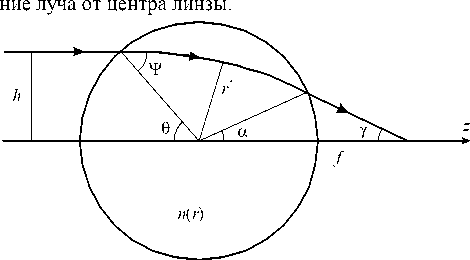
Рис. 1. Ход луча в обобщенной линзе Лунеберга

Из рис. 2 видно, что приращение d l вдоль траектории луча связано с приращением по радиусу d r и углу d e следующим образом:

d l = V( dr ) ² + ( rd e ) ² .

Из уравнения (2) следует:

d l     / ₂ ( dr ) 2

= r 2 +1 I

de ]    Ide J

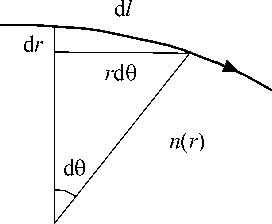
Рис. 2. Участок траектории луча в градиентной среде

Подставим выражение (3) в уравнение (1), получим:

-dr = r-jn ²( r ) r ² - h ² .                        (4)

d 9 h

Из уравнения (4) следует интегральное уравне- ние для поиска показателя преломления в произвольной сферической градиентной среде:

J , dr        = ¹ J 2 d 9

r , r^n²(r ) r ² - h^{2    h} 9 1

Интегральное уравнение для обобщенной линзы Лунеберга

Интегральные уравнения для расчета показателя преломления обобщенной линзы Лунеберга были получены в [ 2, 3 ] . Требуется найти n ( r ), чтобы параллельные оптической оси лучи сходились на оси в точке на расстоянии f от центра сферы с радиусом r = 1 (f > 1). Из рис. 1 видно, что r , = r * , n ( r * ) r * = h .

d 9

Так как r = sin^ (см. рис. 2), то лучевой инвари-dl ант (1) можно записать в виде n(r)r sin^ = h .

Граничные условия равны: при r = 1, n (1) = 1, тогда sin ^ = sin 9 = h ; r ₂ = 1; 9 , - 9 2 = A 9 = ^{п - a - 9} ;

arcsin h h                             y1

sin— =  ; a = 9 - - , A9 = l- - 9l + - = arccos h +— f                  12 J 22

.

Все последние равенства нетрудно получить из гео-

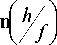
метрии на рис. 1.

Тогда уравнение (5) в частном случае для обобщенной линзы Лунеберга можно записать в виде:

.        ,           2arccos h + arcsi

1        d r       =

r * r^n ²( r ) r ² - h ^{2               2 h}

**

где h = r n ( r ).

Это уравнение было получено Морганом [ 3 ] . Аналогично, можно получить уравнение Флетчера [ 2 ] :

2 h

1       d r         n-       d n

^J 22,2 ^J 22,2

r Hn r - h 1 nyn r - h

¹       n d r ⁿ       r d n

^J       22,2 ^J       22,2

r nrjn r - h 1 rn\n r - h

1 n d r + r d n

22 h nr^n r - h

J

h

d( nr )

( nr)^(nr )² - h ²

j df h^^- h2

arccos h h

Последнее равенство в уравнении (8) следует из табличного интеграла [ 10 ] .

Прямое и обратное преобразования Абеля

Чтобы решить уравнение (7) с помощью преобразования Абеля приведем некоторые предварительные сведения. В [ 11 ] дана пара (прямое и обрат -ное) преобразований Абеля с верхним бесконечным пределом:

^

F( r ) = 2 J

r

f( x ) x d x

dF( r )

^

f( ^ ) =- - J п

x

d r

d r

^^^^^^в

x ²

.

Заметим, что повторное применение преобразования (9) к уравнению (10) приводит к выражению для производной от преобразования Абеля:

dF( r ) d r

df( x )

^      d x

= 2 r j , d *

r >1 x ² - r ²

В [ 12 ] приведена другая форма обратного преобразования Абеля с верхним бесконечным пределом. Вместо уравнения (10) можно записать:

то

J- xr

1d

^f( * ) = ^-      *

п d x

F( r )d r

A r ² - x²

Если приравнять правые части выражений (10) и (12), то можно получить полезные выражения для производной от преобразования Абеля:

Г dF - F Y d ^то F( r )d r = 1 ^то^ d r   r J

d * x r^r ² - x ^{2    x} x ^r ² - x ²

df( x ) dTO                  то „   d x

_ c ^{f( x} ) ^x d x = r г d x dr ^J 2     2 ^J ГЧ. 2 .

' r rjx - r      r \x - r

Для прямого и обратного преобразований Абеля в конечных пределах в [ 13 ] даны следующие выражения:

r

F( r ) = J

f( x )d x r -V r - x

Г        ,dF( ^ ) dr

f( x ) = 1 F⁰) + J n V x о V x - r

r      dx r 7(x- r)(r'- x)

Заметим, что в уравнении (15) преобразование Абеля представлено в виде свертки и поэтому для его обращения можно использовать преобразование Фурье, с учетом того, что функция 1 является

На основе преобразований Абеля (18), (19) можно получить две разные формы для производной от преобразования Абеля. Первая форма для производной приведена ранее в работах [ 4-6 ] . Для ее получения возьмем по частям интеграл в преобразовании Абеля вида:

инвариантной по отношению к преобразованию Фурье [ 14 ] :

F( r ) =

¹ f( x )d x

J Г~2 2 r Nx - r

1- [ f( x ) x ] d x

J    ГЧ    2"

r x\Jx - r

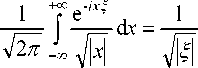
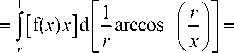
f(1)arccos ( r )

В интегральных уравнениях (6) и (7) пределы

r

интегрирования отличаются от пределов интегрирования в уравнениях (15) и (16), поэтому приведем пару преобразований Абеля в конечных пределах, удобных для решения уравнения (7):

— I arccos r_r

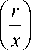
« x , df д f( x ) + x — d x .

d x

F( r ) = ^« x S. .

r Nx 2 - r

" dF( rК

f( * ) =- M r — - -.FdL

* ^j-Nr ² - x ² e x

При получении уравнения (23) использовалось соотношение:

d d x

1 f r — arccos l — r ( x

x\x - r

Дифференцируя выражения (23) по r , получим:

Проверим, что уравнение (19) является обращением преобразования (18). Действительно:

, ^df( x ) xdx dF( r ) = 1 1 d x x d x - f(1) ^d r   r ^J7 x ² - r ²   1-^7

F( r ) = J

r

f( x )d x ²

7 x ² - r ²

=-1J

JJ xr

dF

— d r d x ²

d r

V( r' ² - x ² )( x ² - r ² )

> =

П

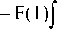
r

d x ²

7(1 - x ²)( x ² - r ²)

i dF л /f         d x ²

— d r ,

I l x ^{d r}     /2 7( r' ² - x ²)( x ² - r ²)

> =

Если исходить из преобразования Абеля в виде выражения (18), то вместо (25) можно получить другой вид производной от преобразования Абеля. Выполняя интегрирование по частям в уравнении (18), получим:

F( r ) = 2f(1)71 - r ² - 217 x ² - r ² dfd x .     (26)

d x

Дифференцируя уравнение (26) по r , получим:

dF( r ) = 2 r d r

df( x )

1 d x d x

^J ГЧ 2 r N x - r

f(1)

TT- r²

F(1) J dx r27(1 -x2)(x2 -r2)

= --Ы —d r '- n F(1)[ = F( r ) . n ^J d r '

I x

В уравнении (20) предпоследнее равенство получено на основе табличного интеграла [ 10 ] :

d x               . ( r + r ^,-2 x )

= = - arcsin---:-----:---

' x - r )( r '- x )                 r '- r

который в конечных пределах дает следующий результат:

Производная от преобразования Абеля в виде выражения (25) будет использована при получении решения для обычной линзы Лунеберга [ 1 ] .

Решение интегрального уравнения для обобщенной линзы Лунеберга

Будем исходить из уравнения Флетчера [ 2 ] . Перепишем уравнение (7) в другом виде:

*

j   dm n ( r )     = f₍ h ),

1 7 n 2 ( r ) r ² - h²

где

1         ■ hh

f( h ) = — arcsin I —

2 h     I f

Введем обозначения:

верхности линзы), тогда вместо уравнения (32) получим:

In n ( r ) = F( r ), n ( r ) r = p , F( r ) = F( p ). Тогда вместо (28) запишем:

- n

h

dFMdp dp p2       2

= -f( h ) . К

dln n ( p ) ₌ 1         1

d p  " 2 p М1³ 7 2 _ .

Интегрируя уравнение (33), получим:

In n ( p ) = lnJ1 + 1 - - p , p = n ( r ) r .

С учетом того, что F(1) = ln n (1) = ln1 = 0, урав-

нение (29) с точностью до обозначений совпадает с уравнением (19), и поэтому для его обращения можно использовать уравнение (18). Тогда получим:

При выводе уравнения (34) использовался табличный интеграл [ 10 ] :

F( p ) = - j ⁿ p

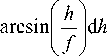
d x

22 x\a - x

1 , a + V a - x

- ln ax

Из уравнения (30) для показателя преломления обобщенной линзы Лунеберга, представляющей собой радиально-симметричную градиентную сферу, фокусирующую параллельный пучок лучей в точку (рис. 1), будем иметь [ 6, 7 ] :

1 f n ( p ) = exp I —

ТГ •*

■ I x L arcsinl — I d x

I f J

x - p

где p = n ( r ) r .

Решение для обычной линзы Лунеберга с помощью производной от преобразования Абеля

Интеграл в уравнении (31) не берется в аналитических функциях даже при f = 1 (случай обычной линзы Лунеберга [ 1 ] ). Однако производная от функции показателя преломления (31) может быть записана в элементарных функциях. Действительно, используя выражение для производной для преобразования Абеля (25), получим:

d I • x\       ■ 1

x—arcsin— Idx arcsin— dn(p) = n(p) I f dx I     f J f -= dp   n I p   7x2 - p2    Tw

Из уравнения (34) нетрудно получить функцию показателя преломления для линзы Лунеберга единичного радиуса [ 1 ] :

n ²( r ) = 2 - r ². (36)

Цилиндрические градиентные оптические элементы

В [ 8 ] Микаэляном получено и решено интегральное уравнение для бесконечного цилиндрического ГОЭ, собирающего все лучи, исходящие из точечного источника на оптической оси, в точки на оптической оси, расположенные периодически. Для конечного ГОЭ длиной L задачу Микаэляна можно сформулировать как задачу Лунеберга для сферического ГОЭ. Требуется найти n = n ( r ), r – радиальная координата в цилиндрической системе координат, который фокусирует параллельный поток лучей, падающих перпендикулярно на поверхность цилиндрического ГОЭ, в точку на оси на противоположной стороне ГОЭ (см. рис. 3).

[                                                   1 1

1                          arcsin n (p) 1 f        dxf :

П I ² ' ^ ( x ² - p ²)( f ² - x ² )  TW

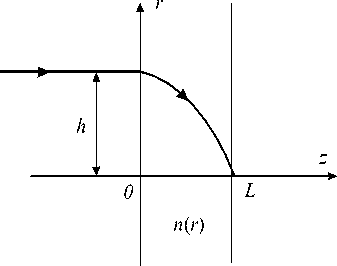
Рис. 3. Ход луча в цилиндрической линзе Микаэляна

Для цилиндрической задачи лучевой инвариант, аналогичный выражению (1), имеет вид закона преломления Снелиуса [ 9 ] :

n ( r )cos 9 = n ( h ) = const, (37) где h – расстояние от оси рассматриваемого луча при z = 0.

В уравнении (37), которое выполняется вдоль луча, учтено, что при z = 0 угол 9 для всех лучей равен нулю. Из рис. 4 видно, что имеет место связь между приращениями:

n(p) П 1 =-^I---arcsin np 4 2

( p ² + f 2 - 2 )

I p² - f 21

■ 11 arcsin

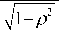
Заметим, что уравнение (32) в [ 4 ] получено в другом виде. Далее используя уравнение (32) можно получить решение для классической (обычной) линзы Лунеберга. Для этого в уравнении (32) положим f = 1 (фокусировка параллельного пучка лучей на по-

d r = tg e = I -22- - 1 = I^r - 1 .

dz         V cos² 9       У n ² ( h )

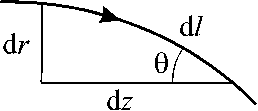
Рис. 4. Приращение вдоль траектории луча

Из уравнения (38) следует интегральное уравнение относительно n ( r ) для линзы Микаэляна:

0L f , '     -fd=-L.

h n ( r )          0

^{- 1}

n ²( h )

Интегральное уравнение для обобщенного цилиндрического ГОЭ

Как решения Моргана [ 3 ] , Флетчера [ 2 ] и Флореса [ 4-6 ] обобщают линзу Лунеберга [ 1 ] , также можно попытаться обобщить решение Микаэляна [ 8 ] . В [ 15 ] , например, рассмотрены составные цилиндрические ГОЭ, являющиеся обобщением линзы Микаэляна и предназначенные для фокусировки параллельного пучка лучей в произвольное радиальносимметричное распределение интенсивности на задней поверхности ГОЭ.

Получим уравнение для обобщенной линзы Микаэляна. Требуется найти функцию n = n ( r ) для цилиндрического ГОЭ, фокусирующего падающий параллельно оси z пучок лучей в точку на оси за оптическим элементом на расстоянии f (см. рис. 5).

В [ 8 ] Микаэлян подбором нашел решение уравнения (39) и заметил при этом, что уравнение (39) нельзя отнести к определенному типу интегральных уравнений. Но это не совсем так. Покажем, что уравнение (39) можно решить с помощью преобразования Абеля.

Перепишем уравнение (39) в виде:

I

h

d r

V n ²( Г ) - рР

L

,

р

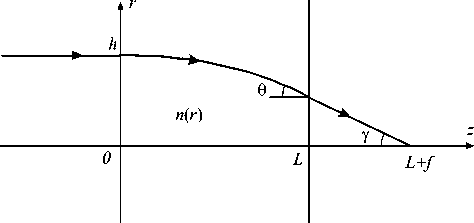
Рис. 5. Ход луча в обобщенной линзе Микаэляна

где р = n ( h ). И введем обозначения: n ( r ) = x , r = m ( x ). Тогда уравнение (40) можно переписать в

виде:

n (0)

ⁿ p

dm(x) dx dx        L

=- x 2 - о 2    nP

.

С учетом того, что m ( n (0) ) = r = 0, уравнение (41) отличается от уравнения (19) только обозначением. Тогда, применяя обратное преобразование (18) к уравнению (41), получим:

n (0)

m ( x ) = — f n

x

dp

x ²

п

p - x

n (0)

2 L

= —ln п

x

' n (0) + 7 n ²(0) - x² '

x

.

Рассуждая аналогично, вместо уравнений (39) и (40) получим уравнение для обобщенной линзы Микаэляна:

h1        dr h n 2( r) - n 2( h)

L

n ( h ) ^,

где h – радиальная координата луча во входной плоскости, h ₁ – в выходной плоскости (см. рис. 5).

Из рис. 5 также можно получить еще одно уравнение, связывающее координаты h и h ₁ :

h n (h1)sin9(h1) = sin / = .

V f ² + h 1 ²

n ( h 1 )sin 9 ( h 1 ) = n ( h ) .                              (47)

V

Из уравнения (42) следует:

n (0) + V n ²(0) - n ²( r )

Уравнение (46) – это закон преломления Сне-лиуса, примененный к выходной поверхности, а уравнение (47) – это лучевой инвариант (37). Исключая из уравнений (46) и (47) угол 9 , получим:

n ²( h 1 ) - n ²( h ) =

n ( r )

I nr ) = expl      I .

12 L J

h 1 ²

h 1 ² + f ²

С помощью замены переменных: n ( r ) = x ,

Из уравнения (43) нетрудно получить решение

Микаэляна [ 8 ] :

n ( h ) = p , n ( h 1 ) = p 1 , r = m ( x ), уравнение (45) можно

привести к уравнению Абеля:

n (0) n ( r ) = ~^

, ' nr ch|

V 2 L

.

f

о

d m ( x )

d x d x

L

,

о

где:

где:

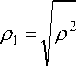
+ m i

⁺ m 2 + f ²

m 1 = m ( p 1 ) = h 1 .

В отличие от стандартного уравнения Абеля (19) в уравнении (49) верхний предел интегрирования не является постоянной величиной, а зависит от нижнего предела интегрирования, поэтому применять для решения уравнения (49) стандартную формулу обращения преобразования Абеля (18) нельзя.

Обращение преобразования Абеля с двумя переменными пределами интегрирования

Общий случай

Попытаемся с помощью преобразования Фурье найти формулу для обращения преобразования Абеля с двумя переменными пределами интегрирования. Будем исходить из преобразования Абеля вида:

F( p ) = 2 J f⁽ x ) x d x p -V x - P

где p 1 = p 1 ( p ). Введем замену переменных: x ² = y , p ² = в , pp 2 = p 1 , тогда уравнение (51) перепишется

в виде интеграла свертки:

2 y - a L в «       ” rect       If(y)dy

F( в) -J-S± ,       '----, в Vy- в -”    y-- в

где: F( P ) = F( p ), f( y ) = f( x ), B = ^ ^, A = p ^.

Заменим в уравнении (52) все функции на их Фурье-образы:

to

Ф(ф) = JF(P)e'py dp,(53)

to to f (y) = JS(5)ey5 5 d^,(54)

to

2v- A А rect------1 = 2B J sinc(Bn)e (y )n dn,(55)

V ^J

1           i ” e i ⁽ y ^- P^)

--- = ^= —    d t .

Q ( n , t + to ) = J [ 2 B ( P ) sinc ( B ( P ) ) p ] •

• e - iA (P^ e - i P ⁽ t +^{to )} d p

5 - дельта функция Дирака.

Частный случай

Уравнение (57) в общем виде не позволяет воспользоваться преимуществом интеграла свертки, но это можно сделать для частного случая зависимости функций B( в ) и A ( в ) от в.

Предположим, что верхний и нижний пределы в первом интеграле (52) связаны простой формулой:

P i = в + 2 M ,

тогда B ( в ) = M , А ( в ) = p + M и интеграл (58) вычисляется в явном виде:

Q(n, t + to) =

= 2 M sinc M n e ^{M n} J e •"" t ^{+to )}d p =

-to

= [2 M sinc M n]e-'M15(n +1 + to).

Тогда уравнение (57) можно переписать:

_ф ( _у ) = jj S^(- n ^-ф M s^inc M n ]

•

• e i^{M n} 5 ( ® + n + 1 ) d n d t =

, to [ 2 M sinc M n ] e ^{- iMn} , = S( ® ) J ----/ ।       ।----d n =

-to     л/2 Пп + ® l

= S( ® )U( ® , M ).

Уравнение (61) позволяет легко найти функцию S( с у ), а также, с помощью преобразования (54), и искомую функцию f ( y ):

f( y ) =Ь? У ф ' ^{у ю} a ® , to u( ® , m )

где:

to

U( y , M ) = J

-to

[ 2 M sinc Mn ] e i^{M n} d =

M

= e ^{M y} J

M

-

_e i 5®

3 _M

2 e it у d 5 = J   ,— d t .

Тогда вместо уравнения (52) получим: _ф у = J _ J ^{S( 5 ) [} 2 ^{B sinc( B} n ^{) ]} _e iy ( 5+n + 1 ) 72 ^^

Ie- iA n

•

Интеграл (63) можно свести к табличным интегралам Френеля (заменой переменной t = p ²):

₂ 3 _{M    2}

- i B t

• e ^в e

-I

' ^py d ^ d n dt d ^ d y =

= _JJJ ^S   Q ' ⁿ  +У5⁵ + ^{n +} t > d n t =

U( ® , M ) = 2 J e ^{i m p} d p = 2U 1 ( ® , M ) =

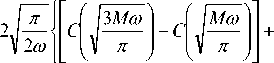
_{= JJ} S ⁿ t ^Q d t + ® ) d n d t ,

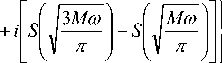
где табличный интеграл Френеля имеет вид:

с ( x ) =

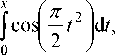
Тогда формула обращения преобразования

Абеля (66) для аксикона будет иметь вид:

x

I П 2 I

S ( x ) = J sin l —t ² I d t .

0 ^{V 2}    )

d m ( x ) = l C r^{e i mP} x ) d p d ® 2 x d x      J^J   U 1 ( ® , M )

.

Интегрируя уравнение (71), получим:

В исходных обозначениях выражение (62) для обращения преобразования Абеля (51) при условии (59) имеет вид:

X я ^{n (0} )      ₂ ^{n (0} )

m ( x ) = - L f--------- f e ^l ® y d y f e

-^JX U 1 ( ® , ^V ) ^{J 7J}

-)

i ® ^{p 2} d p =

,^X_r F( p )e - ® ^{p 2}- x ² )

f⁽ x ) = I I тт^        P d P d ® .

00    U i ( ® M )

X

= -L J d®

-X

(e i ® n ² (0)

i®

e ® 2) V 1 ( ® , n (0))

U 1 ( ® , V ) ’

где:

Интегральное уравнение для цилиндрического градиентного аксикона

В отличии от обобщенной цилиндрической линзы, показатель преломления которой ищется из уравнений (47) и (48), для аксикона, который все лучи параллельные оптической оси и отстоящие от неё на расстоянии h , собирает в точке на оптической оси, отстоящей от второй поверхности ГОЭ на рас-

V3 sin V

U i ( ® , V ) = J sin V

n (0)

V 1 ( ® , n (0)) = J

e ® d p ,

e

-)

i ® ^{p 2} d p .

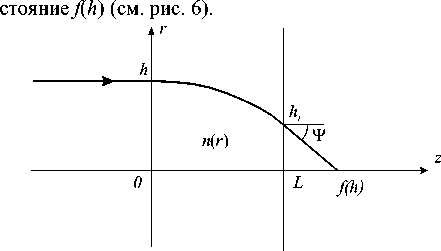
Рис. 6. Ход луча в градиентном аксиконе

Так как все лучи, выходящие из ГОЭ аксикона, должны иметь одинаковый угол V , то вместо уравнения (46) для аксикона получим:

Функции U 1 и V 1 также как и функция U( ®, M), сводятся к интегралу Френеля. Переходя к исходным обозначениям, окончательно вместо (72) получим:

r = iL X d®^2(0)

-X ®

i ® n ² ( r )1 V 1 ( ® , n (0))

e ] U 1 ( ® , V ) . ⁽⁷⁵⁾

Решим уравнение (75) для «слабого» аксикона.

Пусть n ²( r ) = n ²(0) -A n ²( r ), где A n ²( r ) << n ²(0).

Тогда уравнение (75) можно упростить:

i ^X 2

= i J d ® e ® n ⁽ ) A n ²( r ) R ( ® , n (0), V ) ,

-X

где:

n ²( h 1 ) - n ²( h ) = sin² V .

Тогда пара уравнений для нахождения показателя преломления цилиндрического аксикона будет

R ( ® , n (0), V ) = V L ( ® n 0)

U₁( ® , V )

Из уравнения (76) следует, что:

.

иметь вид:

d m ( x )

P i —d x d x

J Г2    2"

руx -р

n ²( r ) = n ²(0) +

r

L

,

Р

LW ( n (0), V )’

p i - р ² = sin² V .

где:

n ( r ) = V n ²(0) + [ LW ( n (0), V )] ^{- 1} r ,

Чтобы воспользоваться формулой (66) для решения уравнений (68) и (69), необходимо использовать связь обозначений

X

W ( n (0), v ) = J R ( ® , n (0), V ) e i ® "^{2 (0)} d ® .

-X

d ^ ' x ' = 2 f ( x ) x , x

F( P) = - ^L , P

„ sin² V

M =       .