Преобразование геометрических условий в аналитические при решении планиметрических задач

В геометрических задачах нередко часть условий представлена либо косвенным образом, либо в виде словесного описания особенностей заданной конфигурации. Статья посвящена рассмотрению приемов перевода таких условий на аналитический язык.

' А. К Sereda

Transformation of geometrical conditions in analytical ones at the decision of planymetrical tasks

It is quite often in geometrical tasks that part of conditions is represented or by an indirect image, or as the verbal description of features of the given configuration. This article is devoted to consideration of receptions of translation of these conditions on analytical language.

Считается, что задача сформулирована корректно, если в ней нет "лишних" условий (т.е. условий, которые можно не использовать для решения задачи), а те условия, которые даны, достаточны для ее решения. Поэтому при решении любой корректно поставленной задачи нужно использовать все ее условия. Игнорирование (или неправильное понимание) того или иного условия обычно является основной причиной затруднений в решении задачи.

В геометрических задачах нередко часть условий задана либо косвенным образом, либо в виде словесного описания особенностей заданной геометрической конфигурации. В последнем случае очень важно перевести эти условия на аналитический язык. Часто именно этот этап решения является ключевым, так как позволяет выяснить характерные особенности заданной конфигурации [1]. Проиллюстрируем эти соображения двумя примерами, взятыми из практики вступительных экзаменов на механико-математическом и экономическом факультетах Новосибирского государственного университета.

Пример L В треугольнике ЛВС известны длины сторон: АВ = 7, ВС = 8, АС = 9. На стороне АС выбрана точка М так, что окружности, вписанные в треугольники АВМ и ВМС, касаются друг друга. Найти, в каком отношении отрезок ВМ делит площадь треугольника АВС.

В                    Решение. Для решения задачи достаточно знать, в j                   каком отношении точка М делит сторону АС.

|   ■                Обозначим через Р точку касания окружностей,

1    ■             вписанных в треугольники АВМ и ВМС. Очевидно,

/ _ I         "          что Р е ВМ.

;4            Переведём на аналитический язык условие касания

/        । р _;        окружностей. Введём обозначения: AM =х, ВМ= I.

1ф          '           Используя свойство окружности, вписанной в г ' _ треугольник, для треугольника АВМнаходим, что

Рис. 1                                      ■

^-^ (АВ + ^^ + ^) ~ А М = ^ (7 + 1 + х) - Л = ^^-, а из треугольника ВМС определяем ещё одно соотношение для этой же величины:

ВР=Х^(ВС\МС^ВМ^МС-Х-^

'                            7 + I-х I -v x-Y

Таким образом, получаем равенство ——---=        , которое является аналитическим эквивалентом условия касания окружностей, вписанных в треугольники

5     4

АВМ и ВМС. Отсюда находим, что х = 4. Следовательно, АМ = 4, МС = 5 и ^^- = —.

° ВМС

Ответ;

S др^   4

^ВМС 5

Пример 2. В трапеции A BCD основание АВ равно 2, угол А равен 60°, а угол В равен 30°. Известно, что биссектрисы углов А и D трапеции и высота СМ, опущенная из вершины С на основание АВ, пересекаются в одной точке. Найти площадь трапеции.

Решение. Произвольная трапеция определяется четырьмя параметрами. В данном случае явно заданы три, а четвёртый "скрыт" в условии пересечения биссектрис углов А и D на высоте СМ трапеции. Чтобы решить задачу, этому условию надо придать аналитический вид.

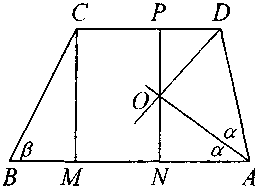
Рис. 2

Рассмотрим сначала произвольную трапецию ABCD (рис. 2). Обозначим: СМ = h, ВМ = х, О- точка пересечения биссектрис углов А и D. Опустим из этой точки перпендикуляры ОР и ON на основания трапеции. Так как точка О равноудалена от h сторон CD, AD и АВ, то ОР = ON = —. Из треугольника ВСМ определяется, что h — x* tgP, а из треугольника AON находим, h X'tgB                          л что AN = — — =--—— . Условие принадлежности точки О

2 Oga 2- tga высоте СМ означает, что точки М и N совпадают и ВМ + AN = АВ. Таким образом, аналитическим выражением условия пересечения биссектрис углов А и D на высоте СМ tgB является (в наших обозначениях) равенство х + х—■---- — АВ.

■                   2 • tga

Применив полученное равенство к условиям нашей задачи (АВ = 2, а= Д конкретное значение величин углов на данном этапе решения С D значения не имеет), получаем соотношение !......з                   4

i   ;          — Х- 2 ИЛИ X = —.

:      :                  2                          3

;           Опустим из вершины D высоту DE на основание

'                  i i ■ АВ. Дальнейшее очевидно:

D . М Е A          h = --tg3O° = - * =

Рис-3                        з з 7з з^'

4    14

АЕ = h • ctg60° = —= —, зТз V3

4 4 2

CD - ME = 2 - ВМ - АЕ = 2---- -.

3 9 9

Р.И, Сунгатуллина. Готовность учителя математики к деятельности по развитию математических способностей учащихся общеобразовательной школы                  119

Таким образом, 5 = — (2 + —)--=-----

2     9 Зл/З 81

о 40V3

Ответ; о = ~-----.