Преподавание – это искусство

Князь Болконский: «Чтобы развить деятельность и ум, давал своей дочери-княжне Марии уроки алгебры и геометрии».

(Л. Толстой «Война и мир». М., т I.)

В условиях быстрого роста количества научной информации и столь же быстрой ее переоценки особую важную роль играет фундаментальное математическое образование не только инженеров специалистов. В настоящее время уже достоверно известно, что результаты любой науки будут обоснованными, точными только в том случае, когда исследование их основывается на математике. Развитие во всех сферах, т.е. всеобщее развитие тесно связано с состоянием математического образования.

Например, известно, что в пятидесятых - шестидесятых годах прошлого века в СССР получило бурное развитие космонавтика и ещё известен тот факт, что олимпийская команда учеников в стране по математике имели отличные успехи за эти годы. То же самое, можно говорить и о китайском феномене.

Обучение – это сложный процесс.

Потому, что каждая дисциплина или наука имеет свою специфику в том числе и математика. Математика как дисциплина, пишет Б. В. Гнеденко, требует строгой последовательности в приобретении знаний, а в литературе, например, на много проше, т.е. можно приступить к изучению творчества Пушкина, имея слабое представление о творчестве Шекспира [1].

Учитель не только учит детей, преподаватель не только преподаёт урок, этого мало, т. е. они должны установить взаимопонимание со своими учениками. Они должны вызвать интерес учащихся при процессе занятии. Их задача не только преподать урок и обеспечить их информацией. Одним словом, в процессе обучения требуется мастерство учителя, преподавателя. Здесь так же играет важную роль простота и доступность [3].

Следующий пример подтверждает, насколько важно мастерство учителя:

В одном из прибалтийских республик в 1906 году шестилетняя девочка вместе с отцом на крыше своего дома с помощью самодельного телескопа наблюдали на небе комету Икар. Девочка в будущем выросла и стала учительницей математики, физики и астрономии, и известен такой факт: все ее ученики одного выпускного класса (около тридцати учеников), в 1936 году поступили в Московский университет как одна группа физического факультета. Комментарии излишни.

Когда речь идёт о простоте материалов уместно вспомнить слово Д. Гильберта. «Выкладки на лекции должны быть на уровне таблицы умножений» [2].

В процессе обучения на каждом занятии необходимо вызвать интерес слушателей. Приведём некоторые примеры, не идеальные, конечно, а просто примеры.

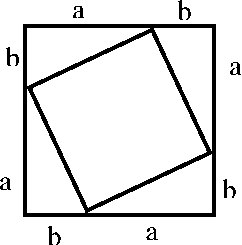
О теореме Пифагора. В настоящее время известно около двухсот доказательств разного вида этой теоремы. Ниже вспомним один из самых простых вариантов доказательств формулы Пифагора.

( a + b ) 2 = 4 • — ab + c²

Из рисунка видно, что площадь квадрата равна 2 , а после не сложных упрощений получим то, что надо: ^a 2 ⁺ b ² = c ².

Об арифметической прогрессии. Допустим, тема урока – арифметическая прогрессия. При этом возможно, что учитель после объявления темы, будет объяснять определение этого понятия. Затем начнёт вычислять и строить формулу общего члена и суммы первых n членов прогрессии. Конечно, этот процесс сопровождается необходимыми примерами. Можно признать, что вполне нормальный урок.

А опытный преподаватель сначала будет приводить несколько примеров на числовые последовательности, и просит выделить среди них таких как, имеющих определенные закономерностеи по изменению членов последовательности. Объяснит определение понятия арифметической прогрессии.

После, предложит найти сумму от 1 по 10. Конечно, ученики быстро найдут ответ. А потом просит также быстро найти суммы чисел от 1 до 100. Но ученики на этот вопрос не сразу будут отвечать. И здесь можно рассказать, что юный И. Гаусс как решил такую задачу:

S = 1 + 2 + 3 + ... + 99 + 100

100 + 99 + 98 + ... + 2 + 1

2 S = 101 •ЮС = 10100, S = 5050.

Этот пример убедительно показывает, что математика - именно наука об умении нахождения способов, методов решения примеров, задач и проблем.

Числовые последовательности. Возможно, будет интереснее, если начинать урок с одной древней задачей [4].

Сколько пар кроликов в один год от одной пары рождается?

Некто поместил пару кроликов в некоем место, чтобы узнать, сколько пар кроликов родится при этом в течение года, если через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения. Так как первая пара в первом месяце даёт потомство, удвой, и в этом месяце окажутся 2 пары; из них одна пара, а именно первая, рождает и в следующем месяце, так что во втором месяце оказывается 3 пары, из них в следующем месяце 2 пары будут давать потомства, так что в третьем месяце родятся ещё 2 пары кроликов и число пар кроликов в этом месяце достигнет 5 и т. д.

В результате имеем следующий числовой ряд:

• 1,    1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377.

Итак, в последнем месяце они дают 377 пар. Эти числа называются числами Фибоначчи.

В общем виде рассмотрим следующую числовую последовательность:

• ^{1, 2,.., n} , в которой каждый член равен сумме двух предыдущих

членов, т. е. n >  ² U n = U n - 1 ⁺ U n - 2 .

О введении к теории вероятностей. Прежде чем перейти к изложению основных понятии теории вероятности можно рассказать о том, как пришёл Б. Паскаль к понятию вероятности [5].

Некий игрок в кости француз придумывал новые правила игры. Он выиграл если при четырёхкратном бросании кости хотя бы один раз выпадало 6 очков. Ради интереса он обратился к своему другу, математику Б. Паскалю изучить эту игру и оценить шансы его на выигрыш.

Его рассуждения заключаются в следующем. Мы знаем, что игральная кость – это шестигранный куб и на этих гранях написаны цифры 1,2,3,4.5,6. При бросании кости выпадение любой из этих очков является случайным событием. Все эти событий он считает «равновозможными».

При однократном бросании кости шанс на выпадения любого числа

16 очков можно оценить равной , т. е. вероятность выпадения шести очков равна 1 6

.

При двукратном бросании кости всех равновозможных случаев будет 36 = 6 • 6 = 6 . Из этих случаев в 11 -ти шестёрка появится хотя бы один раз и в ²⁵ = ⁵ • ⁵ = ⁵ случаях шестёрка не выпадет ни разу. Шансы на появление шестёрки хотя бы один раз будет      .

Другими словами, вероятность появления хотя бы одной шестёрки при двукратным бросании кости равна 11 36, а вероятность не появления 25 36 ни одной шестёрки будет      .

При трёхкратным бросании кости число всех возможных случаев 3

будет 216 = 6 •6 •6 = 6 , а число случаев в которых шестёрка не выпадет ни разу равна 125 = 5 ’5 •5 = 5 . А для случая четырёх костей это число будет равно 625 = 5 •5 •5 = 5 . Следовательно, что шанс на выигрыш можно оценить числом 671, а на проигрыш 625. Другими словами, вероятность того, что при четырёхкратном бросании кости появится хотя бы одна шестёрка, т.е. вероятность выигрыша игрока равна

671 1296

а

вероятность проигрыша

625 1296

Теперь можно утверждать, что вероятность выигрыша больше, чем вероятности проигрыша. Конечно, эти рассуждения привело Паскаля классическому определению вероятности. А потом можно излагать определении достоверных и невозможных событий, хотя бы например, со следующими простейшими примерами:

В урне находится десять белых шаров. Найти вероятность того, что

- P ( U ) = 10/10 = 1.

( U )

наудачу взятый шар окажется белым

А вероятность того, что этот шар окажется черным ( V ) - p ( V ) = 0/10 = 0.

И в дальнейшем можно перейти к изложению других понятий теории вероятности.

В заключении хотим отметить, то что выше было изложено, в нем нет особых открытий. Это только в некотором смысле «цитаты» из опытов авторов, хотя бы для молодых преподавателей. И здесь обратим внимание на то, что пишет Дж. Пойа о преподавании математики [6].

«Преподавание – не наука, а искусство, хоть это меньше заметно – имеет так же нечто общее с музыкой».