Приближение непрерывных функций средними Валле - Пуссена для дискретных сумм Фурье - Якоби
Автор: Коркмасов Фуад Муэддинович
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 2 т.6, 2004 года.
Бесплатный доступ
Рассмотривается система $\{P_i^{\alpha,\beta}(x)\}_{i=0}^{N-1}$ $(N=1,2,...)$ многочленов Якоби, образующих ортогональную систему на дискретном множестве $\Omega_N=\{x_1, x_2,...,x_N\}$, состоящем из нулей многочлена Якоби $P_N^{\alpha,\beta}(x)$. Для произвольной непрерывной на отрезке $[-1,1]$ функции $f(t)$ построены средние типа Валле - Пуссена $v_{m,n,N}^{\alpha,\beta}(f)=v_{m,n,N}^{\alpha,\beta}(f,t)$ для дискретных сумм Фурье - Якоби по ортонормированной системе $\{\widehat{P}_n^{\alpha,\beta}(t)= \{h_n^{\alpha,\beta}\}^{-1/2}P_n^{\alpha,\beta}(t)\}_{n=0}^{N-1}$. Доказано, что при условии $-1/2
Короткий адрес: https://sciup.org/14318110
IDR: 14318110 | УДК: 517.98
Текст научной статьи Приближение непрерывных функций средними Валле - Пуссена для дискретных сумм Фурье - Якоби
В различных прикладных и теоретических задачах широко используются разложения функций в ряды Фурье по ортонормированным системам, в частности, по ортонор-мированным многочленам (Чебышева, Якоби и др.). Нередко вместо частичной суммы ряда Фурье по выбранной ортонормированной системе в качестве аппарата приближения используются суммы (или средние) Фейера и Валле — Пуссена по той же ортонормированной системе. В современных задачах, связанных с обработкой, сжатием и передачей дискретной информации, вопросы приближения функций, заданных на дискретных множествах точек (сетках), часто решаются с помощью рядов Фурье (или их средних) по соответствующей системе ортонормированных на этих сетках многочленов. Выбор того или иного аппарата приближения продиктован стремлением обеспечить как можно лучшее приближение данной функции.
Пусть ЕР — пространство алгебраических многочленов рп = рп(ж) степени не выше п, С[—1,1] — пространство непрерывных на [—1,1] функций, Q = {жд, Ж1,... , ж„,...} — сетка — дискретное множество, состоящее из конечного или бесконечного числа различных точек действительной оси R. Обозначим через РДДД ДД > —1) классические многочлены Якоби степени N, ортогональные на отрезке [—1,1] по весу рД) = (1 — ж)“(1+ ж)/3. Теория классических ортогональных многочленов, в частности многочленов Якоби, хорошо изучена в научной литературе. Однако, как будет показано ниже, многочлены Якоби РД*3 ДР РД13 ДР..., РДДД) (N = 1,2,...) могут быть рассмотрены как многочлены, образующие ортогональную систему на сетке Q = {жд, Ж1,... , ждЦ, состоящей из нулей многочлена Якоби РД*3 ДР В этом смысле многочлены Якоби являются ортогональными многочленами дискретной переменной. Поэтому представляет интерес исследование
свойств дискретных сумм Фурве — Якоби и их линейных средних. В настоящей статье мы рассмотрим аппроксимативные свойства средних Валле — Пуссена для дискретных сумм Фурье — Якоби.
Хорошо известна следующая квадратурная формула Гаусса [1]:
1N у р(ж)сг2№-1(ж)б?ж = ^2//j справедливая для любого многочлена Ст2№-1(ж) G H2N-1. В (1) Xj = х“’3 — нули многочлена Якоби Р^’3^, щ = ц“'3 — числа Кристоффеля (или веса квадратурной формулы), и . = а+а+1Г(7У + а + 1)Г(7У + ^ + 1) 3 + 1)Г(^ + a + Р + 1) _ 2\ Г Если, В частности, ПОЛОЖИТЬ а2Л-1(ж) = Рп ’3 VxWm3 VXY т + ^ ^ 2^ — 1, то из (1) 7 cv,^ 2q+^+1 r(n+a+l)r(n+^ + l) с w ~ и - п’^\Кр0ТТ Из (3) видно, что система многочленов Якоби ^Р“’ (ж)}^1 является ортогональной на сетке CIn = {жх,Ж2, • • • ,зд}, состоящей из нулей многочлена Якоби Р^’3 (х), относительно скалярного произведения (/,д) = 52 ЛхШхШЛ W^ = g^- Полагая P“’3W = №^2P^W, (4) определим для произвольной функции /(t) G С[—1,1] дискретную частную сумму Фурье — Якоби порядка п < N — 1 по ортонормированной системе ^Р“’3W^Pq TL 8:ДП = 8Д^ = РрЙ,Рр№. № N где fk’N = 52 mHxjWk34xj^ ~ дискретные коэффициенты Фурье — Якоби. Составим средние Валле — Пуссена функции /(t) G С[—1,1]: «"Д^П = «Дли,0 - ^ \s^K(J,t) + ^11NU,<) + ... + S^+„1KU,<)], (6) где т + 71 ^ N — 1. Будем рассматривать у^п ы^Л как линейный оператор, действующий в пространстве С[—1,1], норму которого обозначим через Ци^’^ w||. В настоящей статье при условии — 1/2 < а,Р < 1/2, т < aN (0 < а < 1), 0 < bm ^ n ^ dm (а, b и d — фиксированные действительные числа) нами доказывается равномерная ограниченность в С[—1,1] нормы операторов Валле — Пуссена v^ NUY Как следствие этого результата, устанавливается порядок приближения произвольной функции /(f) е С[— 1,1] средними Валле — Пуссена ^т^л^М в пространстве С[-1,1]. 2. Вспомогательные утверждения Приведем без доказательства следующее очевидное утверждение. Лемма 1. Пусть функция f^ непрерывна, и неотрицательна на. промежутке [«i, Д] и {tj}JL0 — сетка., такая что ai < to < ti < ... < tm< bi. Пусть Mj = tj+i — tj и [«2Д2] C [cii,6i]. Тогда, 1) если f^ монотонно возрастает на. [«2,62], то б2 У f^Mj ^ I f(x)dx + f(b2)A\(7) а2<У<Ь2О2 2) если /(др монотонно убывает на [а2,62], то Ь2 У^ /(tj)Atj < [ f(x) dx + /(а2)А*, A* = maxAtj.(8) Лемма 2 [1; и. 15.3]. Если xj = cos0j (0 < 0j< л) — нули многочлена. Якоби Рф3(ж), — 1/2 < а,Р < 1/2, то для чисел Кристоффеля цу определенных равенствами (2), справедливы следующие оценки Pj ^ ^8in0jf“+1 ф<0з^л-8о^(9) /Zj < — (sin#?)2^1 (eq < 0j < тг),(10) где А и Eq — фиксированные положительные числа, j = 1, 2,... , N. Нам понадобятся некоторые свойства, многочленов Якоби [1]. Для удобства, ссылок мы соберем их в этом параграфе. Справедливо следующее равенство РфЧх) = (-Х^Рфф-хУ (И) Для —1<1<1,п>1 справедлива, следующая оценка. Нс И б > "Q"1/2< 1 > "/j"1/2 |Щ’(г)|«:ДД УГЛ+Н Л+7+1 . |12) Здесь и далее через сщс(а,/3,... , ш) обозначаются положительные постоянные, зависящие лишь от указанных параметров. Если Xj = cos0j — нули многочлена. Якоби Р^^х), —1/2 < а, р< 1/2, занумерованные в убывающем порядке: то [1] Отсюда —----тг < 93< 27 тг (; = 1,2,..., IV). 2^ + 1 7 2^ + 1 u ; ^9 = ФЧ1 - 9 > 7 Т J / О ЛГ I 1 ’ A9j < Зя 2^ + 1 Имеют место следующие равенства [2]: I. При — 1 < ж, t< 1, ж ^ t к-’Ч^=^’Ч-х^к^ = ХЛ(1Л^а+м^ i=o ' , „^WP^yto _ (4 + ЦР^ГЙЩ) - kPpWPpto 5k^ t^^X^ p^^p^ где Нгк = 0(1), 5k = 0(1) (к —> oo). В дальнейшем будем предполагать, что существуют такие положительные постоянные ср и ср, что \Нк\ < ср и \5к\ С ср - При желании значение постоянных ср и ср можно найти, используя доказательство равенства (16), приведенное в работе [2]. II. При — 1 < x,t< 1, ж ^ t I А т+п6 1 f Wz ^ kPp^WP^H^ = Е^Ж.),|17) к—тг=1 где 9At'^ = ^"^-Ж^1"^ [(т + ^ + “ + ^ + Жт^ТЧ^Рт^Ч^ _^трарН 1)Р“+1^+1(ж)Р“+1^(<)], (18) 92 И = ^7Г-^^[(т + « + ^ + 1)Р“ + 2’3№^Чх^ _^т + п + а + 3 + 2)Р“+2/(1)Р^+х(ж)] , (19) >0+1,/3 / ,\ ра^зрс , \ тРп х1)1 тРп /71 р "Г 1papij3 , . ра,[3+1 2т + а + р + 1 т V ' т (1-1)(1+ж) (а + Р + 1)(2/с + a + Р + 2) a+i/з а\ ---^ЦьТХД1?Тздй7ТХД(ТТуР‘ 1111 1211 ®(^) = MZL^T21^E^ (22> (1-^)(1+ж) V- 1 г/ , 1 \о ра+Ц(.х ^аД+Ы х а^М- ^^ Ез^ + о + л + ^ + В^-! № № k=m -аизрцр^^р^ЧкА (23) 3. Оценка норм средних Валле — Пуссена дискретных сумм Фурье — Якоби Имеет место следующая Теорема 1. Пусть —1/2 < а^р < 1/2, b,d — фиксированные положительные действительные числа, ф ^ dy Тогда, нормы средних Валле — Пуссена. г^п рДЛ при условии m < aN (0 < a< 1), 0 < bm ^ n ^ dm равномерно ограничены в пространстве С[—1,1]. < Подставляя в (6) соотношение (5) и учитывая равенства (4), (16), имеем 1 Nm+n CyUbC-NU-^ = ^t52^v(^) 52 ^а^а.(24) j=lk=m Из (24) следует справедливость равенства где ra^ _ тл0^ /д\ m,n,N v m^n^NX1) mA-п 52 к^а^а k—m Оценим величину V^’nArW при — 1 < t< 1. Рассмотрим сначала случай 0 < t< 1, который, в свою очередь, разобьем на случаи: 1) t G [0,1 — ^-], 2) t G [1 — ^, 1]. 1) Запишем нули многочлена Якоби Р^’13 ^ в убывающем порядке — 1 < xn < xn-i < ••• < xi< 1и сделаем замену t = cosy, Xj = cosOj. С учетом оценки (14) из (26) следует, что с,2л(со8^) < А0Р Положим А, - у-г), ^2 = [^ + ^¥)^3 = Р-^^+а,^ = (0^-i], Тогда величина w(cos у) оценится по следующей схеме: Clwtc08^) < ЗА тг^п + 1) I Е + Е + Е + Е ЙЩД1 0щА2 ЙЩДз УщД4 = Ur + и^ + и3 + и4. С учетом равенства (16) каждая из сумм Ui (г = 1,2,4) оценивается следующим образом: U^^U.b (29) /=о где 3N ^ (1 — cos ?)(! + cos dj) 7г(п+1) ^ j 2а+/Ах (cos р — cos v 7 ОдД, v 31 m-\-n x kPk*1,13 (cos p)Pk’/3+1 (cos dj) k—m A93. U^ = ЗА л(?г + 1) Е /^ Оща, 1 cos р — COS 03 m-\-Ti E k=m tt! p«,P nkrk+l (cosy)P“’'3 cos 63) A0,, (31) ий = ЗА л(?г + 1) Оща, 1 COS (/? — COS 63 m+n E k=m H2kPk’3 COS^P"^ cos 63) A0,, (32) игз = ЗА л(?г + 1) У,СА7 1 cos tp — cos 9j m-\-Ti E k=m HlP^P 'posp)Pk’p cos 03) A^-, (33) Ul4 = ЗА л(?г + 1) Е ^ 0,еДг 1 cos p — COS 0j m-\-TL E k=m Tj4 TDa^ HkrMA. (cos pWm\ COS 0j) A0„ (34) ^5 — ^-Z ЗА ________1________ п + !) ^ /Ъ 2“+/3+11 cos р - cos 03 \ vj Е2\г m-Vn E (fc + ^^(c08 ^^(cos e3^ k—m — 1сРа’13(сг1чтАР“,13(сг>чАЛАА ——^— и__-________ k 3 3 л(?г + 1) ^ J2“+/Ai|COS¥,-cos^ X (m + n + l)P“^n+1(cos^)P“^n+1(cos^) - mP^p(cos p)P^ (cos 03) I A93. (35) ^e = E ^ Я 77 + 1 v 7 ОщА, (1 — cos ?)(! + cos 03) x m+n 5kPk (cosp)Pk’' (cos^) ДУд k—m Для определенности в лемме 2 будем считать ед = тг/З. Поэтому на интервале Ai будем пользоваться оценкой (10), а на интервалах А2, A3, А4 — оценкой (9). Оценим Uq. При оценивании Пц (г = 0,1, 2, 3, 4, 5, 6) будем учитывать, что для 93 G Ai (sin0j)2/3+1 = (1 - cos0Д/5+1/2(1 + cos #Д/3+1/2 < 2(1 + cos9p3vP\ а также cos ср — cos Oj ^ 1/2, (1 — cos ОД “l"2, х/4 < 1 и (1 + cos у) № V4 ^ 1. Принимая во внимание (10), (12), (30)—(34) при т Д aN (0 < а < 1), 0 < bm Д n Д dm имеем 77ю ^ 6Ас2(а, /3) тг(п + 1) £ (8т0Д2^хД0,- Oj-eAi 6Ас2 (а, /3) тг(п + 1) У А^- < 2Ас2 («,£), Oj-eAi Um < 1 \ 2 / о\ (^З'+та -1 \ !2АС КД) _ /2_1/4 у (1 ^ayWiH у 1 Ду тгп+1 ^ 3’ Х^к 3 12Ас2(а,/3) /9 , 9, < -----A2AEQim«+4/2 \ Д6>74Aq4c2 аД лт z—‘ 03EN\ Величины 1712, П1з, 1714 оцениваются аналогично 77ц. Поэтому Иц< 4Ащс2(а,/3) (/ = 2,3,4). Далее, из (35) и (36) с учетом (10) и (12) выводим 12Ас2 6,gAi 12Ас2 Oj-eAi ««H^HN^i-^-niwi! У (™ед«+> л п + 1 z—' КД1 тД-тг к—т 6Ас2(а, /3) ------------92 лт Е о,еА1 NOj< 2А92с2(а,/3). Объединяя оценки (37)-(41) и сравнивая их с (29), получим 771 < 2Ас2(а,/3) Оценим величину 772. Для этого используем без доказательства следующее Утверждение 1. Если т < aN (0 < а < 1), 0 < bm< n < dm, то Esin 0 j (cos — cos On) -q/2+5/4 «ща2x f n Зла, _«>i/9 < у 2 (сДа) + —(тг + 1) ) т , У ___Д0 (cos to — cos On)2 3*2 9jEA2 V3 1 4--(л + 1) 771(1 — COS to) ' , 4 ') E Sin V-i 7Г / , . oTTCL , . \ _ а I 3 3 ----------------—-Д^- ^ — I c2(a) 4--— (л + 1)1т з+ i (1 — cos 0,eA2(с°8У-со8 0Д-2+т 4 у Е о,еД2 sin Oj cos ср — COS Oj . . _ , 3% о Зла, . △0; < In—m 4--— 7Г + 1 . 3 8 4 При оценивании IE, (г = 0,1, 2, 3, 4, 5, 6) учтем, что для Oj G Д2 (1 + cos^j) /j/2 4/4< V2, (1 + cos 0j)—^/2+4/4< V2, (sin0j)2a+1 = (1 — cos0j)“(l + cos0j)a sin#j < V2(l — cos^)“ sin0j, а также (1 + cos -/j/2-1/4< 1. Из (31), с учетом (9), (12) и (43), имеем Аналогично, ^ЗД2А H2i < с2(а,/?)—^91 V7Г Зла "Т" U2i< с2(а,/?) З^А Зла (г = 2,3,4). Оценивание величин U25 и U26 аналогично оцениванию U21. Действительно, из (35), (36) с учетом (9), (12) и (43), имеем U25 < 6Ас2(а, 3) л(п + 1) (l-cosy?) Q/2 4/4 Е ^ЕДг ________________7___________Д у . (cos <р — COS 0Д-“/2+5/4 3 П26 < 6Ас2(а, 3) л(п + 1) С2(а, 7) ЗуДА V^b Зтга "Т" 92 (1 - COS v)-o/2+l/« £ 0jeA2 . п /т+п 1 (cos го — cos 0, )-а/2+5/4 \, к J \к=т с2(а, /3) ЗУ2А —^92 сх(а) + —-—(тг + Наконец, перейдем к оцениванию величины U20. С учетом (9) и (17) из (30) имеем U20 ^ п 52 (8т0Д2а+152|дг(со8(р,со80Д|А^ = ^и^, ’ 9jEA2 г=1 г=1 где (sin0j)2a+1 gz(cos ср, cos Oj)\AOj (г = 1, 2, 3, 4, 5, 6). 0j-eA2 7г(?г + 1) Оценим H^’. Используя (12) и (18), получим (1) ЗАсДаД 20 7Г(П + 1) (l-cos^)-“/2+1/4 V sing^-^^^^A^. J cos to - COS 0i 2 J OjEA-2 v v 31 Воспользовавшись неравенством (1 - cos0j)“/2+1/4 < (1 - cos и оценками (44) и (45) из (53), получим 21 Ас2 (а,/3) i/2 ' sin У, —, v V. (1 - cosy)1/2 > ----------3n x9 Л 77 + 1 -^ COSy — COStC2 03ех-2Х v 31 21Ac2(a,^) os а/2+1/4 у ______________________________________J. (cos у — COS 0Д”а/2 + 7/4 3 Л 77 + 1 Z—' Cca2 21Ac2(a, [3^ 1 + c2(a) 4--— (л + 1) Далее, принимая во внимание оценки (12), (44), (46), равенства (19)—(23), из (52) имеем ту U20 21Ac2(a, /3) л(?7 + 1) (1 - cosy)1/2 ^2 СеДг sin Oj (cos у — COS Д)2 21Ac2(a,/3) Ai Зла A 1 + —77 + 1 • A 4 / y(3) у 12Ac2(a,^) ^—^ sin Д 20 лт(т7+1) -^ (cos у — cos Д)2 v ' Oj ex-2 v v 31 3Ac2(a, /3) А, Зла A 1 + —у 77 + 1 • A 4 / U^ U20 6Ac2(a,/3) л Л Зтга, , 1/9 3Ac2(a,/3) / Зтга, X ---' Д 1 + ~T^ + 11- cosy)"1/2< ---1 + — л + 1 . л?77 2 \ 4 ) 2 у 4 / U^ U20 9Ac2(a,/3) v^ sin07 9Ac2(a,/3) Al , Зл 2 Зла, 1XA < ----—X± \ -------I---дд. ^ ----L_12. _ in —m2 _|--(тг + I) ТГ777 z-^‘ cos у — cos Oj TT A m 8 4m / 0aex-2 x / < 9Ac2 (a, /3)7(777), где 7(777) = — In ^m2 + -^-(тг + I). ' v / 7rm 8 4m v / Нетрудно видеть, что 7(777) = 2 In 3a 2 2 За, 1 х 4 За, 1 х — •--1--(л + 1) ^ — • —I л + 1) ^ 1--л + 1). Л 777 4 777 1 л 5 4 ' 5л 4 ' Поэтому U^<9Ac2(a,/l) fA + ^r(Tr+l)Y (59) 2U А 5тг 4 / Далее, ^(6) U20 £^W) v- __^__Д. < ЭАсДаД 2тГ7772 -^ (cos у — cos 07)2 17 8 0aex-2 1 АА Зтга A 1 + —77 + 1 A 4 у Собирая оценки (55)—(60) и сравнивая с (51), заключаем, что U20 < ЗХсЧа,^ fl ++ 1)) А о о у аУ 7 А / х Зтга, 1ХА 12 9а, 1Х1,„ + Т7 с2(а) + —(л+!) + —+ —(уг + !) . (61) 26 А 4 у 5л4 Из (29) и (47)—(50), (61) выводим U2< ЗАЯ1(а,а,6)с2(а,/3), где 8 7 Ь + 8 П \ (а, а, Ь) — \ I щ (а) Н---— (я + 1)1 I 4qi + q2 + у ) + V 7Г \ 4 / \о/ Д Зтга, \ 7 / . . Зтга, А 12 9a,_ х 1 Н--— тг + 1 + — с2 а Н--— тг + 1 + ---h —(тг + 1 .63 \ 4 У 26 \ 4 У 5тг4 Оценим величину Щ. Приведем без доказательства следующее Утверждение 2. Если т ^ aN (0 < а < 1), 0 < Ьт ^ n ^ dm, то Е 0ЩД4 sin Д(1 — cosy?) 72-1/4 (l-cos^)"/2 1/4 COS 0j — cos ip 3 Esin 0; -------------у A (cos 0. — COS to)2 0ЩД4 V 3 ___ /1 _ дда/2+1/4 v a у 1 COS vg у ■^ (cos 04 — COS to)2 ДД4 v 3 тг2 / Зтг2а У (1 + ~ 16(3-2a)“"3/2 16 Y Принимая во внимание, что для 0j G Д4 (l + cos^) 2 4 ^ 1, (l + cos^) з + 4 ^ ^/2, (sin0j)2a+1 = (1 — cos0j)“(l + cos0j)a sin#j < \/2(l — cos0j)a sin#?, (8т^)2а+1 = (1 -cos^)a+1/2(l + cos^)a+1/2 < 2(1 - cos^)a+1/2, а также (1 + cosy?) /j/2 x/4 < 1, из (31) с учетом (9), (12), (66) получим П41 < Sy^A^ta,^) я(п + 1) У^ sin0j(1 — cosy?) 2 4 Ощд4 . . a__1 ( 1 — COS 0j ) 2 4 COS 0j — cos y? ЗС2Ащс2(а,/3) Гл Зла ( тг2v^\ 1 < ------------- - + С1(а)(тг + 1) + — I 1 + ^p I .(67) Совершенно аналогично можно доказать, что 3\/2Ас/1С2(а,/3) л Зла Л л2х/^\ Um < -----------— — + ci(a)(y + 1) Н--^13--7— (г = 2,3,4).(68) я 3 у2 \4 Далее, из (35) и (36), с учетом (9), (12) и (64), имеем ^|АД1 у ^ел-С08т"'’--и^^ я(п + 1) ^ 3 cos Д —cosy? v 7 СеД-1 3V2Ac2( xb Л Зла / л2 \/2 )| TT , 6Aq2c2 a,/? 1/2 a l-cosy /2 a \«/2-i/4 ^46 < ----- ' 1 - COS to Z > sm07--------^--------- l-COS07 a/ Z л п + l ^ 3 cos 07-COS to V 7 0,GA4 3 v 'т-\-ть 6Ac/2C2(a, /3) k—m Л Зтгa / тг2\/2 )| Перейдем к оценке величины Hjq. Из (30), учитывая (9) и (17)—(23), имеем ЗА П40 ^ -;—7 0,GA4 где Аб _ ЗА 40 — , 2a+1 |gz(cos 07еА4 Величины Щд оцениваем так же, как Щд , используя вместо оценок (44)-(46) (64)-(66): оценки (i) 3Ac2 u40 ^ /2 + 1/4 (!~ COS ^)а/2 + 1/4Д6, (cos Oj — COS ф)2 3 21 Ас2 sin 9j 21 Ac2 ■^ (cos Ox — cos to)2 07GA4V 3 л / Зл2аА 2 (1 + ~)’ A^- rr(2) / 3V2Ac2(a,^) ( 5 < ПДхДа ^ „+31,_ у (1 — COS 0j)“/2 + 1/4 21V2Ac2 xb 07GA4 (2q + 1)“+1/2 ^ (cos 0i — COS to)2 y,GA4v 3 (1 — COS 07)a/2+1/4 —7 a П-^^ (cos Oj — cos 3л1 a 16(3 - 2a)Q"3/2 16 6^2 Ac2 12Д2ХсДа,р) / (2a + l)Q+1/2 х-а/2 + 1/4 1 - COS0J “/2 + 1/4 (l-cos a!2*vH X 1-----—a--- (cos У7 — COS to)2 0,GA4 v 3 Зл'а\ 16 V A^- A^- 6V2Ac2( xb 16(3 - 2a)Q"3/2 (2q+ 1)“+1/2 3л1 a 16(3 - 2a)a"3/2 16 6д/2Ас2(а,^) CoGy)-“/2+1/4 V ^ ~ cosgj)a/2+1/4 тг(п + 1) -^ (cos Oj — COS y?)2 \ ■^ v ' C’GA4 j \k=m бУ2Ас2(< ТГ7712 Cga4 (1 - COS0,)“/2+1/4 Л A _( Д 12 ^®j (COS Oj — cos Зу^Ас2 ТГ 16(3 - 2a)Q-3/2 Зтг1 а 9Ас2(а,^) ' . „ , . ——----—-(1 —cosy?) ' 2 v sin Oj (1 — cosy?) /2 — 1 /4 U—СО^)"/^^ m-Vn k—m Cga4 9Ас2(а, ТГ COS Oj — cos у? 9Ac2 (1-cosy?) q/2+1/4 ЭАс^а^ (2а + 1)а+1/2 \/2тгт у 16(3 — 2а)“-3/2 9Ас2(а,/3) / (2а + 1)“+1/2 2^тг I 16(3-2а)“-3/2 ТГ Cga4 Зтг' a Зтг1 а Зтга ( тг2\/2 (l-cos0,r/2+1/4r^ (cos 0j — COS y?)2y^T1 V 1 , (91) Собирая оценки (73)—(78) и подставляя их в (71), получим П40 < ЗАс2(а,/3) 7тг2 Л Зтг2аА / 9\/2 7 ТГ 2^2 Зтг1 а 9тга ( тг2\/2 , (79) Из (67)—(70), (79) имеем U4< ЗАК2(а, а, 6)с2 (а,/5), где ТГ 7тг2 IT 9^2 7 b 2^2 Зтг1 а ТГ Зтга V2 ))| • (81) Оценим величину Щ. Из (28), учитывая оценки (9) и (16), имеем ЗА Се Аз m+n к к=т г=0 = —----ту Е (sni3y2n'’АД i^o’E' ~ ---— ^ (sinfy)2"41 ' ' 03Е^а k=m х ' 03Е^а т+n к X Е E^K'lC^cosy,)! • l^costyA^ = 1/У + и^.(82) к=т г=1 Оценим сумму U^V Учитывая, что для — 1/2 < а, 3< 1/2 (см. (3)) «,/31-1 _ а + /? + 1 Г(а + /3 + 1) _ _____Г(а + ^ + 2) 0 1 “ 2“+/j+1 ' rfa + lirt/S + l) ” 2а+/^+1Г(а + 1)Г(/3 + 1) [Г(1,462)]2’ получаем 7.68А 7г(п + 1) J2 (sinfy)20^^ < + еД3 — V АО 7Г ^^ ^■еДз 15.36А 7Г Для оценки U^ нам понадобится следующее Утверждение 3 [3]. При фиксированном р имеет место равенство Г(У+ р) IW) = ж 1 + 0 1 А УД N -д оо, основанное на. хорошо известной формуле Стирлинга. В силу этого утверждения, величина {/t“’/j}-1 имеет порядок О (г) или {/i“’/j}-1 ^ cyl. Учитывая, что для Oj G Аз (1 + cos 0Д+4/2-1/4< \/2, (8т0Д2а+1 = (1 — cos ^Д а^4^2 (1 + со8 0Да+4/2 < ^(1 — со8 0Да+4/2 И (1 + COS у?) Ж Х/4 ^ 1, из (82) получаем ^з 6Ас4С2(а, /3) л(?г + 1) m-Vn к Е Е^1 - «w)““/2“x/4 е i1 - к-m г=1 ^бДз СО8 0Да/2 + Х/4Д^ / 1\\«/2 + 1/4 1 — cos -- \ m / / / / 1А / 1АА“/2+х/412 12Ас4с2(а,/3) + cos <р--— cos I у Н-- — < ---------—— у у m) у mJ / J m лтдз + 1) т+п к xEEU-co^)^4 к=т г=1 тщсДа^уд х лт(п + 1) -^ 2 к=т г л 1AV 4L 1 — cos у?-- + 2 sin ip sin — у т// у ту 12Ас4С2(а, /3) лт^п + 1) m-Vn к к=т г=1 23/4т 2 4 (1 — cos у?) ~+s 12(1 + 2т)Ас4с2(а,/3) у^Л лтН + 1) -А^ -А^ к=т г=1 12 1 + 23/4 Ас4с2 М z w 12(1 + 23/4)A(d + 1)с4 2 <— ------1—\ ' (т + 71 71 + 1 < — ------—----—с2 а,/3 .85 лт(п + 1) v м 7 л 77 Объединяя (83), (85), получим Щ ^ Д±аД [12(1 + 2а^с4сЧ«, /3)] + Д|Д.(86) Собирая оценки (42), (62), (80), (86) и сопоставляя их с (28), при —1/2 < a, Р< 1/2, in < aN (0 < а < 1), 0 < bm ^ n ^ dm приходим к оценке < Xc2(a,P)H3(a,a,b,d) + -15.36 ( 0 < 1 < 1 - ,(87) где / 2 А 12(1+ 23/4) Н3^а, а,Ь^ = 2 8q4 + 92 + —Ь 1 ) + ЗН4^а, а, 6) + 3H2^ct, а, 6) +-----------c4^d + 1), I88) а Hi\a,a,b^ и Н2^а,а,Ь^ определяются из соотношений (63) и (81). 2) Неравенство (27) запишем в следующем виде: где омм N т+п КДл (cos у) < , п X ^3 > .Kk (C0S У’ cos 63^ k=m 3N 7Г(Т1 + 1) ЙЩД1 ЙЩД2 с с Аз Mj △1 Л2 = Л 8 \ 2л arccos 1--т , — \ т2) 3 Аз = 0, arccos а суммы Ж Р = 1,2) оцениваются с помощью равенства (16) аналогично суммам Up. (Суммы Ж/ имеют тот же смысл, что и Up. Поэтому всюду далее при оценке Ж/ будем пользоваться равенствами (30)-(36)). При оценивании величин Ж и Ж вместо оценки (см. (12)) \Pk’PW\< с(а,/З)^-1/2(1 - Ж“/2"1/4 следует воспользоваться оценкой \Р“’!3 (1) | < с(а, р>а (1 - 4/?112< 1 < 1) . Оценим величину Ж- Учитывая, что для 63 G Ai выполняются неравенства cosy? — cos^j > 1/2, (1 — cos0j)-a/2-1/4< 1, (sin0j)2/3+1 = (1 - cos0j)/3+1/2(l + cos93p3^!2< 2(1 + cos0j)/3+1/2 и используя равенство (16) и оценки (10), (12), (91), получим (1 — 4/m2 Д cosy? Д 1) Wio ^ 16A(ri +IJ^fa,^),(92) ТУп 54 8Ащс2(а,Я(93) Аналогично можно показать, что Wti < SAqic2^,^ (г = 2,3,4).(94) Далее / 4A(d + 3) 2//пг\ Жб < —^---с (а,/?),(95) Же < 16A(d + 1у12сЧ«,РУ(96) Собирая оценки (92)—(96) и подставляя их в (90), выводим ИА < IGAcfa,^) 2 Для оценки W2i (^ = 1,6) укажем без доказательства следующее Утверждение 4. Если т Д aN (0 < а < 1), 0 < Ьт ^ n ^ dm, то V ____^____Аб. m"^. ~- (cosy? - cos07)"а/2+5/4 йща2 Для ИА1 с учетом оценок (9) и (98) имеем (8т0Д2а< ^(1 - со80Да, (IAgos^/2-1/4< V2, (l + cos^)"^1/4< V2 ^21 ^ l^lc2(a^)mQ-l/2 у ------ Я (cos у? — COS 0,)-а/2 + 5/4 Сед2 12Ащ / Зла А 2 А ---- сДа) 4--— с ta,p). л у2 / Аналогично доказывается, что ИА, Д ^^ ^с,(«) + ^^^(ск/А) Д = 2,3,4).(100) л \/ Далее, используя равенства (35), (36) и оценки (9), (98), получим 1^25 < 6А(с? + 3)с2 «)та + 1/2 у- _______^2 7г(п+1) ’ ^—у_ фо%Д) — СО%9Л-а^^Ъ^ 6A(d + 3) / . х ЗлаА 2/ —Н-- сДа) + — с2<а,^ ЛО \2 / и 1^26 ^ 48А92С2(а,^) +1/2 у. _______у£,________ лт2 ^—4. (cos у? — cos 0j)-a/2+5/4 ДСД2 48A(tZ + 1)^2 л Наконец, оценим И^о- Для этого приведем без доказательства Утверждение 5. Если т < aN (0 < а < 1), 0 < bm ^ n ^ dm, то Esin _ т2 _ (cos у — cos 07 )2 7'1 07еА2 (ЮЗ) х - sin бз л _ m a+3/2 ~- (cosy - cos07)-a/2+7/4 7 2 CeA2 E CeA2 sm07 . „ , , 3 9 Зяа --------3-----A07< In -m2 4--. cos у — cos Oj 8 2 (Ю4) (Ю5) Величину ИДо оценим тем же способом, что U^o, везде используя оценку (91), а вместо оценок (44)-(46) — оценки (102)—(104). В конечном итоге, получается ИДо ^ ЗХТЩа, a,b, d)c2 (а, /3), (Юб) где Щ^а, a, b, d') = -------- 1 + 02(a) 4--— яо у 2 / + 1 Л +(I+ i2(d + 1) + | U^d + 4)3/2 + (d + 2)) - + 1)) . (107) я \ 2 / \ 2 b \ / 5я / Собирая оценки (99)—(102), (106), получим И^2 ^ ХН$(а, a,b, d)c2(a, /3), где Н^а, a,b,d) = — (ci (а) 4( 8(qi + (d + 1)92) 4) + З-НДа, a, b, d?). (109) я X 2 / X о ) Оценим величину W3. Из (89), с учетом (9), (16) и (91), имеем „, m+n к Ws ^ ДДП) («т0Д2а+1 £ £{/z^}"1|^(cosy)| • |^^(со80Д|Д^ 7 0,еАз к=т i=0 Q \ ТП-^ТЬ = -,---77 У (sinfl/^A^ VVio'3V + -,---77 У (8тУД2а+1(110) я п+1 ^ v 3 ^ 1 0 J я п+1 ^ v 31v 7 03E^s k=m 0aEA3 тД-тг к X £ У^УУК’Чсоб^ . l^’^cos^JIA^- = w3(1) + wf Величина иУ оценивается аналогично Пд1^ (см. (83)): У1’ < 7.68А я(п + 1) У (8т0Д2а+1 0з е д з тД-ть \ Е1 д^ < к-m / 7.68А я У (8т0Д2а+1А^ (Ш) 7.68А / 8 А ----- arccos 1 --т я \ mz j 7.68А я 2я — < 15.36А. т Как было показано при оценке величины Щ , в силу утверждения 3 величина Vi"’13^”1 ^ СП- Кроме того, для 9j е Аз (1 + cos У^)-^/2-1/4< 1 и (sin^)2а+1/2< ^(1 — COS 0j)“ + 1/2. Поэтому (2) 3V2Ac^) у cos0 ^/з+П4 f V ^+3/2^j А93 OjE^x k—m Зу^Ас^а,^) ----7---~77---с4 24(d + 2)2Ас4с2(а, 3) 2тг 2 2 —-------- ' т—< 24(d + 2)2Ас4с2(а,/3). 7Г т Окончателвно из (110)-(112) W3< 24(d + 2)2Xc4c2(a,3) + 15.36А. (ИЗ) Объединяя оценки (97), (108), (ИЗ) и сопоставляя их с (89), получаем при —1/2 < а,3 < 1/2, 77i < aN (0 < а < 1), 0 < Ьт < n < dm V^LnW < Xc2(a,p)H^a,a,b,d) + 15.36А где Н^а, a, b, d^ = 16 2fli + (fl2 + !)((/+ 1) Н---^- + Нб^а, a, b, d) + 24(с? + 2)2с4. (И5) Из (87) и (114), в свою очередь, выводим при —1/2 < а,3 < 1/2, т ^ aN (0 < а < 1), 0 < Ьт ^ 77 ^ dm V“’^N^ < Лс2(“’ ^НЛ<Н a, b, d) + ^^15.36А (0 < t< 1), (116) где Нт^а, a, b, d) = Н3(а, a, b, d) + H^ct, a, b, dY Перейдем теперь к случаю — 1 ^ t ^ 0. Его с помощью равенства (11) легко можно свести к уже рассмотренному случаю 0 ^ 1 ^ 1. В итоге получим при —1/2 < а, Р < 1/2, т ^ aN (0 < а < 1), 0 < Ьт ^ 77 ^ dm CInW < Xc2^,p^H8^,a,b,d^ + 1±115.36А (-1 < t< 0), где величина Н§ф, a, b, d^) получается из 7?т(а, a, b, d^) заменой а на /3 во всех постоянных, входящих в Нт^а, a, b, dy Сопоставляя (116), (117) с (26) и (25), выводим, что при —1/2 <а,Р < 1/2, 777 < aN (0 < а < 1), 0 < Ьт ^ 77 ^ dm Vm,n,NW ^ Xc2(a,p)H(a,p,a,b,d') + ^1зО.72А (-1 < t< 1), где Ща, 3, a, b, d') = Нт^а, a, b, d') + Нйф, a, b,dy > 4. Приближение непрерывных функций средними Валле — Пуссена Пусть /(t) G С[—1,1], p^W Е Нт — многочлен наилучшего приближения функции /(f) в пространстве С[—1,1]. Обозначим через Em(f) = max /(f) — p„№\ ~ наилучшее приближение функции /(f) алгебраическими многочленами степени т. Имеет место следующая Теорема 2. Если № е С|-1 1], ^Uy-ti^U, 0 - средние Валле - Пуссена дискретных сумм Фурье — Якоби, то при —1/2 < а,3< 1/2, m ^ aN (0 < а < 1), О < bm< n < dm, m + n ^ N — 1 ^N^Wlt^cE^fY где с — некоторая положительная постоянная, зависящая от a, 3, a, b, d. < Заметим, что из (5), (6) следует, что средние Валле — Пуссена С^1^ КШне изменяют алгебраического многочлена pm G Нт, т. е. N(pm,t) = N(pmy Используя соотношения (24), (26) и (133), имеем К".»(/, о-/(<)! < y^yM-Pm№ + K„w-fW\ < 41Л р;д 1МКД.МДД11Ы1; = (1 + Н(а, 3, a, b, d))Em(t) < cEm(t). > Таким образом, средние Валле — Пуссена ’’'‘"'„уЗ-б дискретных сумм Фурье — Якоби приближают непрерывную функцию (при наличии лишь информации о значениях этой функции в конечном числе точек Qw Е [—1,1]) со скоростью наилучшего приближения £„313 этой функции среди алгебраических многочленов степени т.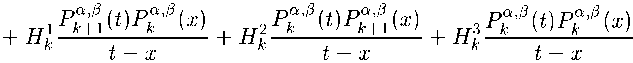
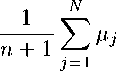
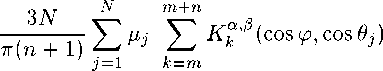
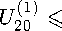
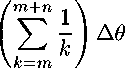
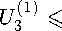
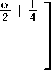

I
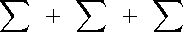
= ж + 1H2 + ж,
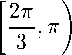
6 ж < 52 Ж/. /=1
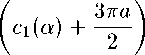
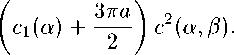
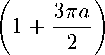
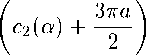
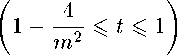
Список литературы Приближение непрерывных функций средними Валле - Пуссена для дискретных сумм Фурье - Якоби
- Сегё Г. Ортогональные многочлены.-М.: Физматгиз, 1962.
- Шарапудинов И. И., Вагабов И. А. О сходимости средних Валле -Пуссена для сумм Фурье -Якоби//Мат. заметки.-1996.-Т. 60, вып. 4.-С. 569-586.
- Суетин П. К. Классические ортогональные многочлены.-М.: Наука, 1976.


