Приближенное решение дифференциальных уравнений с отражением аргумента
Автор: Рекка Римма Александровна, Скачкова Елена Александровна
Журнал: Вестник Пермского университета. Серия: Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Математика
Статья в выпуске: 3 (11), 2012 года.
Бесплатный доступ
Рассматривается применение метода осциллирующих функций к нахождению приближенного решения задачи Коши для дифференциального уравнения с отражением аргумента; получены оценки погрешности построенного решения.
Дифференциальное уравнение с отражением аргумента, метод осциллирующих функций, лирующих функций
Короткий адрес: https://sciup.org/14729800
IDR: 14729800
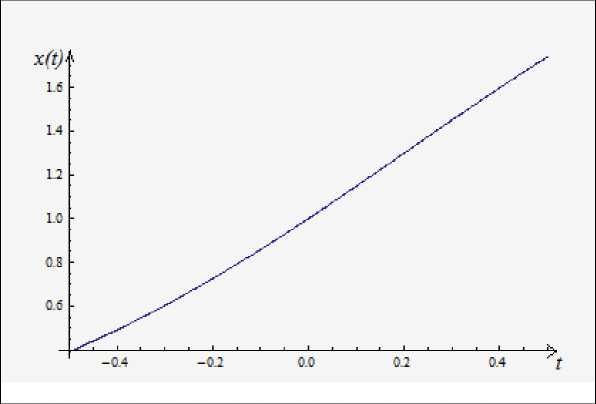
Список литературы Приближенное решение дифференциальных уравнений с отражением аргумента
- Aftabizateh A.R., Huang Y.K. Bounded solutions for differential equations with reflection of the argument//J. Math. Anal. and Appl. 1988. Vol. 135.
- Ма T.F., Miranda E.S., De Souza Cortes M.B. A nonlinear differential equation involving reflection of the argument//Archivum Mathematicum (BRNO). 2004.T. 40.
- Ведь Ю.А., Матраимов М.Т. Вопросы корректности, ограниченности и стабилизации решения задачи Коши для дифференциальных уравнений с отражением аргумента//Исследования по интегродифференциальным уравнениям. Фрунзе: Илим, 1989. С.73-85.
- Матраимов М.Т. О существовании ограниченного решения систем дифференциальных уравнений с отражением аргумента//Исследования по интегродифференциальным уравнениям. Фрунзе: Илим, 1989. С.86-90.
- Воронина Н.В., Маланин В.В., Рекка Р.А. Осциллирующие функции и некоторые их приложения. Свердловск: Изд-во Урал. унта, 1990. 111с.
Статья научная
