Приближенное решение для мод изогнутого оптического волокна

прямой волоконный световод с некоторым эквивалентным профилем показателя преломления, для которого задачу решают хорошо известным методом приближения Гаусса [21–23]. Как и в [24] метод приближения Гаусса применяли совместно с методом стратификации [25; 26], что позволило получить аналитическое решение для волокна с произвольным профилем показателя преломления и моды произвольного порядка. Однако, представленные в [20] аналитические выражения для постоянной распространения и характеристическое уравнение справедливы лишь для кусочнорегулярной модели изогнутого волоконного световода, что вносит дополнительную погрешность. Кроме того, в качестве примера выбран «плохой» профиль показателя преломления, который не типичен для современных оптических волокон. В данной работе, предлагается решение для произвольной моды изогнутого оптического волокна с произвольным профилем показателя преломления, базирующееся на изложенном в [20] подходе, но свободное от указанных выше недостатков.

Как было отмечено выше, для определения параметров моды радиального порядка m и азимутального порядка l многомодового оптического волокна воспользу емся мет одом приближения

LM^^e © Бурдин В.А. и др., 2019

Гаусса, согласно которому в общем случае для оптического волокна с профилем показателя преломления, описываемому зависимостью n ( r , ф ),

^{ev                   r}C       J

выражение для постоянной распространения имеет вид [23; 24]:

Р2 =

--------------------------х да 2п

х

^ да 2 п

V 0 0

да 2 n

-

^да ^ⁿ l 72                      7

Jjk F2m ( х )+ ТЛ’ ( X )

cos2

Здесь

F l²m ( ^X ) = ^{xl L}m - 1 ( ^X ) exP ( ^{- X} ) ,

X = R 2/ R 0 ,

Следует отметить, что в ряде работ рекомендуют в формуле (3) вместо значения радиуса изгиба подставлять некоторое эквивалентное значение. Так, в [7] предлагается использовать значение эквивалентного радиуса изгиба равное r Ce = 1,28 r C , а в [9] равное r Ce = 1,40 r C .

Поскольку r C >>  a , то из (5) следует

)

J

n e ²

F_{l , m} ²( x ) – радиальное распределение поля моды LP m ; r , ф , z — координаты цилиндрической системы координат ( r - радиальная, ф - азимутальная);

a – радиус сердцевины световода; r ₀ – эквивалентный радиус поля моды; R = r / a - нормированная радиальная координата; R о = r ₀ / a - нормированный эквивалентный радиус поля моды; L_m ^{( l )}( x ) – полином Лагерра; k = 2 п / X - постоянная распространения свободного пространства; X - длина

волны.

Интегрируя, из (1) получаем [24]:

„     (m -1)!

(m +I -1)!

{ да 2 n

^П 0 0

C1m =

m (m +I -1)! (m +I -1)( m +I - 2)!

+

i = 0

i !

.

Как и в [20] будем рассматривать изогнутый волоконный световод, радиус кривизны которого r_C значительно превышает диаметр сердцевины. В этом случае изогнутый световод может быть заменен некоторым прямым (не изогнутым) световодом с эквивалентным профилем показателя преломления, определяемым формулой [1; 2]:

Подставляя (6) в (3), получаем

| да

2_ ⁽ m 1 ) ! I 2 Г 2 2      2

I 0

х

2 п

J e2r соз(ф)/;

L 0                         J

Известно, что [27; 28]

П

.

где p – целое число; I_p ( b ) – модифицированная функция Бесселя первого рода целого порядка от аргумента b.

Учитывая, что подынтегральная функция в (7) является четной, согласно (8)–(9) из (7) получаем:

R 2_ _( m _j)!_ ^{1 4 да}_k 2 2     2

.

Здесь n = 2 r ₀ / r C .

Как и в [24] стратифицируем сердцевину световода и полагаем его оболочку однородной и бесконечной. В результате получаем:

-

х

N

2 Е ^{k 2 А П} 2 ^Ф 1 , m ( ^Xi , n )

C l , m a ² R ₀ ²

,

да .

x

J

G l,m ( x , n ) = J F 1 , m ( y ) I 2 1 ( n T y ) dy , x

A n² = n^{2 -} n² + i , n i = n ⁽ r i ).

Здесь N – число слоев в сердцевине.

Для вычисления интеграла (11) воспользуемся разложением модифицированной функции Бесселя целого порядка в ряд [27; 28]:

= _E(ⁿ2)y _x u = 0 ^{u ! ( 2 1 + u} ) ^!

2( m-1) j x E gp J yu+p+21exp (-y) dy.

p = 0      x

Интеграл в (18), (20) является табличным и вычисляется по формуле [27–29]:

f z X 2 1 » ( z 2 /4 ) u

I21 (z ^[jJ Eu,(2Z + u)1 uu u=0

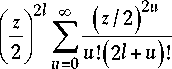
J                         n

J y n exp (^- y ) dy = exp (^- y )E/ ⁿ".\, y n ^- i .          ⁽²¹⁾

_x                                   i = 0 ⁽ n ^- i ) •

Или в более удобном для дальнейших операций

виде

Согласно (21) после группирования членов сумм из (19), (20) получаем следующие аналитические

1 0 ( z ^ u = 0

,2 u + 2 1

, - ₂, ( z )                              .

² ' ”  ^E„ u ! ( ^{2 1} + u ) !

выражения для вычисления искомых интегральных функций:

Подставляя (14) в (13) получаем следующее выражение для искомой интегральной функции:

У-EV; J yu FF2m (y) dy,(15)

u=0

_m J ( _n /2 ) ^{2 ( u + 1} ) J

Gm(x, n)=E,J yu+Fmm(y) dy.

0 uu

x

G ,⁽⁰ ) ( x ,n) =

, m , ¹

J

=exp (-x )E u=0

V = u + p + 1 ,

G 1 , m ( ^x , n ) =

(n'2)2u УУ  viZ-t u•u• E Egp (v - i)!,

Представим произведение полиномов Лагерра в виде ряда [27; 28]:

^J     /2)²⁽ u ^{+ 1 ) 2 ( m 1 ) v}         v - - i

= exp( - x )EyLF E E .

u=0 u •(21 + u ) • p=0 i=0     ( V i) • v = u + p + 21.

m ₁ + m ₂

L( 11) (x) L12) (x) = У gx^, m1m2             p p=0

min p,m g_ =      У 2' q(12) q(1),

° p        Д^ j,,m2 p-j,m j=max(0, p - m 1)

Поскольку n <<  1 то, несмотря на бесконечный предел, ряд по u в (20) сходится достаточно быстро.

Дифференцируя выражение (11) для квадрата постоянной распространения моды в по R 0

и приравнивая полученную производную нулю

( др ² / д R 0 = 0), получаем характеристическое урав-

нение относительно эквивалентного радиуса пят-

q (1) =      (к + mi)• qj,mi    j•(mi - j)•(1i + j)!.

на моды R ₀ :

Подставляя (17) в (2) получаем

2 ( m - 1 )

F²m ( x ) = exp ( ^- x ) E g p x ^{p + 1} .                    ⁽¹⁸⁾

p = 0

N

2 У к ² A n ² r ²

ii i=1

[ F 1 , m ( r i²/ r 0 ² )П - C 1 , m = °.

F 1 , m ( ^x ) = F 1²m ( ^x ) ^[ I 0 ( nV x ) ⁺ I 2 1 ( nV x ) ] .

После подстановки (18) в (15) и (16) приходим к следующим выражениям для искомой интегральной функции:

G ,⁽0) ( x , n) =

, m ,

»(V2)^{2 u 2 (} m - ^{1 ) J}                             (¹⁹)

=E^uy E gp JyU+p +exp(-y)dy, u=0          p=0    x

G ,^{( 1 )} (x , n) =

, m    , ¹

В результате получили в замкнутом виде приближенное аналитическое решение для произвольной моды изогнутого круглого слабонаправляющего волоконного световода с произвольным профилем показателя преломления. Решая характеристическое уравнение (24), определяем эквивалентный радиус пятна моды, зная который по формуле (11) с учетом (12) и (22), (23) рассчитываем постоянную распространения моды. Определив эквивалентный радиус пятна моды Лагерра – Гаусса можно найти и остальные ее параметры.

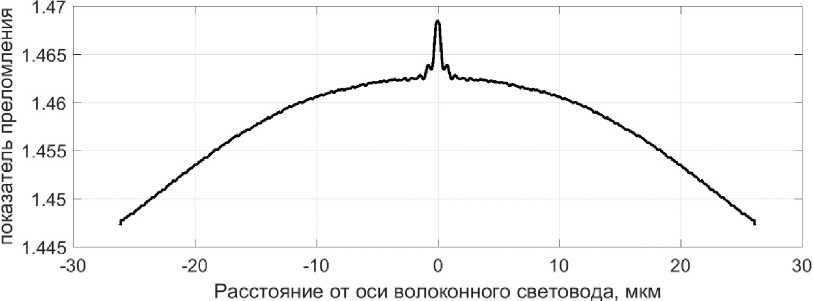
Рис. 1. Пример профиля показателя преломления многомодового оптического волокна 50/125

2a/Rc

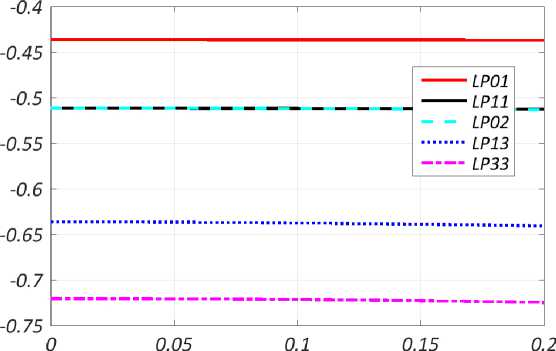
Рис. 2. Зависимости от радиуса изгиба расхождения оценок постоянных распространения мод прямого и изогнутого оптического волокна

В качестве примера для типичного профиля показателя преломления многомодового оптического волокна на длине волны 1300 нм были выполнены расчеты зависимости от радиуса изгиба расхождения оценок постоянной распространения отдельных мод изогнутого световода и прямого прямого световода. Профиль показателя преломления оптического волокна, для которого были выполнены расчеты представлен на рис. 1. Результаты вычислений для отдельных мод представлены на рис. 2. Как следует из представленных результатов, обусловленные изгибом изменения постоянной распространения для мод одного порядка LP ₀₂ , LP ₁₁ практически совпадают. Рассматриваемое расхождение увеличивается с увеличением порядка моды. Вместе с тем, практически во всем диапазоне изменения кривизны волоконного световода, в котором допустимо применение предлагаемого аналитического решения, это расхождение не превышает 1,0 % и можно полагать, что эта величина не зависит от радиуса изгиба.

Таким образом, в работе получено приближенное аналитическое решение в замкнутом виде для произвольной моды изогнутого круглого слабонаправляющего волоконного световода с произвольным профилем показателя преломления. Представлены результаты вычислений для типичного профиля показателя преломления многомодового оптического волокна с диаметрами сердцевины и оболочки 50/125. Показано, что для рассмотренных примеров степень влияния радиуса изгиба на постоянную распространения моды изогнутого волоконного световода возрастает с увеличением порядка моды. При этом, в диапазоне изменений радиуса изгиба световода, в котором выполняются условия применения предложенного приближенного аналитического решения, постоянная распространения мод за счет изгиба световода изменяется незначительно и можно полагать, что это изменение не зависит от значения радиуса изгиба.