Приближенное решение нагруженного гиперболического уравнения с однородными краевыми условиями

Большой класс физических, биологических, экологических и других процессов описывается дифференциальными уравнениями в частных производных со степенной нелинейностью (см., например, [1]). Для их интегрирования, как правило, применяются различные способы линеаризации, часто искажающие суть моделируемого процесса. В методе редукции к нагруженным уравнениям [2] в нелинейном члене исходного уравнения производится замена искомой функции ее следом, что приводит к «ослаблению» нелинейности без ее полного устранения. Найденное затем точное или приближенное решение начально-краевой задачи для нагруженного уравнения можно принять за приближенное решение исходной нелинейной задачи. Подобная процедура применяется, в частности, в [3, 4], где получены формулы общих членов последовательностей приближенных решений начально-краевых задач для некоторых нагруженных уравнений, к которым редуцируются исходные нелинейные уравнения. В настоящей работе предлагается несколько отличный от этого способ нахождения приближенного решения нагруженного уравнения с помощью априорной оценки решения поставленной задачи.

Постановка задачи

В области Q = {(x,t): 0 0,                           (1)

Q где натуральноеp > 3, Q = [0, l].

Уравнение (1) является модификацией нелинейного уравнения, u_tt - a ² u xx + b\u\^p u_t = 0, возникающего в релятивистской квантовой механике [1], а также моделирующего некоторые нестационарные гидродинамические процессы. Нагруженные уравнения вида (1) исследуются в задачах управления, а также могут быть моделями некоторых нелинейных физических процессов. Константы а и b являются параметрами моделируемого процесса.

Требуется найти интегрируемую функцию u ( x , t ) е C ^2,2 ( Q ), удовлетворяющую уравнению (1) в области Q , а также условиям

u ( x ,0) = ф i ( x ), u t ( x ,0) = ф ₂( x ), 0 <  x <  l ,                              (2)

u (0, t ) = 0, u ( l , t ) = 0, 0 <  t <  T ,                                   (3)

в которых ф 1 ( x ), ф ₂ ( x ) е L_p ( Q ).

Априорные оценки

Установим некоторые априорные оценки, которые впоследствии будут использованы для нахождения приближенного решения задачи (1)-(3).

Умножая (1) скалярно на u t и применяя стандартные для подобных случаев несложные преобразования, легко получить неравенства, выполняющиеся для всех значений t е [0, T]:

Бозиев О.Л.                  Приближенное решение нагруженного гиперболического уравнения с однородными краевыми условиями

J ( u t + a ² ^x < q, fc^S C„ |U x |(_n < C 1 ,                  (4)

Ωa где ||v||p n = J v^dx выражает норму функции v(t) в пространстве Lp(Q), а С1 зависит лишь от t.

Ω

Теорема. Пусть решение задачи (1)-(3) u е L p _{- 2}( n ) при любом t е [0, 7 ]. Тогда функция

II u |i p _n ограничена константой, не зависящей от x и t .

Доказательство. Умножим уравнение (1) скалярно на функцию u p "' ( u tt , u p ^{- 1} ) - a ² ( u_xx , u p ^{- 1} ) + b J | u| ^p dx ( u_t , u p ^{- 1} ) = 0.

Ω

Преобразуем по отдельности каждое слагаемое:

( u_tt, u p ¹

1 d t p dt ^г

J u^pdx - ( p - 1) J u t u p ² dx ;

Ω

Ω

- ( u_xx, u^{p - 1} ) = ( p - 1) J u x u^{p - 2} dx ; J | u| ^p dx ( u_t,u^{p - 1} ) = — J | u| ^p dx — J u^pdx .

Ω ΩpΩdtΩ

Возвращаясь к (5) и умножая его на sgn ^pu , приходим к уравнению

1 d ² f p dt ² n

bd

2 p dt

k n

A 2

Ω

u t - a ² u x ) dx ,

после интегрирования которого по t получаем dpb u dx + dt П ' 2

t

k n

= p ⁽ p ^{- 1)} JJ l ^u l p ² ( ^{u t} 0 n

-

a ² u t ) dxdt +

+ dt J | u ( x ,0)| ^p dx + 2

J | u ( x ,0)| ^p dx .

k n          7

Рассмотрим отдельно первое слагаемое в правой части. Применяя неравенство Гёльдера, в котором s = q /( q - 1), получаем при q = 1 в силу первого из (4)

t

J J | ^u|p — ^{2 (}У ^- a ^{2 u} x

0 n

< sup ess x ∈ Ω

1 s

7 t

) dxdt <  J J | u| ^{p 2} dx dt J J| u_t ²

Ω

k ⁰

Ω

-

2 2 au_x

q ।

| dx dt

q

≤

t

JIu|p-2 dx JJ|

Ω

Ω

2 . 2 2 u_t + au_x

dx dt <  sup ess||u|| x ∈ Ω

I p ^-2

I p - 2, n

tC ₁.

К первому сомножителю применим последовательно неравенство Фридрихса [5] и третье из (6), в результате получаем suP ess||u||p-2,n < C2 SUP МЫ1^ x∈Ω                x∈Ω

В итоге оказывается, что t -2                        I С

JJ | u |^p ( u t - a ² ut )dxdt <  tC₁ С ₂ 1 — 1 0 n                              ^k a

f k p ^-2

2 I C1 I21 2 Ik a 7

P — 2

.

C 1 p - C _t a ²⁽ p ^{- 2)} .

Таким образом, от уравнения (6) можно перейти к неравенству dpb udx+ dt n1 2

k n

С 1 ^{p - 1} С 2 a ²⁽ p ^{- 2)}

b t +

I

J Ы p ^dx  ,

k n

после очередного интегрирования приводящего к соотношению

Математика

t ₂

II "I г. bJ (IИ IP,n) dt + K.(7)

в котором при всех t е [0, 7 ] в силу (2)

p-1с_

K > p ⁽ p - 1) ¹ _{2( p} - 2) t ² + - t J|^| ^p dx + Jl^l p dx .

² a ² k n 2 n

Применяя к (7) нелинейный аналог неравенства Гронуолла [6, с. 22], видим, что

II "IIP - C3 = Ч^Т'

Таким образом, теорема доказана.

Приближенное решение

Для нахождения приближенного решения задачи (1)–(3) проинтегрируем (1) по x в границах от 0 до x :

1 ^x p

" x ⁽ x, t ) = ~ J ( " tt ^{+ b}" t |"||p _n ) dx ⁺ A ⁽ t ) a ₀

Применяя к интегралу теорему о среднем значении, запишем последнее равенство в виде l

" x ⁽ x , t ) = /0 2 J ( " tt ⁺ b" t ' " P , _n ) dx ⁺ A ⁽ t ^).

После повторного интегрирования по x получаем выражение x2

"(x, t) = /02 (S( t)+ b5'('t)' ""P,“)+ xA(t)+ B(t), в котором положено

l

J "dx = J "dx = 5 ( t ).

0 n

Удовлетворение условий (3) приводит к соотношению

" ( x , t ) = x ^ ( ^ '( t ) + ^b5'( t )l " II P , n ) .

Применяя к нему (9), переходим к обыкновенному дифференциальному уравнению

^+b|i"iipo ^+^^a2 s=o.

p , П         / 2

Потребуем выполнения равенства в (8) и аппроксимируем (11) линейным уравнением s+be s+^^a2 s=o.

3 l 2

Необходимые для его интегрирования начальные условия получаются из (2):

S (0) = J " ( x ,0) dx = J ф ₁(x ) dx , S (0) = J "_t ( x ,0) dx = J ф ₂(x ) dx .

n         n             n         n

Тогда, при k ₁₂ = ( - /bC 3 ± ^( /bC ₃) ² - 48 a ² ) / 2 / , C 3 >  4д/3 a / lb , находим

S ( t ) =

k ₁

^- k ' 2

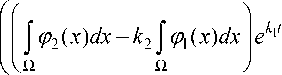
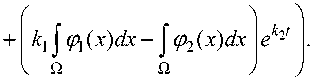
В силу (10) и (11) приходим к формуле приближенного решения исходной задачи:

" ( x , t ) =

2 x

/ ² ( k i - k 2 )

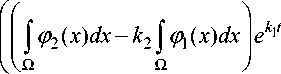
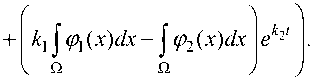
Бозиев О.Л.                  Приближенное решение нагруженного гиперболического уравнения с однородными краевыми условиями

Заключение

В работе предложен способ нахождения приближенного решения задачи (1)–(3), состоящий, во-первых, в переходе от исходного нагруженного уравнения (1) к ассоциированному с ним обыкновенному дифференциальному уравнению (11), а во-вторых, в линеаризации (11) с помощью априорной оценки решения исходной задачи (8). В результате получена формула (12), которая будет, как ожидается, с достаточной точностью аппроксимировать искомое решение, что необходимо подтвердить оценкой его погрешности. Предполагается, что данный способ будет эффективным для нахождения приближенных решений уравнений в частных производных со степенной нелинейностью, аппроксимируемых ассоциированными с ними нагруженными уравнениями.