Приближенное решение обратной граничной задачи для уравнения теплопроводности нелинейным методом проекционной регуляризации

Введение [1]                                               ,                              , h (t) принадлежит пространству C2 [0,^), линейным методом проекционной регуляризации.

.

3 ( 1— £ )

В статье [2] предполагалось, что решение h ( t )e П W 22    (-“,^м) и использован нелиней-

£ >0 .

,                                            [2],

.

Постановка прямой задачи и исследование применимости преобразований Фурье для нахояедения решения

Пусть тепловой процесс описывается уравнением д u(x, t) д2 u(x, t)

—(г22 =   . 2 );0о,(1)

д tдx u (x ,0) = 0; 0 < x < 1,(2)

u(0, t) = h(t); t > 0,(3)

где h (t) - кусочно-гладкая на полупрямой функция, имеющая конечное число точек разрыва первого рода производной h'(t), h (0) = 0(4)

и существует число t ₀ > 0 такое, что для любого t >  t ₀

h (t) = 0;(5)

u(1, t) = 0; t > 0.(6)

u(x, t)                 (1)–(3), (6),     . .,

u ( x , t )e C ([0,1]x[0, -)) П C²¹ ((0,1)x(0,-)).

,                             [3, . 424]

u ( x , t ). Перейдем к исследованию его существования и применимости к его определению преоб- t .

Теорема 1. Пусть Ф( t )e C [0,~) и ограничена на этой полупрямой. Тогда справедливы со

:

w                            -. J u x ( x , t ) ф ( t ) dt =d x

w J u ( x , t )Ф( t ) dt [ 0

и

w juxx (x,t)Ф(t)dt =—2 Ju(x,t)Ф(t)dt

0                        ^d x ² L^J >

Теорема 2. Пусть u (x, t) - решение задачи (1)-(3), (6). Тогда справедливы соотношения ww lim u (x, t)- h (t) dt = lim u (x, t) dt = 0.

x ^0

Постановка обратной граничной задачи

Обратная граничная задача заключается в том, что в постановке прямой задачи (1)-(6) граничное условие (3), определяемое функцией h(t), не известно и подлежит определению, а вместо него в точке x1 е (0,1), измеряется температура f (t) стержня, соответствующая данному процессу u (x1, t ) = f (t); t > 0.                                             (7)

Сведение обратной задачи (1)-(2), (6)-(7) к задаче вычисления значений неограниченного оператора

Пусть Z е L ₂ [0, ~). Элемент h ( t ) е Z тогда и только тогда, когда

где

a

a

- t )=k ¹ t - c -

)² - b ² j

^; c j ^- b j ^ t ^ c j ⁺ b j

^0;                  t <  c j - b j , t >  c j ⁺ b j

a j , b j , c j > ⁰,

с- >  b j и с- * c k при j * k , a y ( t )e W^² [0,~).

Тогда предположим, что при f ( t ) = f ₀ ( t ), участвующем в условии (7), существует функция h ₀( t ), принадлежащая множеству Z , но функция f ₀ ( t ) нам не известна, а вместо нее даны некоторая приближенная функция J₅ ( t )е L ₂ [0, ~) П L [0, ~) ичиело 5 > 0 такие, что

II f5 - f 0|k 5 .                                             (8)

Требуется, используя /§,5,и Z , определить приближенное решение h₅ ( t ) задачи (1)-(2), (6)-(8) и оценить уклонение hh₅ - h ₀|| L приближенного решения h₅ ( t ) от точного h ₀( t ).

Пусть H = L ₂ [0, w) + iL 2 [0, w) - пространство над полем комплексных чисел, a F - оператор, отображающий L ₂ [0, w) П L 1 [0, w) в H и определяемый формулой

F [ h ( t )] =     J h ( t ) e" ^lTtdt ; T > 0.                                   (9)

^п 0

Лемма 1. Опер агор F , определяемый формулой (9), изометричен.

Доказательство см. [1].

Из теорем 1 и 2 следует применимость преобразований Фурье к решению обратной граничной задачи (1)-(2), (6)-(8).

Таким образом, сведем эту задачу к следующей:

д2 z2 (x ,T).

—— = ITU (x ,T); x e( 0,1), T > 0,(10)

_______________ дx 2013,     5,1

Математика

где u(x,т) = F[u(x,t)]. (6)–(7), й (1,т) = 0; т > 0(11)

й (Х1,т ) = / (т); т > 0,(12)

где f ( ^т ) = F [ f ( t )].

Из теоремы 2 следует, что решение й(x,т) задачи (10)-(12) непрерывно в полосе [0,1]х[0, ^). При этом решение уравнения (10) имеет вид й (x, t) = A (т)e'x^ + B (т) e--x^,

где ^0 = -^(1 + i), a A (т) и B (т) - произвольные функции. (11)–(13)         , h (т) = —        .f (т), т > 0.

sh д ₀(1 - x 1 ) 4т

Предположим, что х 1 < Л, а т е [0,2].

Так как

(15)          ,

sh ц0 4т	ch 42т - cos 42т
sh ^ 0 (1 - x 1 ) 4т	ch (1 - x 1 ) 42т - cos (1 - x 1 ) 42т

,

sh Ц0Ч т sh д0(1 - x 1) 4т ch X - cos X ch (1 - x1) X - cos (1 - x1) X ’

где X = 22т .

,    (16)           ,

Теперь оценим функцию

Так как

sh ц₀ ^т

sh ц0 4т <^ 2 (e2 +1) sh ^0 (1 - x1) 4т e - 2 при т > 2.

sh ^ ₀ у т sh ц₀ (1 - x 1 ) 4т

ch л

^- cos^{(1 -} x 1 ) 42г sh (1 - x 1

<

2 e ²

- e

,

x ₁

sh д ₀(1 - x 1 ) V ?

т > 2.

Так как

2 ( e ² +1) >4,

V e - 2

где

sh д ₀ V r

sh д ₀(1 - х ₁) V t

a =

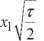
t > 0,

2 ( e ² +1) V e - 2 ^.

Решение задачи вычисления значений неограниченного оператора (14) нелинейным методом проекционной регуляризации

,                                       (1)–(2), (6)–(7)             -

T ,

L 2 [0,^м) в L ₂ [0, ~) и определяемого формулой

Tf ^ =   sh Д0 ^т   f ^), т > о, sh(1 - хДд 4т

где Д о =    (1 + i ), f , Tf е H .

(14)                                                 :

h ( т ) = Tf ( т ); т > 0.                                    (22)

Обозначим через Z множество функций из L ₂ [0, ^), определяемое соотношением

Z = F [ Z ],

F                         (9),                     (22)                                   -

T .

ˆˆ

ˆˆ

Предположим, что при f (т ) = f 0 (т ) существует элемент h ₀ ( т )е Z , но точное значение

f ₀( т ) нам не известно, а вместо него даны fg ( т )е H и 5 > 0 такие, что

II 5 Т )- f (ф 5 .                           (24)

Требуется, используя исходную информацию fg ( т ) и 5 , определить приближенное значение h₅ ( т ) и, учитывая принадлежность h₀ ( т ) множеству /^/. оценить величину уклонения I ^h5 ( ^т )^- h 0 ( ^т )||.

Для решения поставленной задачи введем регуляризующее семейство операторов { T_a : a > 0}, определяемое следующим образом:

Taf Т )

Г л ,

Tf ( т ); т <  a

,

0; т >  a

a > 0,

T                        (21).

Таким образом, приближенное значение hig (т) неограниченного оператора T определим формулой hia = Taf5 (Т) ,                                        (26)

в которой оператор T_a определен (25). Параметр a = a

( fg , 5 ) в формуле (26)

определим из

уравнения

II T "^j his ( т )- f ( т )||² = 9 5 ².                                   (27)

,                                                         1           [4],                                ,

II T ¹ hig ( т )- fs ( т ) е C [0, ~) не убы Baerno a , а также стремится к || 5 npn a ^^HKHynro

Математика

при а^ 0 . Из того, что / >  93¹ следует разрешимость уравнения (27). Заметим, что в случае неединственности, решения уравнения (27) совпадают с отрезком [а₁,а₂ ] и для любого а е [ а ₁, а ₂ h§ = ha ¹ . Потому среди всех решений выберем минимальное. Из непрерывности T                                                                     (27).

Таким образом, приближенные значения hig (т) задачи (22), (24) определим формулой ha (т) = pr ^^^М; H0

где H о = F [ L 2 [0,-)].

Оценка погрешности || hia ( т )- h ₀ ( т )|| приближенного решения hia задачи (22), (24)

Перейдем к оценке уклонения || hia ( т ) — h₀ ( т )|| приближенного ˆ     ˆˆ

значения ha (т) от точного h0 (т). Так как h0 (т)е Z , то на основании (23) существует число c > 0 такое, что для любого т > 0 справедливо соотношение

I h ^{0 ( т} Ч⁵

Из (29) следует существование числа d >  0 такого, что для любого £ е

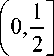
W

j[^{1 + т3(1-6} ) ]| ^h 0 ( ^т ) ^{dт 5} £ •

Iotv* TZOTz*

h 0 ( т )е H 0,

,                  [2],                     (28), (31)          ,

I ha (т)- ^0 (т)||5 6 ^Ge [a(a,£)], где функция Ge (а), следуя (14), (19), (20) и (30) определена параметрически: а = ae ’^2, Ge (т) = [1 + т3(1-£)] 2; т> 0, a a(a,£) определена уравнением drc^H^ a.

N £ а

Так как оценка (32) выполняется при любом £ е f 0,1

, то выберем значение £ ( a ), миними-

,

⁶J ? ij G i a ) И⁵'^{£ ( a )})J = _{£ e}m₀ⁱnj⁶ ^G£ ^'^;'^,£

Из (32)-(35) для hia ( т ) будет справедлива оценка

I ha ( ^т )^- h 0 ( ^т )||

(36),                                                        .                            , ге Г0,2

G _e ( с ) =

1 +

Г ₂ уо- г )

I Х 2 J

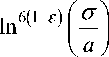
Из (37) следует, что при с >  а и г е

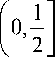
G, ( с )<

2 12 (‘-г)            / x1          ln-3(1-г) I с

2               I а

Из (37) и (38) следует, что при с >  а и ге

lim с^~ г 2 Х‘

G_E ( ^с )

= 1,

ln^{-3(1- г} ) I ^С ( а

а из (37) и (39) следует существование с >  а так ого, что для любого с >  с и г е

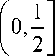
G_e ( с )>

13(‘—г)            Г x‘         ln-3(‘-г) I С

2               ( а

, lim с^~

с

13(‘-г)            е x‘         ln-3(‘-г) | С

2                ( а

= 0

следует существование числа с₂ >  с такого, что

при с >  с₂

Г 13(‘-г)/ л с    x‘         ln-3(‘-г) |^),

2I а из последнего соотношения и (40), что для любого с > с2

Цг < -Ge (с).(41)

с ² с

Пусть а ( ^ , г ) определено уравнением (34), а а ( 5,г )

daa ^2 = 5.(42)

(42),

О" (5г ) = 4К-(43)

г5 ²

(34), (41) (42),

а(5,г)< а(5,г).(44)

Таким образом, из (32), (38) и (44) следует существование числа 50 > 0 такого, что для любо го 5е (0,50) и ге

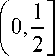
Математика

„         , Г     ^{3(1 - Е} )             ( s

Нг < х ; , J|² -,d x          -3(1- ^ ос(8,£)

hs М^- h o ( ^Т ) < 36- v ^{in (} )       -

^{11                   11} el                      ^ a J

Из (44) и (45) следует, что при J e ( 0, s ₀) и e g

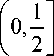
||hs ( Т )- h o ( г )|f <36 ^' in ^{- 3(1 - E} ' fIE!]

^{11                  11} e                    I a \s8^z J

Пусть

E ( ^S ) =

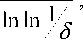
(46)          ,

hs ( ^T )^{- h} 0 ( ^Т )|

< 36 - in in in ³

s

- v 4 a E(s)s2

in ^{E ( s} )

4 —;------- 7

^ a E ( S ) s⁴

Предположим, что число S 1 >  S_o определено соотношением

S' -A , 1 1 -1-4-in in— < 1 .

a

S i

Тогда при S g (0, S 1 ) из (47)

h₈ ( t) - h₀ ( t   < 36 - inin—in ³

^o                S

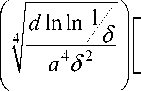
in ^E < ^s l s

Так как при s g (0, s 1 )

e ( s ) < 1 A 1            1

inin I I =------inin- = 1,

I s J 1 1 1 s lnln

s

(49)          ,

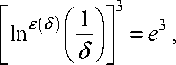
(48) (50),

h_s ( t) - h₀ Т < 36 -e ³inin—in^{3 0}                   s

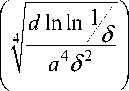
1 a ⁴

Предположим, что s ₂<  s ^и in in — > —, тогда при s g (0, s₂) ^{1               21} s ₂ -       ^{1 x}

1 d lnln

s

42 a d

> ~T.

Таким образом, из (51) и (52) следует, что при s g (0, s ₂)

hs ( ^Т )^{- h} 0 ( ^Т )|

< 36 - e ³ in in— in ³1 —1 . s I s J

Из (53) следует, что при s g (0, s ₂) справедливо соотношение

I his ( ^Т )^{- h} 0

(

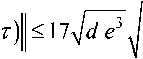
1    - ³

lnln ln ² s

Камалтдинова Т.С.           Приближенное решение обратной граничной задачи для уравнения теплопроводности нелинейным методом проекционной регуляризации Литература

• 1.                 , . .-

  / . .                   , . .//

  . – 2010. – . 16,   2. – . 238–252.

• 2., . .

• -                                               / . .                   ,       . .                            , . .//

  . – 2012. – . 18,    1. – . 281–288.

• 3.            , . .                                           / . .            . – .:         , 1968. – 576 .

• 4.                , . .                                                                                                                 -/

  • .    .          , . .             //                                                                    . – 2006. – . 9,4.

    – . 353–368.

APPROXIMATE SOLUTION OF INVERSE BOUNDARY PROBLEM

FOR THE HEAT CONDUCTIVITY EQUATION BY NONLINEAR METHOD OF PROJECTION REGULARITY

T.S. Kamaltdinova ¹