Приближенное решение в области аналитичности одного нелинейного дифференциального уравнения

УДК 517.928.4

ПРИБЛИЖЕННОЕ РЕШЕНИЕ В ОБЛАСТИ АНАЛИТИЧНОСТИ ОДНОГО НЕЛИНЕЙНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ

В. Н. Орлов, М. П. Гузь

В работе построено приближенное решение в области аналитичности для одного нелинейного дифференциального уравнения, с подвижными особыми точками, в общем случае не разрешимого в квадратурах. Улучшены оценки, полученные авторами ранее.

В работе [1] была рассмотрена задача Коши для нелинейного дифференциального уравнения в нормальной форме.

У'(х) = У⁴(х) + г ^ х ),           (1)

У(х0) = У0.               (2)

Для коэффициентов разложения решения данной задачи в области аналитичности го

У = Е С„ (х - д0)” о была получена оценка

|С„ < - ■ М ₂ ■ 2² ” ^-1 ■ ( М ₂ + I ) ³ ” , где

[.                      ( ^х ° )|

М2 = шах t уо , sup ---------1 >, и = 0, 1, 2, ... ,

которая в данной работе улучшена.

Теорема 1. Пусть:

1) г(х) е С ” в области К = ^ х : х -- Д о < Р1, Р1 > 0 } ,

2) 3 M _t

/"* ( х ) и !

< М ₁,

х е К

где М \ = const, и = 0, 1, ... .

Тогда решение задачи (2) — (3) является аналитической функцией

”

^У ( ^х ) = Е ^Си ( ^{х - х} 0 ) ”         ⁽³⁾

в области К2 = {х : |х - х0 < р2, р2 > 0}, где

Р 2 = min ^р_ь

2² ( М 2 + 1 ) ³

М 2 = max ^ У о ,

М₂ = max А |У о , sup

|г < ^{и )} ( х о )| и!

и = о, 1, 2, ...

sup п

1 r^W ( ^х 0 ( п!

п = 0, 1, 2, ...

Доказательство.

По условию теоремы имеем:

№

г(х) = 2 А „ (х - х₀) ^и .

о

Подставим данное выражение и ряд (3) в (1):

Предполагая оценку для Сп:

I С_и\ <  ¹ • М₂ • 2^{2 и- 1} ( М₂ + 1 ) ^{З и} ,      (8)

и методом математической индукции докажем ее справедливость.

Из (8) имеем:

( п + 1) С п ₊ 1 = В „ + А п .

Из последнего с учетом оценки (8) и условия (1) теоремы 1 следует:

।^{Сп+ 1}<  _{п + 1} (I ^{D + А} I) <  _{п + 1} (I ^dA ^{+ Ап} ) <

2 С_пп ( х - х о ) ^{и- 1} =

№                  А

2 ^С„ ( ^{х - х} о ) ” I + . о                       )

№

+ £ А „ ( ^х - ^х о ) ^и . о

<---- п + 1

f

У Ц Ц П — 1 1

( 1 =0

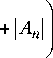
Выполнив соответствующие операции, получим:

от 2 с„ п п 1	п - 1 ( х - х 0 ) + 2 А ^ ( х 0	= 2 2 D п ( х - Х 0 ) п + 0                 (5) - х 0 ) п >
где
^ и =	и = 2 С и - i C i , 1 = 0	и = 0, 1, 2, ... ,
D * = и	и 2 О и - i D i , 1 = 0	и = 0, 1, 2, ... .

х

или

1 С” +11< и + 1 \	и 7 п — 1            А	7 1           А
	2 | 2 С и — 1 — усу I 1 = 0 (/ = 0            )	1 2 Сг — k C j 1 1 1 = 0          J	+

1 < ---- и + 1

п п - г

2 2

( г = о ( / = 0

• М₂ х

⁺ Ии

(п - г - д

X 2^{2( п-г-i ) - 1} • (М₂ + 1)^{3( п-г-} О -1 • М₂ • 2^{2 i-1} х

₃ ; А (

^(М 2 ⁺ О ² I • 2

(г - УУ

■ М 2

■ ₂2(1 - /М

Равенство (5) обратится в тождество при условии:

и • С_и = D *_{- 1} + А_{и - 1}, и = 1, 2, ... . (6)

X (М₂ + 1)^{3( г-у )} ■ 2 . М₂ ■ 2² i ^{- 1} ■ (М₂ +1)³ i I I + 71                           JJ

+ М 2 l<

п + 1

Соотношение (6) позволяет однозначно определить все коэффициенты Сп.

Таким образом, получили формальное единственное представление решения задачи (1) — (2) в некоторой окрестности точки ^х о в виде (3).

На втором этапе докажем сходимость ряда (3). Обозначим:

М 2 ⁴ I

■ 2^{2 п- 4} ■ (М₂ + 1)^{3 п} x

X

п п — 1

2 2

( 1 =0 ( j =0

(п — 1 — Д

--X

7 +1

: 2 —--;— j=o ^1 — 7^1

к

J ¹J

I +1 <

J

<       ■ М2 ■ 22п+1 ■ (М2 + 1)3п+3, п + 1

при этом

X |д

IN+ 1 ^д 0

■ ------------т;------------------------~.

1 - 22(М2 + 1)3 д - д0

1, если j = и - г; г = 1;

( и - г - j ) ₁

= ^ и - г - j, если j = 0, ...,

V д е ^ 2 = { д : д - Д о < Р 2 , Р 2 > 0 } ,

„ „ L 1

где р2 = min р , -5----------

²          [    2² ■ (М₂ + 1)

и - г - 1; г — 0, ..., и - 1;

fl, если j = 0;

[ j, если j = 0, ..., г;

'           |/^п)( д о )|

М 2 = max < |У о , sup ----------

и = о, 1, 2, ...

1, если j = и - г; г = 1;

( г - j ) ₁ = 5 ( г - j ) , если j = 0, ...,

Доказательство. С учетом оценок для коэффициентов С_и, полученных в теореме 1, имеем:

и - г - 1; г = 0, ..., г - 1.

Рассмотрим ряд ^го

Е1 • М2 • 22 1• (М2 + 1)3п • д - до и, о п являющийся мажорантой для ряда (3).

На основании признака Даламбера получаем сходимость этого ряда в области

<       1

22(М2 + 1)3 '

Окончательно получаем сходимость ряда (3) в области

|^{д - д} 0 <  ^р 2 -

Таким образом, завершено доказательство теоремы 1.

Оценки, полученные в теореме 1 для коэффициентов С_и ряда (3), позволяют построить приближенное решение задачи Коши (1) — (2)

I У - У ^ <

<

N yn = Е сп (д - до)п. о

Теорема 2. Пусть выполняются пункты 1 и 2 теоремы 1, тогда для приближенного решения (9) задачи Коши (1) — (2) справедлива оценка погрешности

IУ - У < -^— • М₂ • 2 ^{2n + 1} • (М₂ + 1)^{3 У+ 3} X

¹       ”' N +1     ^{2               2}

го                   N

Е ^Сп ( ^{д - д} 0 ) ” ^- Е ^Сп ( ^{д - д} 0 ) ”

0                     0

го

Е ^Сп ( ^{д - д} 0 ) ^п

N + 1

го

< Е ¹ ■ М₂ ■ 2^{2 п- 1} x

N + 1 ^п

<

x (М₂ + 1)^{3 п} ■ |д - д₀ |^п< —— ■ М₂ ■ 2 ^{2n + 1} x

^{2          1      01} N +1     ²

x (М₂ + 1) ^{3 N+ 3} • |д - д ₀|^{N+ 1} x

1 X                                             .

1 - 2 ² • ( М₂ + 1) ³ • |д - д₀|

Пример 1. Рассмотрим задачу Коши для уравнения У' ( д ) = У⁴ ( д ) + г ( д ), где

г ( д ) = о, У (1) = 1.

Задача Коши имеет точное решение

3/3Д^4 ■

Вычислим радиус аналитичности с учетом начального условия задачи Коши.

р2 = -----------5- = 0,0560039177.

² 2² ■ (М₂ + 1)³

Выберем значение д = 0,12в полученной области аналитичности.

Все расчеты представлены в табл. 1.

Таблица 1

^ 0	X	У	У 3	А	А 1	А 2
0,1	0,12	0,6500791007	0,6500791026	0,0000000019	0,0109049371	0,0000014

Здесь Y — точное значение решения уравнения; Y 3 — приближенное решение; Д — абсолютная погрешность; A_t — априорная погрешность, полученная по теореме 2; Д₂ — апостериорная погрешность.

Теорема 2 позволяет решить обратную задачу теории погрешности, определить значение N по заданной точности приближенного решения s. Для случая s = 0,0000014 получаем значение N = 13. Фактически для N =4, 5, 6, 7, 8, 9, 10, 11, 12, 13 получаем уточнения приближенного решения, которые в общей сумме не превышают требуемой точности s = 0,0000014.

Таким образом, мы можем ограничиться в структуре приближенного решения значением N = 3. При этом получаем величину Д 2 апостериорной погрешности для приближенного решения Y 3 , равную значению s = = 0,0000014.

При получении приближенного решения дифференциального уравнения часто приходится осуществлять аналитическое продолжение. Эта операция приводит к задаче: исследование влияния возмущения начальных условий задачи Коши на аналитическое приближенное решение рассматриваемого нелинейного дифференциального уравнения. При этом получает возмущенное начальное условие

У Сг₀) = У_о.              (10)

Возмущенное начальное условие (10) оказывает влияние на структуру аналитического приближенного решения (3), которое принимает следующий вид:

w -V                             -V

Y_nU) = £ С„(х - х₀) ^и ,      (11)

о где Сп — возмущенные значения коэффициентов.

Теорема 3. Пусть:

1) г(х) е С ” в области К = ^ х : х -- ^х 0 < Р 1 , p t > ⁰ } ;

ДУ/ v ( ^х ) — Д 1 + Д 2 в области

Iх - Х 0 < Р 4 , где

Д! —       • М₂ • 2^{2n + 1} • (М₂ + 1)^{3 y+ 3} X

¹ N +1    ^{2            2}

X Iх

I N + 1 ^х0

Д2 < ДМ

М 2

= max <

r^W ( ^ 0 ) п!

где М ^ =

• = const, и = 0, 1, ... ;

• 3)    известна оценка погрешности Y 0 -

  - Y0| = AY 0 .

Тогда для аналитического приближенного решения (11) задачи Коши ((1), (10)) справедлива оценка погрешности

_________________1_________________

1 - 22 • (М2 + 1)3 |х - х0,

2 ■ (М₂ + ДМ + 1) ³ |^х - х ₀|

1 - 22 ■ (М2 + ДМ + 1)3 |х - х0

ДМ = ДУ0,

IY0

I ^'>( Х 0 )| , sup-------------

Р 4 = min { р 2 , р₃ } ,

и = 0, 1, 2, ...

^{Р 2} = “'” ^{| Р 1 ,} ₂ 2 .(М ₂ + 1) = ' •

РЗ = —з------------------у .

2² ■ (М ₂ + ДМ + 1) =

Доказательство. Используя классический подход, получаем:

ДY_N(х) = Y(х) - Yy(х)| < |Y(x) - Y_n (х +

+ |Yjv (х) - Y_y (х)| <

<

£ С_и (х - х₀ ) ^и 0

N

- £ С_и (х - х₀ ) ^и 0

+

+

N

£ С_и(х - х₀) ^и 0

- £ б_п(х - х 0 ) ^и

£ С „ (х - х 0 ) ^и

N + 1

+

<

+

N

£ (С п

- С „ )(х - х 0 ) ^и

— £ ^_и(х - х₀)^и| + I ДС „ |х w + l                о

<

^{- х} 0Г ^{— Д} 1 ^{+ Д} 2 ,

где

|С - с_п\ = а С „ .

Выражение для А 1 следует из теоремы 2.

A_t<       • М₂ • 2^{2n + 1} • (М₂ + 1)^{3 N+ 3} х

• 1    N +1    22

I          IN+1

х х - х.

• 1    - 2² • (М₂ + 1)³ |х - х₀|

На основании рекуррентного соотношения для коэффициентов структуры приближенного решения (3), (6) имеем выражение:

С = Р3й+1 (Со, А), Д, А2, ..., А3п), где правая часть соотношения представляет собой полином степени 3и + 1 с положительными значениями элементов. При этом Со = = У о — начальное условие (2), Ло, X, А2, ..., А3п —коэффициентыразложенияфун-кции г(д) уравнения (1) в ряд. Тогда для выражения аС„, учитывая закономерность образования коэффициентов Сп и их оценку (8), методом математической индукции получаем оценку асn+1 <      • 22N+1АМ(М2 + АМ + 1)зу+3,

N + 1

где АМ = А С ) = А У ) — возмущение начального условия задачи Коши.

Таким образом, для А2 получаем оценку го                                        го

< 2 АС „ ■ |^д - д о |” = ^{А С} о ⁺ 2 АС „ ■ |^{д -} д |” <  о                                      1

< АМ ■

] +   2(М2 + АМ + 1)3 |д - до v 1 - 22 ■ (М2 + АМ + 1)3 д - до

■

Оценка А 2 справедлива для области

I Д - До < Рз = ---------1----------т .

• ^{1     01}        2² . ( М ₂ + А М + I)³

Окончательно выражение АУ у ( д ) будет справедливо в области

Iд - Д о < р₄, где

Р 4 = min { р 2 , р з } ,

Р 2 = min

Р 1 >

22 • (М2 + 1)3

Пример 2. Строим аналитическое продолжение для приближенного решения задачи Коши в примере 1.

Начальное условие задачи Коши Д о = = о,12, У ) = о,65оо77ооо. Величина возмущения не превышает значения е = 0,0000014.

Все расчеты представлены в табл. 2.

ГО

2 ( с „ - С „ ) . ( д - Д _О ) ” о

Таблица 2

Д о	Д	У	Y 3	А	а ;	а 2
о,12	о,143	о,6542394327	о,6542373178	о,ооооо21	о,о2156355	о,ооооо39

А ₂ =

Здесь У — точное значение решения орная погрешность, полученная по теоре-уравнения; У 3 — приближенное решение; ме 3; А ₂ — апостериорная погреш-А — абсолютная погрешность; А * — апри- ность.