Приближенные двумерные уравнения для вихревого течения в плоском слое с твердыми границами

В работах [1–3] описывается подход и приводятся приближенные уравнения для расчета турбулентных течений в плоском слое жидкости с твердыми границами (Рис. 1) в безразмерном виде:

5 V x + <2 + 5 VV

5 1     5 x      5 y

5 V y , 5 V x V y + 5^

5 1      5 x      5 y

• -^ + A V, + KV + K VVx + Sfx,-|p + A V, + KV +K2 VIV, + Sf,,

  
  

5V

—- +-- = 0

5x

Здесь приняты обозначения: A = 52/5x2 +52/5y2— оператор Лапласа; |V| — модуль средней скорости по высоте слоя; Vx, Vy — средние по высоте слоя планарные

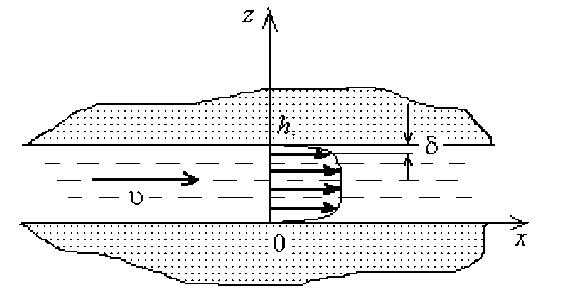
Рис. 1. Тонкий слой жидкости между параллельными твердыми стенками; δ ∼ 1 / υ – ламинарный подслой

компоненты скорости жидкости ( υ — скорость жидкости в какой-либо точке потока); p — давление (в приближении тонкого слоя оно считается постоянным по высоте слоя);

κ 1 и    κ 2

—

эмпирические коэффициенты, определяемые из специальных экспериментов [4]. Также введен безразмерный комплекс   S = ( f0h3 )/(pv2), где ρ — плотность жидкости, h — толщина слоя, ν — кинематическая вязкость жидкости, f0 — характерное значение объемных сил в слое. Параметры h , ν h и f0 являются, соответственно, единицами длины, скорости и объемных сил.

Основная идея при получении этих уравнений состоит в том, что вместе с приближением тонкого слоя планарные компоненты скорости задаются в виде:

υ _i = V_i ( x , y ) ϕ ( z ),

после чего это выражение подставляется в уравнения Навье–Стокса и уравнение непрерывности. Далее (с использованием приближения тонкого слоя) уравнения усредняются по поперечной координате. При этом полагается, что в турбулентном течении жидкости основное трение сосредоточено в вязких подслоях вблизи верхней и нижней стенок слоя. Трение же за счет сдвиговых течений в плоскости слоя менее существенно и играет вторичную роль.

В таком подходе функция ϕ ( z ) описывает профиль осредненной скорости течения жидкости в слое. Вполне достаточно, чтобы этот профиль был выпуклым и, в случае турбулентного течения, более уплощенным, чем квадратичный, но на верхней и нижней стенках нормальные к ним градиенты скорости течения должны наилучшим образом соответствовать реальному процессу. Задание конкретного вида функции ϕ ( z ) при этом не является обязательным: достаточно знать лишь значения нормальной производной от этой функции на нижней и верхней стенках слоя.

Действительно, член уравнения движения, отвечающий за трение жидкости с учетом приближения тонкого слоя и осреднения уравнения поперек слоя принимает вид:

• V ( x , y ) ^∂ϕ ( z )¹.

∂ z ₀

При ламинарном течении производная ∂ϕ(z) ∂z будет постоянной и равной 12 [5]. В случае турбулентного течения вопрос о ее величине более сложен, так как не представляется возможным точное определение формы профиля течения. Однако при турбулентном течении вблизи стенок канала имеется тонкий ламинарный подслой, и производная скорости на стенке может быть приближенно определена как отношение скорости потока на границе слоя к толщине этого подслоя. При развитом турбулентном движении профиль осредненной скорости потока уплощен, поэтому приближенно можно считать скорость одинаковой по всей толщине слоя. Кроме того, толщина подслоя обратно пропорциональна числу Рейнольдса Re. Для выбранного случая единиц размерности выполняется условие: Re = V=v/(v/h). По этой причине на нижней (z = 0) и верхней (z = 1) твердых плоскостях, ограничивающих слой, для производной от профильной функции ф(z) по z ставится условие:

бф/ z ) /5 z = ± 0,5 ( к 1 + k₂ V I).                                                         (3)

Здесь _К 1 и _к 2 — эмпирические константы, отвечающие, соответственно, за ламинарное и турбулентное трение.

Подобная процедура получения уравнений движения выглядит естественно для описания проточных течений через плоские каналы. Однако если в плоском канале рассматривать планарное вихревое течение (Рис. 2, а ), то его поперечный профиль будет уже существенно другим. Действительно, так называемые центробежные силы в ядре планарного вихря приводят к появлению вторичного индуцированного течения. Это течение расходится в средней части слоя из центра вихря и сходится к его центру вблизи верхней и нижней стенок канала в областях, где жидкость заторможена (Рис. 2, б ). Таким образом, истинный профиль течения не является выпуклым, и представление скорости в виде выражения (2) может быть неприемлемым.

Для того чтобы учесть возвратные течения при вихревом движении жидкости в плоском слое между твердыми стенками, представим планарные скорости жидкости

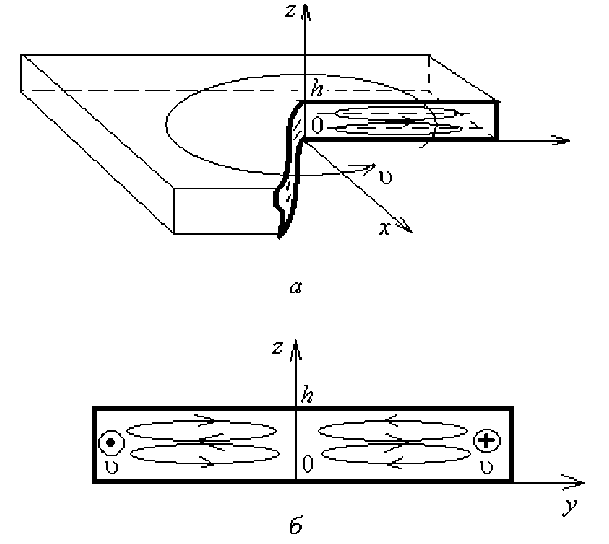
Рис. 2. Течение жидкости в тонком слое, ограниченном твердыми стенками: вихревое ( а ); возвратное, индуцированное планарным вихревым движением ( б )

в виде ряда по базисным функциям ф :

V = V i ⁽ x , У ) Ф 1 ( z ) + ^r i ⁽ x , y ) Ф 2 ⁽ z ).

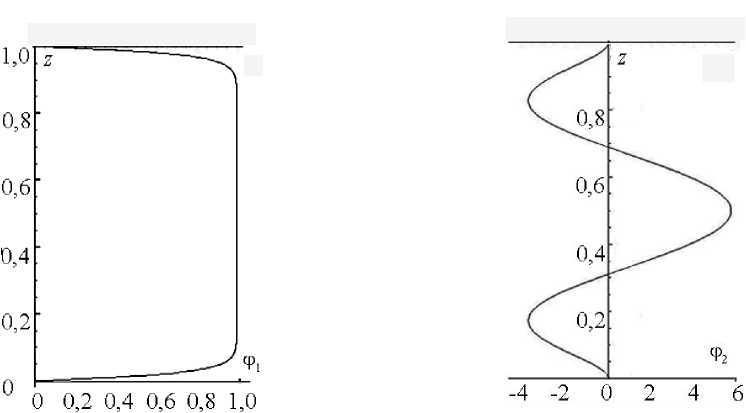
Здесь первая функция ф 1 ( z ) отвечает за выпуклый профиль течения жидкости (Рис. 3, а ), а вторая, ф ₂( z ), — за возвратные течения, возникающие в сечении слоя (Рис. 3, б). Эти функции должны удовлетворять вполне очевидным условиям, которыми являются условия нормирования и условие максимума функции в центре слоя. Условия, в свою очередь, накладывают на вторую базисную функцию требования, согласно которым ее подстановка в выражение для скорости не должна «портить» значения производной от скорости на стенке и должна позволять скорости на стенке обращаться в нуль:

J ф 1 ( z ) dz = 1, J ф 2 ( z ) dz = 0,

J ф ₂( z ) dz = 1, дф ₂( z )/5 z = 0

( при z = 0,5 ) ,

ф ₂( z ) = 0,    дф ₂( z )/5 z = 0 ( при z = 0 или 1 ) .

Удовлетворяющими этим условиям и условию (3) функциями являются следующие:

1 + 2 m        2 m    2 m ф1 =         1(1 - z) + z - 11,

1 - 2 m ф2 = -545,03335z2 + 3634,24231 z3 -8177,56016z4 + 7632,52681 z5 -2544,17560z6, m = 0,25(к1 + к2 V|) .

Так как в рассматриваемой ситуации V = Re , то 4 m « Re . Таким образом, после представления скорости в виде (4) появляется пять переменных ( V x , V y , Г х , Г у и р ), которые необходимо найти для описания течения в слое. Для их определения подставим выражение (4) в уравнения движения (1), после чего произведем две операции:

а

б

Рис. 3. Вид профильных функций ф ₁( z ) и ф ₂( z ) (функция ф 1 приведена для значения параметра m = 50)

во-первых, проинтегрируем уравнения по z от 0 до 1; во-вторых, умножим уравнения на функцию ψ и проинтегрируем их по z от 0 до 1 (функция ψ должна удовлетворять 1

условию ∫ ϕ ₁ ψ dz = 0). В рассматриваемом случае функция ψ равна: ψ = 1 - 2 z .

Таким образом, для искомых переменных получается система приближенных уравнений, которая для достаточно больших m (практически всем реализуемым течениям соответствует m >  100) представима в виде:

∂ V   ∂ V ²

^x + ^x ∂ t ∂ x

² ∂ VV

-0,00196 Vxх +0,0744 x +y х -∂x∂

∂ Г V ∂ VГ ∂ ГГ

-0,00098 yx-0,00098 yх +0,0744 yx=-∂p+ΔV-4mV+Sf, xxx

∂ y ∂ y ∂ y ∂ x

∂V ∂VV        ∂VГ         ∂ГV        ∂ГГ∂

^y + ^{х y} - 0,00098 ^xy - 0,00098 ^{х y} + 0,0744 ^xy + ^y -

∂t∂x             ∂x             ∂x∂

∂V Г∂

• - 0,00196 ^yy + 0,0744 ^y =-^{∂ p} +Δ V - 4 mV + Sf , ∂ y     ∂ y ∂ y^yyy

∂V∂ х+ y=0 ∂x∂y

• ²         ∂ Г V ∂ VГ

  • - 0,1081 ^x - 0,2162 ^Vxx + 0,0003 ^x - 0,1081 ^yx - 0,1081 ^yx +

∂ t ∂ x ∂ x ∂ y ∂ y

∂ ГГ

+0,0003  yx=-0,1081ΔГ-0,001Г, xx

∂ y

∂ Г       ∂ V Г ∂ ГV       ∂ ГГ       ∂ V Г

• - 0,1081 ^y - 0,1081 ^xy - 0,1081 ^xy + 0,0003 ^xy - 0,2162 ^yy +

∂ t ∂ x ∂ x ∂ x            ∂ y

+ 0,0003    ^y = - 0,1081 Δ Г - 0, 001 Г ,

∂y                y y где fx , fy — проекции электромагнитных сил на соответствующие оси координат.

Как видно, в группе уравнений (5) есть члены, величина которых мала в сравнении с другими (об этом свидетельствуют коэффициенты при них), и если этими малыми членами пренебречь, то группа уравнений (5) станет тождественной системе уравнений (1). Группа уравнений (6) не содержит в явном виде планарных компонент объемных сил, и это говорит о том, что возвратные течения, описываемые Г х , Г у , генерируются через течения с выпуклым профилем V x , V y . Следовательно, возвратные течения, которым отвечает второй член разложения (4), в границах приближения тонкого слоя и ограничения на область рассмотрения течений, определяемых числом Рейнольдса, значения которого начинаются с нескольких сотен, оказывают слабое влияние на основное течение.

Таким образом, гидродинамические процессы в плоских каналах, описываемые через локально осредненные по толщине канала планарные компоненты скорости, могут достаточно хорошо рассчитываться с использованием только системы уравнений (1). Это положение подтверждается удовлетворительным совпадением экспериментальных и расчетных результатов [1–3], при получении которых использовалась система уравнений (1). Однако такое положение справедливо для случая, когда движение жидкости не оказывает заметного влияния на объемные силы, генерирующие это движение. В случае, когда такое влияние существует (например, проводящая жидкость находится в магнитном поле и ее движение обусловлено электромагнитными силами, а влиянием движения жидкости на магнитное поле пренебречь нельзя), уравнения (5), (6) будут иметь другой вид и возвратные течения могут играть существенную роль.