Приближенные решения многомерных сингулярных интегральных уравнений и быстрые алгоритмы их нахождения
Автор: Васильев Александр Владимирович, Васильев Владимир Борисович
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 1 т.16, 2014 года.
Бесплатный доступ
В работе получена оценка разности между континуальным и дискретным сингулярными интегралами в многомерном пространстве. Предлагается использование быстрого преобразования Фурье для нахождения приближенного решения уравнений, содержащих такие операторы.
Ядро кальдерона - зигмунда, дискретный сингулярный интегральный оператор, приближенное решение, быстрое преобразование фурье
Короткий адрес: https://sciup.org/14318450
IDR: 14318450
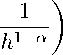
Список литературы Приближенные решения многомерных сингулярных интегральных уравнений и быстрые алгоритмы их нахождения
- Абдуллаев С. К. Многомерный сингулярный интеграл в пространстве Гельдера с весом//Современные проблемы теории функций. Материалы всесоюзной школы по теории функций.-Баку: АГУ, 1980.-С. 43-48.
- Абдуллаев С. К., Васильев В. Б. Об одной кубатурной формуле для многомерного сингулярного интеграла по ограниченной $m$-мерной области//Докл. АН Азерб. ССР.-1983.-\No 11.-С. 16-19.
- Абдуллаев С. К., Васильев В. Б. К приближенному решению многомерных сингулярных интегральных уравнений//Приближенные методы решения дифференциальных и интегральных уравнений.-Баку: АГУ, 1983.-С. 17-26.
- Васильев А. В., Васильев В. Б. О дискретных свертках//Тр. междунар. школы-семин. "Методы дискретных особенностей в задачах математической физики".-Орел, 2009.-Вып. 7.-С. 31-35.
- Васильев А. В., Васильев В. Б. Дискретные операторы Кальдерона~-Зигмунда: некоторые наблюдения//Тр. XIV междунар. симпозиума "Методы дискретных особенностей в задачах математической физики". Ч. 2.-Харьков-Херсон, 2009.-С. 257-260.
- Васильев А. В., Васильев В. Б. Дискретные варианты некоторых интегральных операторов и уравнений//Тр. междунар. школы-семин. "Методы дискретных особенностей в задачах математической физики".-Орел, 2010.-Вып. 8.-C. 29-33.
- Васильев А. В., Васильев В. Б. Численное решение некоторых классов двумерных сингулярных интегральных уравнений//Тр. XV междунар. симпозиума "Методы дискретных особенностей в~задачах математической физики".-Харьков-Херсон, 2011.-С. 108-111.
- Mikhlin S. G., Prossdorf S. Singular integral operators.-Berlin: Akademie-Verlag, 1986.-528 p.
- Гохберг И. Ц., Фельдман И. А. Уравнения в свертках и проекционные методы их решения.-М.: Наука, 1971.-352 c.
- Симоненко И. Б. Локальный метод в теории инвариантных относительно сдвига операторов и их огибающих.-Ростов-на-Дону: ЦВВР, 2007.-120 c.
- Михлин С. Г. Многомерные сингулярные интегралы и интегральные уравнения.-М.: Физматгиз, 1962.-256 c.
- Соболев С. Л. Введение в теорию кубатурных формул.-М.: Наука, 1974.-707 c.
- Партон В. З., Перлин П. И. Методы математической теории упругости.-М.: Наука, 1981.-688 c.
- Михлин С. Г., Морозов Н. Ф., Паукшто М. В. Интегральные уравнения теории упругости.-СПб: Изд-во СПбГУ, 1994.-272 c.
- Нуссбаумер Г. Быстрое преобразование Фурье и алгоритмы вычисления сверток.-М.: Радио и связь, 1982.-248 c.
- Оппенгейм А., Шафер Г. Цифровая обработка сигналов.-М.: Техносфера, 2009.-856 c.
- Vasilyev V. B. On certain continual and discrete onvolution operators//Proc. MATHMOD Vienna 09. 6th Vienna Conf. on Math. Modeling (February 11-13, 2009, Vienna University of Technology). Full Papers CD Volume/Eds. I. Troch, F. Breitenecker. Argesim Report \No 35.-P. 2616-2618.
- Гавурин М. К. Лекции по методам вычислений.-М.: Наука, 1971.-248 c.
Статья научная
