Приближенный метод определения моментов инерции тел с жидким наполнением

Движение твердого тела с полостями, целиком заполненными жидкостью, было впервые подробно исследовано Н.Е. Жуковским, который показал, что прямолинейное движение такого тела ничем не отличается от прямолинейного движения абсолютно твердого тела, масса которого равна сумме масс тела и жидкость.

- Вращательное движение твердого тела с полостями, целиком заполненными жидкостью, эквивалентно вращательному движению абсолютно твердого тела с некоторым приведенным или эквивалентным моментом инерции [Л].

Для тел, частично заполненных жидкостью, следуя Н.Е. Жуковскому, определение моментов инерции связано с отысканием функции г/, которая удовлетворяет внутри полости уравнению

Лапласа

V^O,

а на стенках полости и свободной поверхности - условиям би _ _

—= гхп, дп где г - радиус-вектор точки поверхности; п - единичный вектор нормали к поверхности.

Краевая задача (1) и (2) для потенциала скоростей г/ частиц жидкости соответствует слу чаю, когда свободная поверхность прикрыта крышкой, скрепленной со стенками полости. Эта функция определяется только геометрией полости и не зависит от времени. Она может быть оп ределена для полостей заданной формы раз и навсегда.

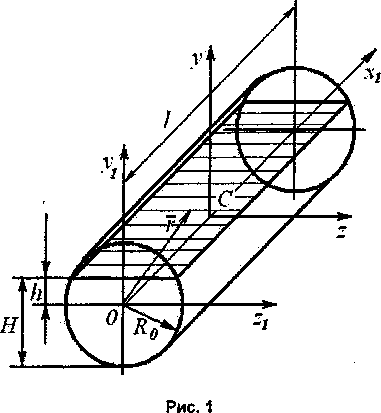
Рассмотрим движение цилиндрического бака в продольной плоскости (рис. 1) и определим момент инерции тела с жидкостью относительно оси Zj.

Момент инерции системы относительно данной оси будет складываться из переносного момента инерции

ЛХж=т№\(3)

где т - масса жидкости; Z/2 - расстояние до оси z, и собственного осевого момента инерции 7_0ж эквивалентного твердого тела относительно оси z

Аж = с /(grad И? dф.(4)

Ф Здесь ц = ц2+ху,(5)

где гармоническая функция г/., согласно формуле (2)

удовлетворяет граничным условиям:

6lfz                            Г 1 X 8Ч2

-2у на правом днище (х = —),

—- = 2 у на левом днище (х = —), —— бх                           2 бх

Расчет и конструирование

^- = 0 на боковой поверхности ( R = R_x), ^- = 0 на свободной поверхности ( у = h). 9R                                 8у

Отыскание функций z/z представляет большие трудности. Н.Е. Жуковский решил эту задачу для полностью заполненных полостей в форме прямоугольного параллелепипеда и круглого цилиндра. Для полостей сложной формы требуется применение численных методов.

В частном случае шаровой полости вращение твердого тела вокруг центра полости не вызывает движения идеальной жидкости (г/ = 0). Эквивалентное тело представляет собой в этом случае материальную точку, в которой сосредоточена вся масса жидкости.

В случае кубической полости с длиной ребра, равной а, приведенный момент инерции жидкости для оси, проходящей через центр полости, оказывается равным Л_Ож = 0,0261 т а².

Так как момент инерции куба равен та2 /в, то момент инерции эквивалентного тела со ставляет только 0,1565 момента инерции жидкости.

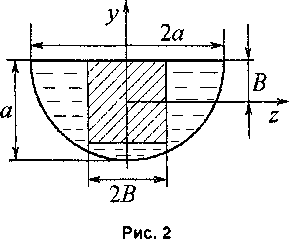
Эту особенность поведения жидкого объема во вращающейся полости будем называть свойством «невовлекаемости». На основании этого свойства можно получить простые формулы для вычисления приведенного момента инерции жидкости. Для примера рассмотрим полость в форме полушара радиуса а (рис. 2). Момент инерции полушара относительно оси z Jz = 0,25938ma2, где масса жидкости т = с Ip а3 (З- 2,0944 с а3.

Невовлекаемая часть объема жидкости (на рис. 2 эта часть заштрихована) равна 8S³, где В- 0,375а. Следовательно, невовлекаемая масса жидкости т* =0,421875 с а³ и масса эквивалентного тела составит т = 0,79857 .

Таким образом, момент инерции эквивалентного тела

J = 0.79857Л = 0,207133ша² •                    (6)

Н.Е. Жуковский, используя разложение функции г/ по сферическим функциям, вычислил эту величину с точностью до 0,0001 и нашел

Лж=0,2387„т2.                               (7)

Как видим, цена приближенного расчета составляет 13%.

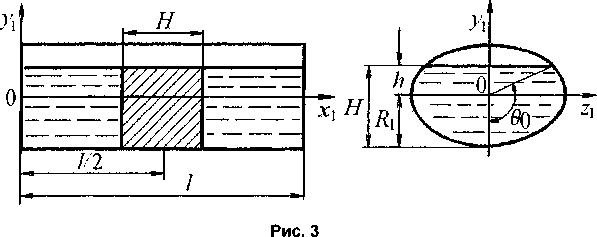
Пусть теперь требуется определить момент инерции цилиндрического бака с жидкостью (рис. 3) относительно оси z. Ограничимся определением присоединенного момента инерции /ж замкнутого объема жидкости относительно оси z. Момент инерции Лс будет складываться из переносного

3_Хж = cR_xG₆P ,4                                                             (8)

и собственного осевого Л_Ож моментов инерции.

В выражении (8) 7?] - характерный размер полости; G_o - безразмерная площадь поперечного сечения объема жидкости; I - I/R - относительная длина полости.

С учетом невовлекаемой части объема жидкости (на рис 3 эта часть заштрихована) собственный осевой момент инерции Л_Ож приближенно равен

J^pR^-H^U,                           (9)

где Н = h +1 - относительный общий уровень заполнения полости.

Подставляя (8), (9) в соотношение Л_ж = Л_Ож + Л_Хж , находим следующую формулу для приближенных вычислений J_ж:

Jж — с R_x J_ж,                                                                      (10)

где

7ж=П0(4/-^)72/12.

(И)

Павлюк Ю.С., Сакулин В.Д.

Применим формулу (И) для вычисления безразмерного присоединенного момента инерции жидкости в полости, имеющей форму кругового цилиндра. В этом случае

R_A= Ry, G_o = (2м₀ -sin 2w₀)/2, 2ы₀ -p + 2 arc sin h .

Следовательно, для круговых цилиндрических отсеков с жидкостью

7_Ж =(2У₀ -sin 20_о)(4/ -я)/²/24 .                                                (12)

Эта формула пригодна для расчета безразмерного момента инерции жидкости 1 _ж в полостях с относительной длиной 1>Н.

В частном случае, когда 7 = Н = 2 из (12) следует, что З_ж-2р.

Приведем несколько иллюстративных примеров использования формулы (12).

Для полости с параметрами I = 2, И = 0,98 применение вариационного метода с использованием шести сферических функций дает значение Л_ж =6,288. По формуле (12) получаем Л_ж = 6,294.

В таблице приведены некоторые результаты расчетов момента инерции Л_ж, полученные по формуле (12) и вариационным методом (последние величины расположены в знаменателе). Как видим, точность приближенной зависимости (12) вполне приемлема для практических расчетов.

Значения безразмерного момента инерции жидкости Эж в зависимости от относительной длины полости 7 и относительной глубины жидкости h

1	h =0	h =0,2	h =0,4	И =0,6	h =0,8	h =0,95
2	3,665/2,875	4,461/3,687	5,168/4,436	5,748/5,086	6,155/5,570	6,293/5,784
4	31,42/29,86	38,84/37,97	45,73/45,76	51,73/52,27	56,39/57,12	58,46/59,01
6	108,4/106,9	134,6/135,6	159,3/162,0	181,1/185,4	198,3/203,8	206,4/211,7
8	260,0/260,0	323,0/327,0	383,0/391,0	437,0/448,0	480,0/494,0	500,0/516,0
10	511,0/509,0	636,0/641,0	756,0/766,0	862,0/876,0	948,0/965,0	990,0/1011
12	886,0/895,0	1105/1119	1314/1341	1500/1536	1651/1695	1725/1770

Описанный подход можно легко распространить на объекты более сложной формы.