Прикладные и теоретические проблемы теории стабильности

Традиционное решение задач механики следует классической схеме: явление — модель — дифференциальное уравнение модели — решение уравнения — анализ решения. Предполагается, что решение уравнения описывает все свойства данной модели явления, следующие из уравнения. В тех случаях, когда результаты теоретических исследований не сходятся с экспериментом, исследователь уточняет или меняет модель, или уточняет решение. Однако, к сожалению, самым тщательным образом рассчитанные модели, учитывающие все тонкости явления, не дают стопроцентной гарантии надежной работоспособности системы при различных воздействиях и различных условиях. Конструкции, тщательно рассчитанные, могут разрушиться, механизмы неожиданно начинают давать сбой и так далее. Что является причиной необъяснимого поведения систем? На первый взгляд это непонятно, так как все мыслимые и немыслимые расчеты сделаны, внешние воздействия учтены, проверены и перепроверены! Напрашивается вывод, что есть еще что-то такое, что исследователь не заметил, но что, возможно, уже имеется в модели и уравнениях, её описывающих. Теория стабильности выдвигает и частично обосновывает гипотезу, что белые пятна не в указанной цепочке (явление — ... — анализ решения), а вне её. В этой цепочке есть неисследованная боковая ветвь: дифференциальное уравнение модели — свойства самого уравнения. Это направление не исследуется, так как обычно предполагается, что решение уравнения описывает все то, что может дать данное уравнение явления. Возможно, уравнение имеет еще какие-либо свойства, непосредственно с решением не связанные, но содержащие механический смысл, соответствующий в какой-то мере критическим ситуациям.

Механическое движение твердых тел, деформирование упругих и неупругих сред и конструкций описывается дифференциальными уравнениями. Для задач о движении материальной точки или тела необходимо ставить какие-то начальные условия, или какие-то условия на характеристики этого движения, позволяющие найти константы интегрирования. Принят наиболее естественный вариант: в некоторый момент времени, например, при t = 0 , известны координаты точки и её скорость. Отсюда можно получить зависимость координат точки во все последующее время. Число начальных условий равно порядку дифференциального уравнения. Но ничто не запрещает поставить условия и на ускорение или даже высшие производные — третьи, четвертые и более высокие порядки. Такую начальную задачу будем называть обобщенной задачей Коши [1]. В этом случае с помощью уравнения движения можно найти значения начального положения и скорости, выразив их через заданные высшие производные. Здесь мы и подходим к сути теории стабильности. Процедура выражения функции и скорости через высшие производные в некоторых случаях может не состояться ! Эти случаи являются особыми точками начальной задачи и называются потерей стабильности процесса, или, иначе, нестабильностью. Имеем, например, дифференциальное уравнение x + ( a - t ) x = 0 , где точка над символом означает производную по времени x = dx ( t )/ dt , a — некоторое число. Если поставить условие на скорость x ( 1 ₀ ) = v ₀ , то найти x ( t ₀ ) можно лишь при t = a . Таким образом, в предлагаемом определении, значение t = а является точкой нестабильности (особой точкой) процесса. В рамках одной теории будем различать две постановки: анализ стабильности процесса и анализ стабильности возмущенного движения (или процесса).

Второй случай относится в большей степени к процессам, описываемых нелинейными уравнениями. Поясним это на примере [2]. Уравнение прямолинейного движения точки массой m под действием в общем случае переменной силы F имеет вид mv = F, где v(t) — скорость точки. Пусть сила зависит от скорости: F = -av - bI v, где a и b — некоторые константы. Для скорости точки имеем, таким образом, обыкновенное дифференциальное уравнение первого порядка mV v + av2 + b = 0.                                   (1)

Рассмотрим малое отклонение от основного процесса, выбрав условно за основной процесс решение уравнения при определенном заданном начальном условии на v ( t ) . В результате возмущения функция v ( t ) и её скорость v ( t ) приобретут приращения A v , A v . Линеаризуя (1), получаем

mvAv + (mv + 2 av )A v = 0.

В те моменты времени, когда скобка при A v обращается в нуль, связь приращений A v и A v

v ₎

^Л v    ) + (2 a I m ) v^

вырождается. Равенство знаменателя в этом выражении соответствует нестабильности возмущенного процесса. Так как из уравнения движения следует v = - (a v+bI v )l m, то нестабильность наблюдается при совершенно определенной скорости движения, не зависящей ни от массы, ни от начальных значений v = Vb I a.                                            (2)

Если из решения уравнения движения известна функция v ( t ) ,то из (2) можно найти значение t , при котором малые или даже как угодно малые возмущения A v скорости должны соответствовать неограниченно большим возмущениям ∆ v . Безусловно, такая особенность что-то значит для основного процесса. Однако проявляется это не так явно, как в задачах устойчивости, так как здесь требуется возмущение совершенно определенного вида, да еще и приложенного в соответствующий момент, но пренебрегать этим фактом в расчетах нельзя.

Приведем две математические модели, иллюстрирующие проявление нестабильности в двух, в общем-то совершенно разных по природе, механических процессах.

1. Модель 1. Выпучивание стержня при ползучести

Проблема поиска критического времени конструкций в условиях ползучести, связанная с важными технологическими задачами ядерной энергетики (стержневые элементы реакторов), космонавтике и авиации (сжатые оболочки двигателей при высоких температурах), широко обсуждалась в середине прошлого века [3-7]. Здесь непосредственное применение теории устойчивости либо не дает объективных решений, привязываясь к величинам начальных несовершенств, величины которых найти затруднительно или невозможно, либо просто дает тривиальный вывод о неустойчивости любой конструкции в условиях ползучести. В [8] для решения этой задачи привлекается теория стабильности.

Найти для примера точки нестабильности второго порядка и критическое время продольно сжатого постоянной силой P , шарнирно опертого стержня из реологического материала

Р Р “ = f (о),                                         (3)

p = е - о I E — деформация ползучести, а — константа материала (коэффициент упрочнения), f ( о ) — заданная функция, определяющая зависимость деформации ползучести от уровня напряжений (степенная, гиперболический синус и другие). Длина стержня l , рисунок 1.

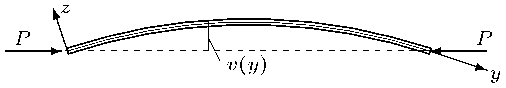
Рис. 1. Выпучивание стержня

Рассмотрим малое отклонение стержня от прямолинейного состояния. Деформации в изогнутом стержне получают приращения. Ось y материальной системы координат (“вмороженной” в тело) направим по срединной линии стержня, ось z — по нормали к ней. На основании гипотезы плоских сечений

A e = A e о + z A v , yy ,                                        (4)

где A e — приращение осевой деформации на расстоянии z от срединного сечения, A e _о — приращение деформации срединного сечения, равные нулю, если в результате возмущения нагрузка на стержень не изменилась, A v — приращение прогиба стержня, A v , yy — вторая производная приращения прогиба по осевой координате y . Умножаем (4) на z и интегрируем по площади сечения. Так как приращение деформации срединной поверхности стержня A e _о не зависит от z , а для симметричного относительно оси y сечения статический момент zdF равен нулю, то получим                                                        ^F

J” A E zdF = J A v , yy ,                                      (5)

F

J = f z2dF — момент инерции поперечного сечения стержня. Уравнение равновесия (моментов) F отсеченной части стержня относительно точки на срединной линии сечения дает

J A a zdF = - P A v ,                                 (6)

F где P = f dF — нагрузка, действующая на стержень в продольном направлении. В случае линейной упругости приращения напряжений и деформаций связаны законом Гука

A a = E A e .

Умножим это уравнение на z и проинтегрируем по площади F . Интегралы от z ∆ ε и z ∆ σ выразим через (5) и (6). Получим

EJ A v , yy + P A v = 0.

Форму прогиба выберем в виде, удовлетворяющем условию шарнирного опирания по концам ( A v = 0 при y = 0 и y = 1 ):

A v = u sin ky ,                                        (7)

где k — параметр волнообразования, k = m ₁ n / 1 , m ₁ — число полуволн по длине стержня. Условия отсутствия моментов на опорах A v , yy = 0 при этом удовлетворяются автоматически. Получим

u sin ky (-k2 EJ + P) = 0.

Из условия u = 0 найдем критическую нагрузку (формула Эйлера) P ₀ = k ² EJ . Соответствующее напряжение обозначим a ₀ = k ² EJ / F . Пусть стержень выполнен из реологического материала (3). В результате отклонения от прямолинейного положения приращения напряжений и деформаций ползучести, согласно (3), удовлетворяют соотношению

A p p ^а + a A pp p ^{а 1} = f '( a ) A a ,

где p , p ) и a относятся к оси стержня, а A p , A p ) и A a означают малые приращения соответствующих величин по толщине стержня.

Введем обозначения безразмерного напряжения, отнесенного к эйлеровому значению ш = a / a ₀ , и параметра, зависящего только от напряжений,

Z = (f 7 f) E ш/(1 - ш).

Из (6) с учетом выражения A p = A e - A a / E и уравнения (5) следует

У ApzdF=

- P A v / E + J A v , yy .

Умножим (8) на z и проинтегрируем по площади F :

p^a J A pzdF + a pp^{a 1} У A pzdF = f '( a ) j

A a zdF .

Разделим обе части уравнения на p ^α и, учитывая, что величины без значков ∆ не зависят от z , с помощью (6) получим отсюда

J Av , yy + P A v / E + p ( P A v I E + J A v , yy ) a I p = - P A vf ‘ p ^{- a} .                 (10)

Если выбирать форму прогиба в виде синусоиды (7), то из (10) следует, что скорость прогиба должна иметь такой же вид A ) = u sin ky , при этом A ) , yy = - k ² u sin ky . Заменив в правой части p ^a на f I p , получим

( - k ² J + P / E ) u + p ( P / E - k ² J ) и a / p = - Pup ) f ' / f .

Эйлерова нагрузка упругого стержня P ₀ = EJk ² . Делим последнее равенство на P / E - k ² J = P о ( ш - 1)/ E :

U + up) (a/ p - (f'/f)Eш/(1 - ш)) = 0.

Пользуясь обозначением (9), получим уравнение для u :

Up + up ( a - p Z ) = 0.

Точка нестабильности второго порядка соответствует вырождению связи приращений прогиба, скорости прогиба с заданным (как угодно малым) приращением ускорения [8]. Искусственно поднимаем порядок (11), дифференцируя его по времени. Помня, что по условию задачи нагрузка постоянная, Z = const, а деформация ползучести удовлетворяет (3), после некоторых преобразований, получим

Up2 + Upp(a - pZ) + up)2a(pZ - a - 1) = 0.                        (12)

Введем обозначение £ = p Z . Систему (11), (12) запишем в матричном виде

AJJ = У ,                                          (13)

где

[ p(a - ^)[ - a p^( a - ^ +1)

• (p,) b jj=1u bv=1 o.. 1. p p (a - ^) ]       [ u ]       [ p2 и J

Равенство нулю определителя матрицы A соответствует нестабильности второго порядка:

p ^2 - 3 p a^ + p a (2 a +1) = 0.

Находим корни уравнения

3 a ± V a2 - 4 a2

Это решение существует при a >  4 . Для того чтобы найти критическое время, проинтегрируем (3) при постоянных нагрузках и нулевых начальных условиях:

t = p a+1/(( a +1) f).

Соответствующую деформацию ползучести подставим сюда из (15), взяв меньшее значение:

3 a - V a ² - 4 a

p =

2Z

С увеличением нагрузки критическое время уменьшается. При P ^ P ₀ параметр Z (9) стремится к бесконечности, а критическое время к нулю, что соответствует физическому смыслу задачи. Эйлерова нагрузка приводит к мгновенному выпучиванию стержня.

Аналогично можно получить точки нестабильности других порядков. Если точка нестабильности второго порядка является корнем полинома (14), который обозначим за Q2, для точки третьего порядка (задается возмущение третьей производной, а прогиб, скорость и ускорение прогиба неограниченно растут в момент возмущения) найдем полином Q3 как определитель матрицы 3 х 3. Выпишем первые четыре полинома:

Q1 - £ — а,Q2 — £2 - 3£а + а(2а +1),

Q3 - £3 - 6а£2 + а(4 +11 а)£ — а(2а + 1)(3а + 2),Q 4 — £4 — 10 а£3 + 5 а (2 + 7 а) £2 — 5 а (2 а + 1)(5 а + 2) £++ а (2 а + 1)(3 а + 2)(4 а + 3).

Имеется дифференциальная рекуррентная зависимость

Qn — Qn—1(£ + 1 — N(1 + а)) + QN—1 £, N — 2,3,4.....

где штрихом обозначена производная по ξ . Корни полиномов для определения точек нестабильности порядков 1-7 в зависимости от коэффициента упрочнения α изображены на рисунке 2. Полиномы нечетных порядков имеют корни для любых α , четных — при достаточно больших коэффициентах упрочнения. Для построения кривых в Maple не потребовалось искать корни, в этом случае оказался особо удобным оператор implicitplot для изображения неявных функций. Точка нестабильности первого порядка £ — а совпадает с известным (полуэмпирическим) критерием Работнова-Шестерикова [4, 5], выделяющим критическую точку по знаку скорости роста прогиба после возмущения.

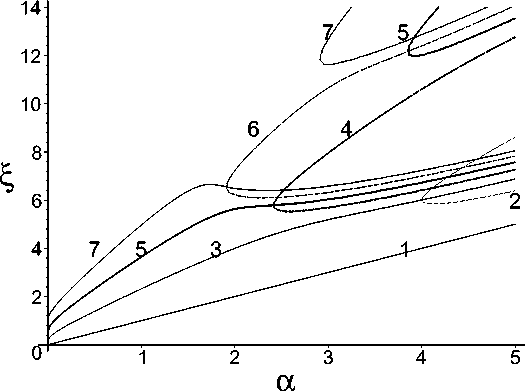
Рис. 2. Критические значения ξ при разных коэффициентах упрочнения

—m 2 g cos ф — MI r — 0, где mS — m 1 + m2 + m3.

Уравнение (16), описывающее движение системы, нелинейное. Интересно проанализировать связь приращений функций, описывающих движение системы и их производных, и выявить их особые точки. Под особыми точками здесь мы будем понимать точки нестабильности,

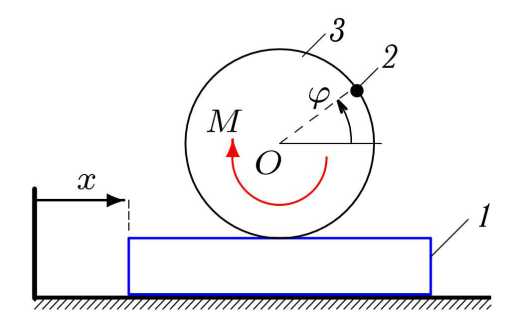
Рис. 3. Механизм с двумя степенями свободы

то есть те значения параметров системы, при которых связь приращений высших и низших производных процесса вырождается. Будем рассматривать возмущения (малые приращения) функции ф . Пусть задано приращение Д ф и вторая производная приращения Д ф . Согласно определению [1] это соответствует поиску особой точки порядку 0/2. Уравнение (16) перепишем в виде

ф( a + 2 b 2 sin ф + b 1 cos2 ф) + ф2( b 2 - bisin ф )cos ф + c cos ф + M = 0,           (17)

где a = r 2(4 m 1 m 2 + m 3(3 m 1 + 3 m 2 + m 3))/(2 mS), b 1 = r 2 m 2/ ms, b 2 = r 2 mi m 2/ ms, c = m 2 gr.

После линеаризации это уравнение в приращениях имеет вид

A 1,0 ^Д ф + A 1,1 ^{Д ф} + A 1,2 ^{Д ф} + A 1,3 ^{Д ф} = °                         ⁽¹⁸⁾

где A ₁ , ₃ = 0 . Для замыкания этого уравнения на третью производную приращения поднимем его порядок, продифференцировав по времени

A 2,0 ^Д ф + A 2,1 ^{Д ф} + A 2,2 ^{Д ф} + A 2,3 ^{Д ф} = °

где A 1,1 = 2ф(b2 - b 1sinф)cosф, A2,3 = 2b2sinф + b 1cos2 ф + a.

Для того, чтобы свести обобщенную задачу Коши к классической, необходимо выразить первую производную через заданные функции. Систему (18)-(19) перепишем в матричном виде

[ A 1,1

A 2,1

A 1,3

A 2,3

1 Г Д (ф 1 = Г A 1,0 Д ф Д ф + A 1,2 Д <ф Д ф         A 2,0 Д ф Д ф + A 2,2 Д ф

Особая точка процесса в приращениях (аналог устойчивости) соответствует равенству нулю определителя

A 1,1 A 1,3

det                  = A 2,3 A 1,1 — A 1,3 A 2,1 =

A 2,1 A 2,3

= 2ф(2b2 sinф + b 1 cos2 ф + a) (b2 - b 1 sinф) cos ф = 0.

Легко показать, что уравнение A ₂ , ₃ = 2 b ₂ sin ф + b ₁ cos ² ф + a сводится к квадратному и корней не имеет. Имеются три возможных точки нестабильности

cosф = 0, (ф = 0, sinф = b2/b 1 = m 1/m2.

При этом корень последнего уравнения существует только при m ₁ <  m ₂ .

Что происходит с системой в особой точке? Уравнения показывают, что при как угодно малых возмущениях функции и её ускорения в этот момент скорость возмущения и третья производная могут неограниченно расти. Такие ситуации в реальных объектах могут соответствовать различного рода неоднородностям и срывам. В поршневых системах это приводит к заклиниванию механизма [10]. Возможно, в реальной ситуации этот момент будет несколько смягчен за счет проскальзывания трущихся частей и неточности попадания в особую точку. В любом случае, особая, в таком понимании, точка имеет смысл только при наличии соответствующего возмущения. В рассмотренном случае это возмущение угла и углового ускорения. При отсутствии возмущения механизм минует это состояние без каких-либо последствий.

Также можно исследовать и стабильность рассмотренной механической системы и для других порядков: 0/3, 1/2, 1/3. При задании приращения и его скорости (порядок 0/1) особых точек в системе нет (классическая задача Коши).

Аналогичные проблемы динамики нелинейных систем исследовались в нелинейных задачах резанья металлов [11-14], в исследованиях особенностей обыкновенных дифференциальных уравнений [15-23]. Постановка задачи теории стабильности возможна не только при исследовании динамических или квазистатических процессов, но и плоской задаче теории упругости с уравнениями в частных производных [24].

Заключение

Явление нестабильности присуще исключительно нелинейным процессам и состояниям [2]. Процедура выявления особых точек в смысле нестабильности отработана и, несмотря на очевидные математические трудности, характерные для любых нелинейных задач, не имеет принципиальных ограничений. Интересно отметить, что во всех решенных задачах по этой теме применялись аналитические методы с применением систем компьютерной математики. Численные методы, развитые для решения уравнений, а не исследование постановок начальных задач, пока еще не применялись. Численные методы для выявления условия обращения в нуль определителя менее эффективны, чем аналитические. Другой особенностью задач стабильности является некоторая неопределенность закритического поведения системы после достижения особой (в смысле нестабильности) точки, что вызывает критику [25]. Для решения послекритического состояния или движения системы необходимо рассмотреть уравнения типа (18)-(19) с учетом квадратов приращений функции и её производных. Это составит материал для дальнейших исследований.