Приложение тройных интегралов
Автор: Гильманова Г.Р.
Журнал: Экономика и социум @ekonomika-socium
Рубрика: Современные науки и образование
Статья в выпуске: 9 (28), 2016 года.
Бесплатный доступ
Статья посвящена приложению тройных интегралов. В статье рассматриваются их геометрические и физические приложения. Представлены формулы для решения тройных интегралов с разными способами, а также решены некоторые задачи.
Тройные интегралы, геометрические приложения, физические приложения, объем тела, инерция
Короткий адрес: https://sciup.org/140121467
IDR: 140121467
Текст научной статьи Приложение тройных интегралов
Геометрические приложения тройных интегралов
Геометрическое приложение - вычисление объема любого пространственного тела.
Объем тела U в декартовых координатах Oxyz выражается формулой у=Kf ^х^у^-и
В цилиндрических координатах объем тела равен
У = Iff P^pdpdz
В сферических координатах, соответственно, используется формула
V = J'£f Р^п&^Р^Ф^-
<7
Пример
Найти объем шара x2 + y2 + z2 ≤ R2.
Решение.
Вычислим объем части шара, расположенной в первом октанте (x ≥ 0, y
≥ 0, z ≥ 0), и затем умножим результат на 8. Получаем
% 5 %
и w ООО
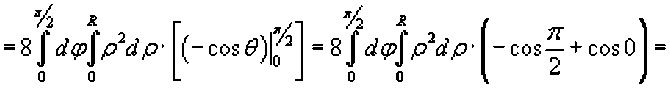
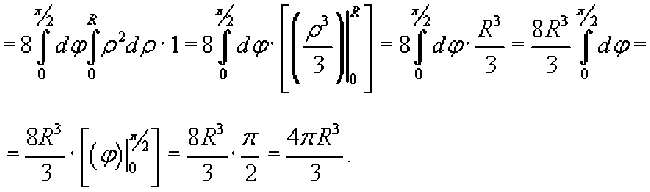
В результате получена известная формула для объема шара радиусом R. Физические приложения тройных интегралов
Масса и статические моменты тела
Пусть тело занимает объем U и его объемная плотность в точке M(x,y,z) задана функцией ρ(x,y,z). Тогда масса тела m вычисляется с помощью тройного интеграла:
т = ^^’ y^}dxdydz.
D’
Статические моменты тела относительно координатных плоскостей Oxy, Oxz, Oyz выражаются формулами
^^PPP^t^X2)^^- M^ = ^xp[x,y,z}dxdydz, Мкг = ^yp(x,y,z)dxdydz.
и и и
Координаты центра тяжести тела вычисляются по формулам:
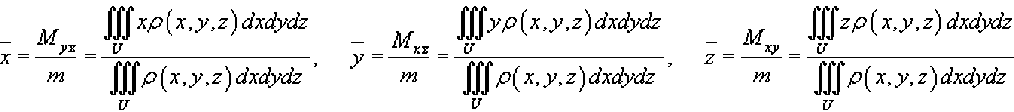
Если тело является однородным с плотностью ρ(x,y,z) = 1 для точек M(x,y,z) в области U, то центр тяжести тела зависит только от геометрии тела и называется центроидом.
Моменты инерции тела
Моменты инерции тела относительно координатных плоскостей Oxy, Oxz, Oyz определяются выражениями
^rjJppf^J^^^A 4z = JJ^M*’^)^^’ /7г = JJp2p(*,;n,z)^^ и и и а моменты инерции тела относительно координатных осей Ox, Oy, Oz вычисляются по формулам
4 = /Ж^ + z2^p{x,y,z)dxdydz, 1у = ДДх2 + z2^p(x,y,z)dxdydz, 4 = ДИ*2 + y2)p(x,y,z)dxdydz.
Как видно, справедливы соотношения
1=1+1 I =1 +1 I =1 +1
Моментом инерции тела относительно начала координат называется интеграл
4 = /Ж^ ^"^ +^'^p(x,y,z')dxdydz
Момент инерции относительно начала координат можно выразить через моменты инерции относительно координатных плоскостей:
^0 = Цу+ ^1+^г
Тензор инерции
Используя рассмотренные выше 6 чисел Ix, Iy, Iz, Ixy, Ixz, Iyz, можно составить так называемую матрицу инерции или тензор инерции тела:
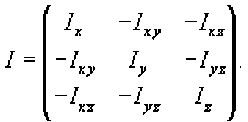
Данный тензор является симметричным, и, следовательно, его можно привести к диагональному виду при определенном выборе осей Ox', Oy', Oz'. Значения диагональных элементов (после приведения тензора к диагональному виду) называются главными моментами инерции, а указанные направления - собственными векторами или главными осями инерции.
Если тело вращается вокруг оси, не совпадающей с главной осью инерции, то оно будет испытывать вибрации при высоких скоростях вращения. Поэтому, при конструировании таких устройств необходимо, чтобы ось вращения совпадала с одной из главных осей инерции. Например, при замене шин автомобиля проводится их балансировка: небольшие грузики добавляются к колесам, чтобы обеспечить совпадение оси вращения с главной осью инерции и исключить вибрации.
Гравитационный потенциал и сила тяготения
Ньютоновым потенциалом тела в точке P(x,y,z) называется интеграл
^(^.г)-Jfp(гл.^^^.
Г =-^-хр^гУ?^^
где ρ(ξ,η,ζ) - плотность тела, и .
Интегрирование выполняется по всему объему тела. Зная потенциал, можно вычислить силу притяжения материальной точки массы m и заданного распределенного тела с плотностью ρ(ξ,η,ζ) по формуле
F = ~Gm grad a, где G - гравитационная постоянная.
Пример
Найти массу шара радиуса R, плотность γ которого пропорциональна квадрату расстояния от центра.
Решение.
По условию, плотность γ задана соотношением γ = ar2, где a - некоторая постоянная, r - расстояние от центра. Массу шара удобно вычислить в сферических координатах:
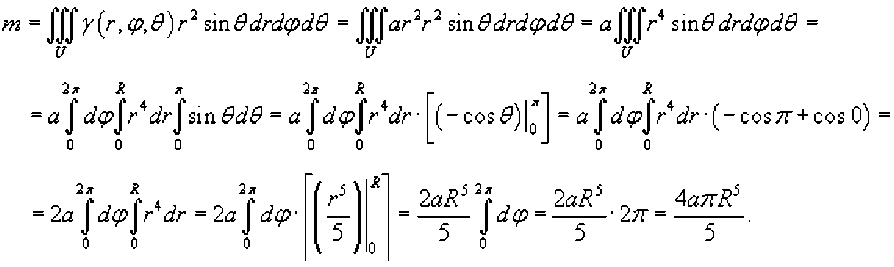
Список литературы Приложение тройных интегралов
- Фихтенгольц Г.М. «Курс дифференциального и интегрального исчисления» (II том) -Москва, 2013.
- Пискунов Н.С. «Дифференциальное и интегральное исчисления» (I том) -Москва, 2015.
- Эрмит Ш. «Курс анализа» -Москва, 2014


