Применение алгоритма муравьиной оптимизации для построения оптимальной траектории скважины

Оптимизация траекторий скважин

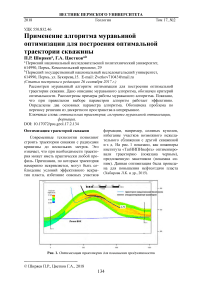
Современные технологии позволяют строить траектории скважин с радиусами кривизны до нескольких метров. Это означает, что при необходимости траектория может иметь практически любой профиль. Причинами, по которым траектория намеренно искривляется, могут быть соблюдение условий эффективного вскрытия пласта, избегание опасных участков формации, например, соляных куполов, избегание участков возможного нежелательного сближения с другой скважиной и т. д. На рис. 1 показано, как инженеры института «ТатНИПИнефть» оптимизировали траекторию (показана черным), предложенную заказчиком (показана синим). Данная оптимизация была проведена для повышения нефтеотдачи пласта (Хабирова Л.К. и др., 2015).

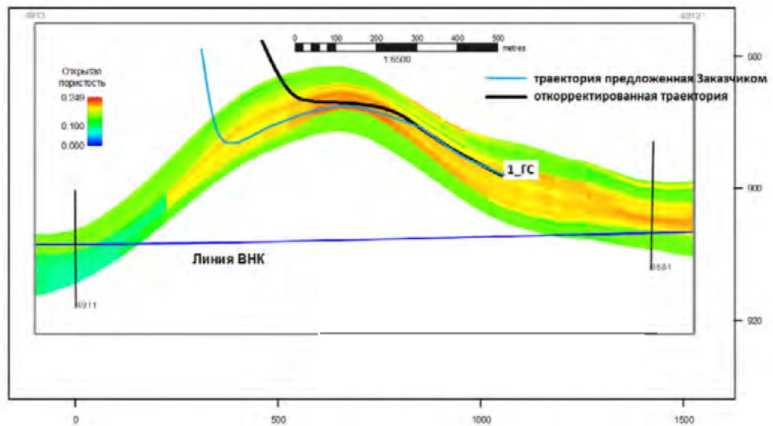
Рис. 1. Оптимизация траектории для повышения продуктивности

Существует множество других критериев оптимизации траектории скважин: по длине скважины, по минимальной стоимости, по минимальным рискам аварий, по минимальному ущербу природе, по максимальной скорости бурения, по наиболее простой для проводки траектории ( Camron, 2008, Али. и др., 2005) .

Алгоритм муравьиной оптимизации

В данной статье рассматривается оптимизация по максимальной скорости проводки скважины. Комплексным показателем, характеризующим насколько форма- ция тяжела для бурения, является буримость. Таким образом, буримость будет характеризовать, насколько быстро можно проводить скважину в той или иной области формации при неизменных технологических параметрах (Стрик, 2004).

Для решения задачи оптимизации рассматриваемая область формации разбивается на элементарные объемы, каждому из которых ставится в соответствие значение буримости (см. рис. 2). После этого для нахождения оптимальной по буримости траектории применяется алгоритм муравьиной оптимизации.

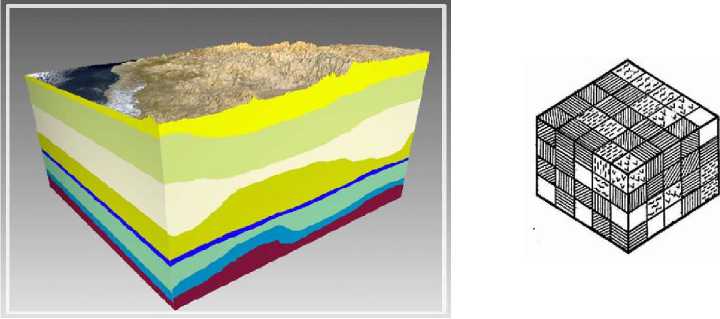
Рис. 2. Буримость породы

Алгоритм муравьиной оптимизации – эвристический оптимизационный алгоритм, основанный на поведении муравьев в природе. Муравьи, ища пути к источникам пищи, способны помечать найденные пути, причем более короткие (более выгодные) способны отличать от более длинных (менее выгодных). Чтобы пометить путь, ведущий к пище, муравьи используют феромон – пахучее вещество, вырабатываемое ими. Данная система является адаптивной, т. е. при изменении расположения источников пищи муравьи постепенно перестроят свои пути.

В применении к оптимизации траектории скважины природный муравьиный алгоритм используется следующим образом:

• 1.    Муравьи начинают поиск из начальной точки.

• 2.    На каждом шаге каждый муравей выбирает следующий элементарный объем (куб) для шага (см. рис. 3).

• 3.    Муравьи повторяют п. 2 пока либо не дойдут до коллектора, либо не зайдут в тупик.

• 4.    После того, как муравьи завершили движение (либо нашли траекторию, либо оказались в тупике), найденные траектории оцениваются. На найденные траектории наносится феромон в соответствии с тем, какую суммарную буримость они имеют: чем меньше суммарная буримость, тем больше феромона наносится.

• 5.    Повторяется основной цикл алгоритма по числу итераций. Решением явля-

• ется лучшая траектория, найденная за все время поисков.

Рис. 3. Выбор следующего куба для шага

Возможны различные варианты выбора следующего куба: случайный выбор, выбор, соответствующий наиболее сильно рекомендуемому кубу, выбор по направлению к цели. Возможны и другие варианты. На рис. 3 предполагается, что мура- вей находится в красном кубе, а остальные раскрашенные кубы рассматривает как возможное продолжение траектории.

Пункты 1) — 4) относятся к основному циклу алгоритма

Представленная последовательность действий отображает все этапы работы муравьиного алгоритма.

Муравьиный алгоритм содержит большое число параметров, но основными параметрами являются два: число муравьев и число итераций основного цикла.

Полученные результаты

При проведении экспериментов были получены следующие результаты.

На рис. 4 показан тестовый пример, в котором отмечены два тяжело буримых участка (выделены розовым). Пласт-коллектор выделен коричневым.

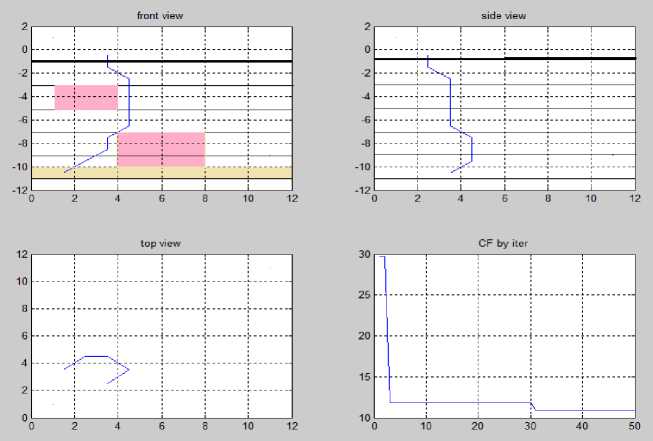
Рис. 4. Тестовый пример с двумя тяжело буримыми участками

На левом верхнем рисунке показан вид траектории спереди, на правом верхнем — сбоку, на левом нижнем — сверху, на правом нижнем — убывание (улучшение) критерия оптимальности по итерациям основного цикла.

Видно, что муравьиный алгоритм нашел траекторию, которая избегает тяжело буримых участков.

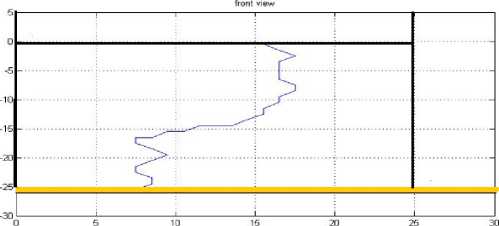
Другие примеры построенных муравьиным алгоритмом траекторий показаны на рис. 5 и 6.

На них сверху показан вид траектории спереди, а снизу — улучшение критерия оптимальности по итерациям основного цикла.

Во втором и третьем тестовых примерах не было четко выделенных участков с высокой буримостью, буримость была распределена случайным образом. Траектория, полученная в третьем примере, содержит два прямых участка и является удобной для реализации. Траектория, полученная во втором примере, содержит намного больше поворотов и углов, что делает ее сложной для реализации.

Кроме того, алгоритм может найти гораздо худшее решение, чем то, которое сложно реализовать — гарантированно неоптимальное. На рис. 7 изображена неоптимальная траектория, найденная алгоритмом. Видно, что траектория пересекает саму себя. Причиной этого является не- верный выбор параметров алгоритма, а именно слишком малое максимальное число итераций. Однако с увеличением числа итераций алгоритм способен находить оптимальные траектории.

CF bj iter

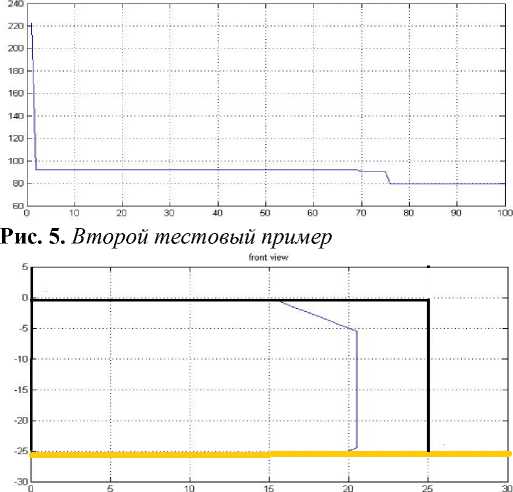
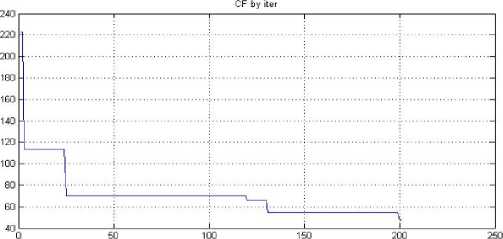
Рис. 6. Третий тестовый пример

После получения траектории в дискретном пространстве встает вопрос о том, как перенести ее в непрерывное пространство, поскольку невозможно и не нужно строить кусочно-непрерывную тра- екторию. Один из вариантов – скругление углов. В этом случае траектория станет гладкой и реализуемой. Второй вариант – сопряжение прямолинейных участков клотоидами (см. примеры клотоид на рис. 8).

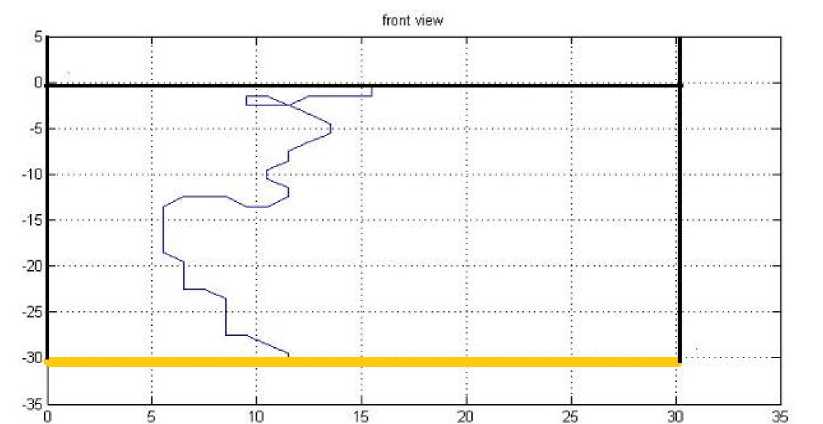
Рис. 7. Неоптимальная траектория

Рис. 8. Примеры клотоид

В работе Аl–Bajalan (2015) показано, что сопряжение дугами окружности клотоидами эффективнее, чем сопряжение дугами окружности.

Заключение

• 1.    Алгоритм муравьиной оптимизации можно использовать для построения траекторий скважин.

• 2.    При правильном выборе параметров алгоритм находит хорошее решение.

• 3.    Алгоритм находит решение в дискретном пространстве, а применять решение нужно в непрерывном. Поэтому необходим способ переноса решения в непрерывное пространство, в частном случае — интерполяция.