Применение алгоритмов построения выпуклой оболочки при анализе изображений микроструктуры металла

Бактимиров Линар Шамилевич, аспирант.

E-mail: l.biktimirov@ulstu. ru направлении внутритрубного воздействия [2].

Алгоритмы выделения выпуклой оболочки. Известны работы, в частности [1, 2], в которых предложены алгоритмы нахождения на металлографических изображениях некоторых микроструктурных параметров, например, таких как зернистость и общее отношение феррита к перлиту. Однако для получения большей информации о микроструктуре металла целесообразно исследование более «тонких» характеристик, таких, как параметры вытянутости пятен и вектор направленности зерен перлита. В простейшем случае среднюю вытянутость можно охарактеризовать параметром:

к выт

А , общ

N

Z A n k n n = 1

,

и среднюю направленность вектора перлитных

пятен:

—— kнапр

А , общ

N

Z( aa,)

n = 1

где An - площадь, kn - коэффициент вытянутости (один из примеров конкретизации этого понятия приведен ниже), an - вектор направленности n- го пятна, n = 1, N; Аобщ - общая площадь учитываемых пятен.

Из выражений (1) и (2) видно, что для оп-^— ределения квыт и кнапр необходимо найти коэффициент вытянутости и вектор направленности ддя всех N пятен, имеющихся на изображении. Исследования показали [3], что с точки зрения быстродействия и устойчивости оценок при решении задачи оценивания параметров вытянутости и угла

направленности изображения зерна перлита перспективным является подход, основанный на адаптивной псевдоградиентной адаптации [4]. Однако применение псевдоградиентного алгоритма оценивания указанных параметров эффективно только, если исследуемые перлитные пятна представлены их выпуклыми оболочками (ВО) (рис. 1, где ( x 0 , y o ) – центр тяжести пятна). Выпуклую оболочку пятна на плоском изображении можно определить как наименьший выпуклый многоугольник S, такой, что все точки пятна находятся либо на границе S, либо в его внутренней области [3]. Области, находящиеся между изображением пятна и его ВО, называют заливами.

Таким образом, параметры перлитных пятен можно найти в два этапа: построение выпуклой оболочки перлитных пятен и оценивание параметров k n и ^a n с помощью псевдоградиент-ных алгоритмов. Известно много алгоритмов выделения ВО, например алгоритм Чана, Киркпатрика, Мелькмана [5], но наибольшую распространенность получили алгоритмы Грэхема [6], Джарвиса [7] и так называемый алгоритм «быстрой выпуклой оболочки» (БВО) [8]. Рассмотрим их эффективность для рассматриваемой задачи.

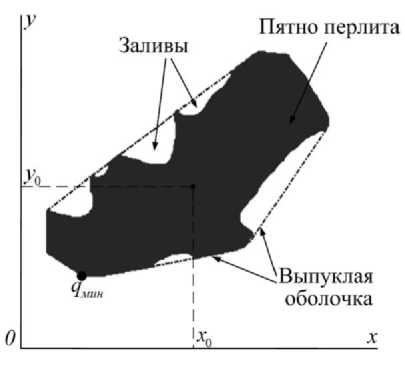
Рис. 1 . Пример перлитного пятна и его выпуклой оболочки

Алгоритм Грэхема состоит из следующих основных этапов:

• 1)    Нахождение минимальной точки объекта ( q мин ) (минимальная точка объекта определяется из условия минимального значения по оси ординат, а если таких точек несколько, то выбирается та, у которой значение по оси абсцисс наименьшее).

• 2)    Сортировка точек границ объекта в порядке возрастания полярного угла, измеряемого против часовой стрелки относительно точки q мин

(если полярные углы нескольких точек совпадают, то из них выбирается одна, наиболее удалённая от q мин ).

• 3)    Обход Грэхема (в основе которого лежит понятие «левого» и «правого» углов [6]), в результате которого выделяются точки, являющиеся вершинами ВО.

• 4)    Соединение найденных вершин.

Пример, демонстрирующий принцип работы алгоритма Грэхема, приведен на рис. 2, где q i – потенциальная точка, q тек – текущая точка, проходящая проверку на «правый» угол, q тек -1 – точка, состоящая в стеке перед проверяемой точкой, р i – точки выпуклой оболочки исследуемого объекта. Как видно из рис. 2, вершины ( q 4 , q 6 , q 7 ), не прошедшие проверку на «правый» угол, не являются вершинами ВО. Вычислительная сложность алгоритма Грэхема не зависит от количества найденных вершин и пропорциональна q log( q ), где q – количество внешних точек пятна .

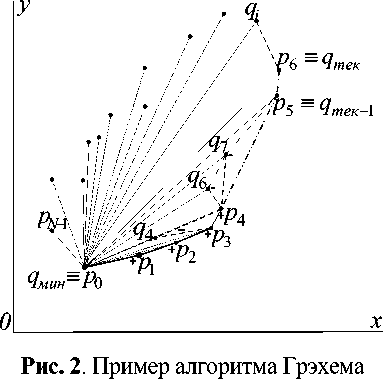
Алгоритм Джарвиса [6] (также известный как алгоритм «упаковки подарка») по сравнению с алгоритмом Грэхема является более простым и наглядным, и состоит из следующих основных этапов:

• 1)    Нахождение минимальной точки объекта q мин (аналогично алгоритму Грэхема).

• 2)    Обход Джарвиса [7], который выделяет точки выпуклой оболочки.

• 3)    Соединение найденных точек.

Пример, иллюстрирующий принцип обхода Джарвиса, показан на рис.3, где qi – граничные точки исследуемого пятна; pтек – текущая точка обхода Джарвиса, рсл – новая точка обхода Джарвиса, найденная на основе предыдущий по минимуму угла между векторами l и направлением ртек – рсл. Вычислительная сложность алгоритма Джарвиса, в отличие от алгоритма Грэхема, зависит от количества вершин многоугольника (пятна) и пропорциональна qh, где h – количество общих точек пятна и его выпуклой оболочки, что в худшем случае составляет q2.

тельная сложность алгоритма слагается из сложности построения все подмножеств.

Рис. 3 . Пример работы алгоритма Джарвиса

Рис. 4 . Пример работы алгоритма БВО

Алгоритм БВО состоит из следующих основных этапов:

• 1)    Выбор двух крайних точек пятна – левой L и правой R, являющихся вершинами ВО. Выбор точек пятна, имеющих наибольшее и наименьшее значение по оси абсцисс (если существуют несколько точек с одинаковыми значениями, то выбирается любая из них с наибольшим (наименьшим) значением).

• 2)    Построение прямой, проходящей через точки L и R , и разбиение множества всех точек на два подмножества: расположенных выше и ниже прямой LR соответственно.

• 3)    Рассмотрение подмножества точек, расположенных выше прямой LR . Выбор точки p 1 , являющейся наиболее удалённой от прямой LR (если для нескольких точек расстояние до прямой LR одинаково, то выбирается та, у которой угол p 1 LR наибольший). Точка p 1 признается вершиной ВО.

• 4)    Построение прямых Lp 1 и p 1 R . Исключение из дальнейшего рассмотрения точек, расположенные справа от прямых, как внутренних точек треугольника p 1 R , не могущих принадлежать ВО.

• 5)    Рассмотрение подмножество точек, расположенных слева от прямой Lp 1 , для которого находится точка p 11 , наиболее удаленная от прямой Lp 1 (аналогично п.3). Точка p 11 признается вершиной ВО.

• 6)    Для всех последующих образующихся подмножеств проводятся операции, аналогичные п.4 и п.5, пока слева не останется ни одного подмножества, созданного ранее.

• 7)    Аналогично пп.3-6 рассматривается подмножество точек, расположенное ниже прямой LR.

Пример, демонстрирующий работу алгоритма Джарвиса, приведен на рис. 4. Вычисли-

В лучшем случае задача разбивается на две равномощные подзадачи, тогда сложность алгоритма определяется рекурсивным уравнением и составляет от 2 q до q ². Достоинством алгоритма Джарвиса является возможность параллельных вычислений для всех подмножеств точек.

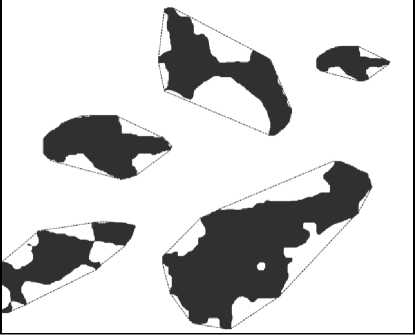
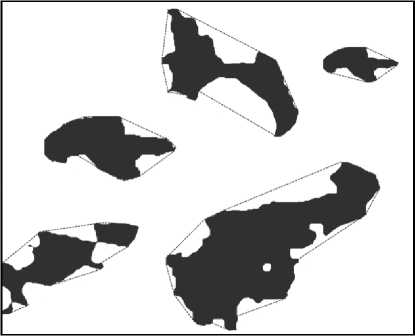
Экспериментальные результаты. Рассмотренные алгоритмы нахождения ВО были исследованы на бинарных изображениях простых фигур (типа звезды) и перлитных пятен. На простых фигурах все алгоритмы показали правильный результат с небольшим различием в быстродействии. На бинарных изображениях реальных объектов – перлитных пятен, полученных из изображений микроструктур металлических трубопроводов, алгоритм Джарвиса и алгоритм БВО выделяют ВО пятна перлита правильно (рис. 5а), в отличие от алгоритма Грэхема (рис. 5б), дающего ошибки выделения ВО. При этом среднее время работы алгоритма Грэхема (≈12 мс) примерно в 1,1 раза меньше, чем у алгоритма БВО и в 1,9 раза меньше, чем у алгоритма Джарвиса (вычисления производились на ПК AMD Athlon II X2 3ГГц с ОЗУ 3Гбайт).

а

б

Рис. 5 . Пример выделения выпуклых оболочек перлитных пятен: а - алгоритмы БВО и Джарвиса, б - алгоритм Грэхема

После нахождения ВО перлитных пятен, необходимо найти их параметры. Исследования показали, что ВО перлитного пятна сильно коррелированна с простой геометрической фигурой - эллипсом, особенно после обработки сглаживающим фильтром, имеющем размер около 10% размера ВО. При этом параметром вытянутости может служить отношение большой и малой полуосей эллипса, а угол вектора направленности соответствует углу направления большей полуоси.

Выбрав изображение эллипса в качестве настраиваемого шаблона S ( a ) ВО S перлитного пятна нужно задать модель подстройки (совмещения) эталона. Например, это может быть модель деформации системы координат, в которой задан эллипс, в частности, содержащая параметры а : угол поворота ф , коэффициенты масштаба k x и k y , параллельный сдвиг ^h = ^{( h} x , h y ) . Тогда координаты точки ( ху ) на изображении шаблона S ( a ) в соответствии с заданным вектором параметров а = ( h_x, h_y , ф , k x , k_y T будут соответствовать координатам точки на изображении ВО:

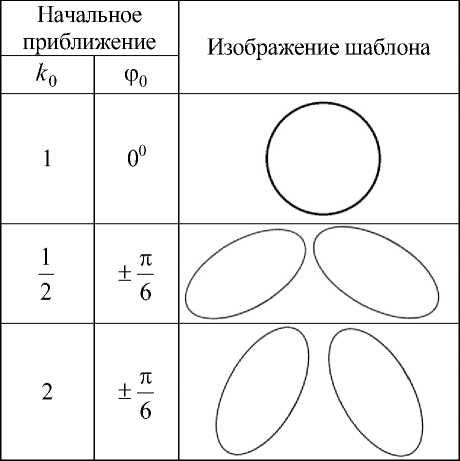
~ = x 0 + kx ((x - x 0 )cos ф - k (y - y 0 )sin ф) + hx, ~ = y о + kx((x - x о)sin Ф + k (y - y о )cos ф) + hy, где коэффициент k=ky/kx является оценкой вытянутости, а ф - оценкой направленности перлитного пятна; (х0,уо) — координаты центра поворота, в качестве которого можно выбрать центр тяжести пятна. Указанные параметры могут быть найдены с помощью адаптивных псевдо-градиентных процедур [4]. Поскольку рабочий диапазон этих процедур ограничен [9], целесообразно задать несколько начальных приближений параметров k и ф (а также kx и h ). Исследования показали, что для параметров k и ф в рассматриваемой задаче, как правило, достаточно пяти начальных приближений шаблона (табл. 1).

Таблица 1 . Пример набора эталонов

Сравнение предложенного подхода с другими возможными способами оценки параметров перлитных пятен из работы [10], показало высокую надёжность предлагаемого подхода.

Выводы: в работе исследованы наиболее популярные алгоритмы выделения выпуклой оболочки: Грэхема, Джарвиса и БВО. Показано, что с небольшим различием в быстродействии все алгоритмы уверенно работают на простых изображениях. На реальных бинарных изображениях зерен перлита, полученных из полутоновых изображений поверхностей металлических структур, алгоритм Грэхема делает ошибки при выделении ВО. Алгоритмы Джарвиса и БВО дают правильный результат, но алгоритм Джарвиса существенно медленнее. Таким образом, для рассмотренной задачи с точки зрения быстродействия и точности наиболее приемлемым является алгоритм БВО.

Работа выполнена при финансовой поддержке гранта РФФИ № 13-01-00555 _а.