Применение анимационных рисунков при обучении школьников-билингвов на уроках алгебры

Вайнштейн Юлия Владимировна - доктор педагогических наук, профессор кафедры прикладной математики и анализа данных, Сибирский федеральный университет (Красноярск); ORCID: ; Scopus Author ID: 57205328429; e-mail:

Постановка проблемы. В соответствии с федеральными государственными образовательными стандартами (ФГОС) для полного среднего образования овладение информационными технологиями выступает неотъемлемым аспектом изучения математики и информатики. В результате изучения базового курса математики учащиеся должны обладать следующими навыками:

• -    уметь применять компьютерные технологии для поиска решений, а также для визуализации уравнений, задач, неравенств;

• -    уметь применять компьютерные программы для вычислений и анализа данных.

Вышеперечисленные требования актуализировали проблему эффективного использования различных цифровых средств, а также компьютерных технологий в процессе обучения алгебре. При этом важным аспектом выступает то, что в образовательной системе Республики Тыва можно наблюдать взаимосвязь проблем при сдаче основного государственного экзамена по математике у школьников с недостаточным уровнем владения русским языком. Педагогические исследования, посвященные проблеме билингвального обучения, показывают, что уровень знания русского языка, на котором ведется обучение, серьезно затрудняет формирование математических базовых знаний у школьников в средних классах [Танзы и др., 2020]. Потенциал компьютерных технологий в процессе обучения алгебре открывает новые возможности для решения этой проблемы.

Это актуализирует цель настоящей работы, которая состоит в создании анимационных рисунков в динамической среде GeoGebra с поддержкой на тувинском языке и применении их в обучении алгебре учащихся-билингвов седьмого класса.

Методология исследования базируется на системно-деятельностном (Л.C. Выготский, А.Г. Асмолов, П.Я. Гальперин и другие исследователи), личностно ориентированном (Ш.А. Амонашвили, Е.Н. Ильина, И.С Якиманская и др.), когнитивно-визуальном (Р. Арн-хейм, Д. Гильберт, В.А. Далингер и др.), исследовательском (Н.Г. Алексеев, Т.А. Иванова, А.В. Леонтович и др.), билингвальном (П.А. Юдакин, У. Ламберт, Я.А. Коменский и др.) подходах к обучению математике.

В качестве теоретических методов исследования применен сравнительно-сопоставительный анализ научно-педагогической литературы. В качестве эмпирических методов использовались экспериментальное обучение алгебре учащихся-билингвов с применением анимационных рисунков, сопровождаемых переводом на тувинский язык, анкетирование для сбора обратной связи от учащихся-билингвов, метод статистической проверки гипотез для оценки результативности педагогического эксперимента – t-критерий Стьюдента.

Обзор научной литературы . При создании методики обучения алгебре с применением компьютерных технологий учитывались возможности среды GeoGebra, раскрываемые в публикациях [Hdez, Perdomo-Díaz, Camacho, 2020; Abboud, 2023; Radović et al., 2020; Safonov, Bakaeva, Tagaeva, 2019]. При этом отметим, что полученные результаты являются продолжением исследований, отраженных в публикациях [Ларин, Чилбак-оол, 2018; 2019; 2020; Сарыглар, 2021а, б; 2022; Ларин, Сарыглар, 2022], и представляют инновационное методическое обеспечение для утвержденных учебников по алгебре седьмого класса [Макарычев и др., 2023; Мерзляк и др., 2015]. Проблемы и перспективы би-лингвального обучения в Республике Тыва рассматриваются в исследованиях [Танзы и др., 2020; Taryma, 2019]. Теоретические и практические аспекты развития математического образования в условиях цифровизации опубликованы в научных статьях [Shabanova, Udovenko, Nimatuliev, 2019; Vainshtein et al., 2019; 2020; Hai, Van, Thi Tuyet, 2021; Zehavit et al., 2022].

Для формирования у учащихся понятия «компьютерно-математическая модель» на уроках алгебры в работе применена широко распространенная динамическая среда GeoGebra [Abebayehu, Hsiu-Ling, 2023]. Она является одним из инструментов в арсенале цифрового образования [Майер, Семина, 2014]. Данная программа активно используется для создания анимационного контента на уроках алгебры. Предоставляя три вида анимации – геометрическую, алгебраическую и текстовую, – среда служит мощным инструментом для решения и моделирования разнообразных математических задач [Абдулкин и др., 2019]. Это позволяет учащимся преодолеть проблемы, связанные с длительными вычислениями, и сфокусироваться на понимании алгоритмов и концепций.

Результаты исследования. Рассмотрим методику построения урока с применением анимационных рисунков по теме «Умножение иделение степеней». На уроке учителем о время закрепления теоретического материалы предлагается учащимся решить в тетрадях упражнения 403, 404, 414, 415, 438 из учебника [Макарычев и др., 2023], а затем, используя анимационный рисунок и устанавливая с помощью ползунков значения параметров a, m, n, проверить полученные ответы. Далее учащимся предлагается проговорить правила умножения и деления степеней с одинаковыми основаниями и возведения степени в степень. При рассмотрении таких вопросов, как «Умножение и деление степеней», «Возведение в степень произведения и степени», можно наглядно продемонстрировать с применением анимационного рисунка «Действия над степенями» (чадалар-биле кылдыныглар): умножение степеней, деление степеней и возведение степени в степень (рис. 1). При использовании данного рисунка при наличии языковых сложностей можно применять билингвальную поддержку, включив «Перевод на тувинский язык / тыва дылче очулгазы».

= GeoGebra

Дейсвия над степенями

Я Перевод на тувинский язык/тыва дылга очулгазы

ДЕЙСТВИЯ НАД СТЕПЕНЯМИ

ЧАДАЛАР-БИЛЕ КЫЛДЫНЫГЛАР

Введите число а

а = -10

а дел санны полэунокка базынар

Установите показатель m

m = 6

m биле п-нин кергузуун

Установите показатель п

п = 4

ползунокка тургузуцар

а"1- а" = а’

-106. -104 = -1010 = 10000000000

а : а = а

-106 : -104 = -102 = 100

= a

(-ю6)4 = — 10м

Ажтивйцие Window*

::

Рис. 1. Анимационный рисунок «Действия над степенями»

Fig. 1. Animation drawing “Actions with degrees”

При изучении темы «Умножение одночленов. Возведение одночлена в степень» можно применять анимационный рисунок «Действия над одночленами ( чаӊгыс кежигүннүг кергуз/г-биле кылдыныглар ) (рис. 2). Он наглядно демонстрирует умножение одночленов и возведение одночлена в степень, что позволяет учителю при объяснении темы с помощью ползунков моделировать и визуализировать решения примеров из учебника [Макарычев и др., 2023].

Рассмотрим пример по теме «Формулы сокращенного умножения». Данную тему предлагается сопровождать анимационным рисунком для ускорения запоминания и проверки

знания формул сокращенного умножения (рис. 3), то есть эффективно использовать его в качестве тренировочно-тестирующего задания, когда нужную формулу можно с помощью флажка открыть/скрыть, а также показать перевод на тувинский язык согласно персональному запросу учащихся.

Также данную тему целесообразно дополнить анимационной моделью квадрата суммы, являющегося одной из основных формул. Анимационный рисунок «Анимационная модель квадрата суммы» (см. упражнение 861 [Макарычев и др., 2023, с. 142]) позволяет перемещать точки A и B , при этом визуализируя изменение длин отрезков a , b (рис. 4).

= GeoGebra                                                                                                                   назначать | ■ действия над одночленами

ДЕЙСТВИЯ над одночленами

Установите коэффициенты к и к1

Установите показатели степеней т, п, р, q и т^ n1t pr qr

А = kambncpdql В = kiamibnidP1dqi D Перевод на тувинский язык/ тыва дылче очулгазы о Чангыс кежигугуннуг кергузуг-биле кылдыныглар к биле дел коэффициентилерни тургузунар к = 9.1 к- =-6.1                            1

--•—  —»-- m = 3 n = 8       4 q = 2 m,n,p,q болгаш m1,n1,p1lq1 деп чадаларнын

•----- •      •----- •----- кергузуглерин тургузунар т1 = 1 п1 =4 Р1 = 2 Qf = 2

Установите степень г, в которую нужно воз^сти одночлен А е е А деп чангыс кежигугуннуг кергузугну г - 5 г деп чадаже кедурерде,

А- В = 9.13b⁸c⁴d²- -6.1aWd² = -55.514b¹²e⁶d⁴;

А^т = (9.1«Wd²)⁵ = Э.!⁵»³'⁵^⁴^⁵'² = 62403.21a¹⁵b⁴W°.

Активация Windows

Чтобы активировать Windows, перейдите в раздел "Параметры

Рис. 2. Анимационный рисунок «Действия над одночленами»

Fig. 2. Animation drawing “Actions with monomials”

= GeoGebra

НАЗНАЧАТЬ •

Формулы сокращенного умножения

Автор: Сайдыс

В Перевод на тувинский язык/тыва дылче очулгазы

ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ Кевуделгениц хураангайлаан формулалары

8 Формула квадрата суммы (а + б)2 = а? + 2аб + b’ 8 Формула квадрата разности (а - б)3 = a2 - lab + b2 8 Формула куба суммы (а + 6)3 = а3 + ЗаЧ + 3ab2 + i3 8 Формула куба разности (а - Ь)3 = а3 - За26 + Заб2 - б3 8 Формула разности квадратов а2 - б2 = (а - 6) (а + б) 8 Формула суммы кубов а3 + б3 = (а + б)(а2 - аб + б2) В Формула разности кубов a3 - б3 = (а - 6)(а2 4- аб^

Кевудел гениц хураангайлаан формулаларын ееренип алгаш, бопарынарны хынаарда кек ецнуг тукчугашче базыптыцар. Ол формулаларже кэргеш, шын номчуп, адап ееренинер.

Рис. 3. Анимационный рисунок «Формулы сокращенного умножения»

Fig. 3. Animated drawing “Abridged multiplication formulas”

= GeoGebra

КВАДРАТ СУММЫ

Длины отрезков а и b регулируются перемещениями

В качестве анимационной поддержки темы «Решение систем двух линейных уравнений с двумя неизвестными» наиболее эффективным средством выступают анимационные рисунки тренинго-тестирующего характера с использованием возможностей открыть/скрыть решение и ответ. При этом используются средства анимации «флажок», «ползунок» и «условия видимости». Таким образом, появляется возможность тиражировать однотипные задания разной сложности, например задания по решению систем линейных уравнений с двумя переменными методом подстановки (рис. 5) при значении ползунка n = 1.

методом подстановки

Перемещайте

Установите коэффициенты и свободные члены п=1 турда, ползуноктарнын коэффициентилерин шилип алыры, п ийиден сеске чедир белук деннелгелерни орнунга салып тургаш бодаар арга-биле бодаары, п=9 турда, харыызын кееру

а = 2 Ь = -3

с = 5

а^4 Ь.

-3

Рис. 5. Анимационный рисунок «Решение СЛУ с двумя переменными методом подстановки» (создание системы)

Fig. 5. Animated drawing “Solving a case with two variables by substitution method” (creating a system)

При перемещении значения ползунка от стрируется пошаговое решение СЛУ с двумя пе- n=2 до n=8 на анимационном рисунке демон- ременными методом подстановки (рис. 6).

Рис. 6. Демонстрация пошагового решения задачи

Fig. 6. Demonstration of a step-by-step solution to the problem

И наконец, на анимационном рисунке (рис. 7) при пермещении ползунка n = 9 появляется ответ решения СЛУ с двумя переменными методом подстановки.

На уроках алгебры в седьмом классе в условиях двуязычия учителю предлагается использовать готовые динамические анимационные рисунки в среде GeoGebra, где можно менять значение ползунка с помощью перемещения точки, а также использовать флажок при включении или выключении анимации и билингвальной поддержки. В качестве учебно-

Рис. 7. Демонстрация ответа на задачу

Fig. 7. Demonstration of the answer to the problem

исследовательских задач можно рассматривать задачу на равномерное прямолинейное движение, например катера по реке или озеру, на базе использования анимационного моделирования, что вызывают большой интерес у учащихся.

Педагогический эксперимент был проведен на базе МБОУ «Гимназия № 5» города Кызыла Республики Тыва. В эксперименте приняли участие обучающиеся 7 классов в количестве 50 человек, из них 25 человек – контрольная группа и 25 – экспериментальная.

Для школьников экспериментальной группы было проведено анкетирование по теме «Умножение многочленов» с применением анимационных рисунков на уроке алгебры седьмого класса. Анкетирование показало положительную реакцию на внедрение анимационных рисунков с билингвальными подсказками при изучении тем алгебры седьмого класса. Например, при анкетировании 88 % школьников подтвердили повышение интереса к изучению предмета с анимационным контентом, ответив на вопрос «Повышает ли интерес к изучению алгебры применение на уроке анимационных рисунков c билингавльной поддержкой?», 4 % пояснили, что можно проводить урок традиционным способом, и 8 % затруднились ответить на вопрос (рис. 8).

100%

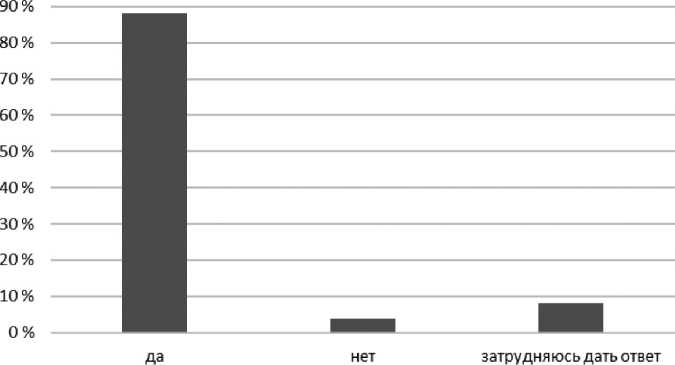
Рис. 8. Оценка влияния анимационных рисунков на повышение интереса к изучению алгебры

Fig. 8. Assessment of the influence of animated drawings on increasing interest in the study of algebra

При оценке удобства применения билинг- в 10 баллов, 24 % поставили 9 баллов, 12 % – вальных подсказок 64 % учащихся оценили ее 8 баллов по 10-балльной шкале (рис. 9).

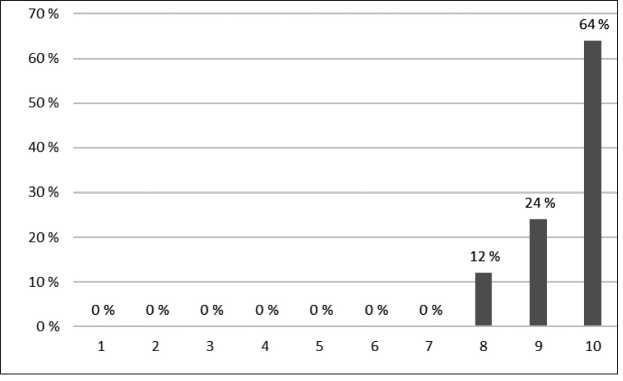
Рис. 9. Оценка удобства применения билингвальных подсказок

Fig. 9. Evaluating the usability of bilingual prompts

При оценке влияния анимационных рисунков на понимание предмета согласно мнению самих учащихся: 92 % отметили повышение понимания алгебры, 4 % затруднились дать ответ и лишь для 4 % предложенный под-

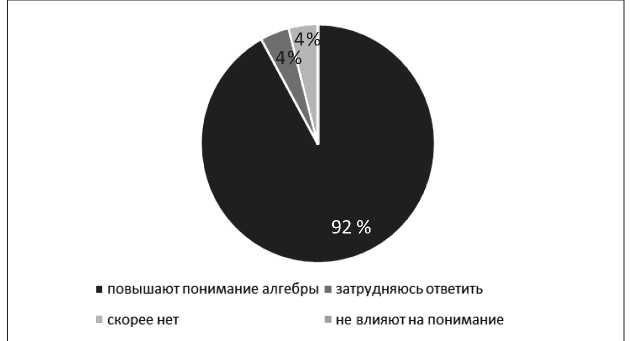
Рис. 10. Оценка влияния анимационных рисунков на мотивацию

Fig. 10. Assessment of the influence of animated drawings on motivation

Для проверки знаний были проведены входной и итоговый контроль для учащихся экспериментальной (ЭГ) и контрольной (КГ) групп по темам: «Сложение и вычитание многочленов», «Умножение одночлена на многочлен. Умножение многочлена на многочлен» и «Разложение многочлена на множители» – и сравнение результатов контроля с применением t-критерия Стьюдента. Гипотеза H0 заключалась в отсутствии различий между ЭГ и КГ ход показался скорее не влияющим на понимание, за полное отсутствие повышения понимания алгебры, изучаемой с применением анимационных рисунков, не высказался никто (рис. 10).

независимо от применяемого в обучении алгебре подхода. Гипотеза H₁ состояла в том, что учащиеся-билингвы ЭГ имеют более высокие образовательные результаты, то есть различия между группами статистически значимы. Во время входного контроля по всем темам получено, что статистически значимых различий в ЭГ и КГ нет. Во время итогового контроля подтверждено, что ЭГ и КГ значимо отличаются между собой (табл.).

Результаты применения t -критерия Стьюдента Results of applying Student’s t-test

Показатель	Входной контроль		Итоговый контроль
t кр	2,01
Уровень значимости α	0,05
Тема «Сложение и вычитание многочленов»
t эмп	1,3	3,5
Вывод	H 0 принимается	H 0 отклоняется
Интерпретация	Статистически значимых различий между ЭГ и КГ нет ( t 3„n <  t w)	ЭГ и КГ статистически значимо различаются ( t эмп < t kp )
Тема «Умножение одночлена на многочлен. Умножение многочлена на многочлен»
t эмп	2	2,8
Вывод	H 0 принимается	H 0 отклоняется
Интерпретация	Статистически значимых различий между ЭГ и КГ нет ( t эмп < t kp )	ЭГ и КГ статистически значимо различаются ( t эмп < t kp )
Тема «Разложение многочлена на множители»
t эмп	1,3	2,7
Вывод	H 0 принимается	H 0 отклоняется
Интерпретация	Статистически значимых различий между ЭГ и КГ нет ( t эмп < t „p )	ЭГ и КГ статистически значимо различаются ( t эмп < t kp )

Заключение. Обучение алгебре в седьмом классе с применением анимационных рисунков, сопровождаемых поддержкой на тувинском языке, положительно воспринимается тувинскими школьниками, повышает понимание предмета и интерес к его изучению с помощью наглядности.

Анимационные рисунки, созданные в динамической среде, расширяют арсенал средств обучения математике в условиях двуязычия. Они вы- ступают для школьников средством экспериментирования, поиска решения задач, реализации математических алгоритмов с устранением вычислительных трудностей и демонстрации анимационных моделей изучаемых формул, процессов и явлений природы. Самостоятельное созда- ние школьниками анимационных рисунков под руководством учителя может стать основой проектной деятельности с дальнейшим представлением ее результатов на школьных конференциях.