Применение биоинспирированных методов при моделировании токсических характеристик поршневых двигателей внутреннего сгорания

Введение. При изучении внутрицилиндровых процессов в поршневом двигателе внутреннего сгорания (ДВС) методами нелинейной динамики две практически важные задачи проблематично решить регулярными численными методами [1]. Первая состоит в отыскании стационарных и/или равновесных состояний, вторая – в быстром прогнозировании отклика эволюционирующей физико-химической системы на управляющие воздействия. Источник трудностей – высокая размерность и многомасштабность рабочего процесса ДВС как динамической системы. Определенные надежды в предметных исследованиях возлагаются на генетические алгоритмы и нейросети [2].

Применительно к компьютерной имитации рабочего процесса в ДВС авторами разработаны оригинальные вычислительные методы:

– генетический алгоритм отыскания равновесного и/или стационарного состояния физикохимической системы с реакциями и фазовыми переходами;

– процедура оценивания решения задачи Коши применительно к впрыску, смесеобразованию, горению и образованию токсичных веществ в условиях ДВС.

Постановка задачи. Определение равновесного состава некоторой фиксированной массы реагирующей, например, однофазной среды при заданных температуре и давлении, осуществляется путем минимизации суммарного термохимического потенциала системы [3]

G = ^ m j ■ j Ц j

g j + RT ln( M ■ P ) + In

V

( m )

V ^ц j 7

^ min

при материальных ограничениях am - ma = 0 . (2) В (1), (2) a - массовая доля атомов /-го сорта в веществе j, a = {ai,j}; m - вектор масс веществ, m = {mj}; ma - вектор масс атомов сорта, ma = {mai}; цj и gj - молярная масса j-го вещества и его химический потенциал соответственно; M и P – общие масса и давление соответственно; gj (T) = H + Cpj (T - 298) - T (Sj + Cpj InT / 298), где Hj, Cpj, Sj - энтальпия образования, теплоемкость при постоянном давлении и энтропия j-го вещества при температуре T = 298 K соответственно.

*

Работа выполнена при поддержке Фонда ALCOA.

Минимизированию (1), (2) посредством известных генетических алгоритмов [1] препятствуют жесткие ограничения (2): обычно вместо условного минимума (1), (2) ищут абсолютный минимум модифицированного функционала

m

G = У -1j ^ j

g j + RT ln( MP ) + In

I

^ (■ ]]

+ X ( a m - m a )² ^ min .

Метод решения. Классические генетические алгоритмы применяют для задач минимизации на компакте параметров:

F(x) > min(4)

a, > xi > bi, i = 1,2...N .(5)

Если в задаче имеются еще ограничения типа

g(x) < 0 - покомпонентно,(6)

их модифицируют следующим образом:

g(x,g) = g(x) + 5 = 0, 5j > 0, j = 1,2...M .(7)

Задача сводится к

F (x,5,X) = F(x) + ^Xj ■ 11gj(x, aj)|| ^ min(8)

j = 1

с ограничением (5), где X j >  0, j = 1,2... M подбирается исследователем из расчета

Xj ~ и, ^x)" и. Норму здесь берут евклидову ||gj (x, 5)|| = (gj (x, 5))2, а для подбора X исполь-gj(x,5 j )|| зуют норму Чебышева, т. е. Xj ~

max, (| F ( )< )|)

ai >  x-i >  bi ^{Vl          17}

max (д,.(.х , 5 ai >  xi >  biV³)⁴

При высокой размерности i , j задачи вероятность выхода популяции на ограничения (1) ничтожна, и процесс поиска приходится обрывать в одном из локальных минимумов. Понижение размерности системы путем исключения компонентов на основании (1) приводит к артефактам типа отрицательных концентраций или масс.

Принципиальная новизна предлагаемого подхода состоит в переносе ограничений (2) из адаптивной функции в кодировку хромосома: в классическом алгоритме кодировка гена ограничена фиксированным интервалом [ a , b ], а в модифицированном этот интервал приобретает определенную подвижность в соответствии с ограничениями (2). При каждой генерации гена ищутся граничные значения a и b с учетом реализации предыдущего гена и ограничений (2). Физические соображения позволяют заметно сузить интервал локализации экстремума как сверху (ресурсом свободных атомов), так и снизу (устранением невязки материального баланса). Фактически алгоритм позволяет выбрать базовые компоненты. Резюмируя, грубые локализующие свойства ограничений (2) выносятся в алгоритм, а тонкие уточняющие сохраняются в самих уравнениях.

Если в классическом алгоритме кодировка гена ограничена фиксированным интервалом [ a , b ] , то в модифицированном этот интервал приобретает определенную подвижность в соответствии с ограничениями (5), (6). При каждой генерации гена ищутся граничные значения a и b с учетом реализации предыдущего гена и действующих ограничений, т. е. для каждого i -го гена i = 1... N - 1 ищется максимум при линейных ограничениях (10) и условии (11):

m i ^ max

при линейных ограничениях i-1

«1 imi + «12mi+1 + ... + aiNmN = mai - ^«1 mj j=1

i - 1

« 2 i m i +“ 22 m i . 1 ⁺ ■•• + “ 2 N m N = m .2 - 2 a j m j

'

...

i - 1

^a Mi m i ^{+ a} Mi m i + 1 ⁺ ... ^{+ a} MN m N = m aM ^- 2 ^a Mj m j j = 1

N +1 - i и условиях mi > mmn i , i = I-2" N .

В результате находится верхний предел значения m_i , т. е. соответствующее значение b . Генерация гена происходит также случайно, но уже с вновь вычисленным значением b , т. е. m i e [ a , b ( m_k ) ] , где k = 1... i - 1. Соответственно первый элемент зависит только от ограничений (2). Решая на каждом шаге систему (9) – (11), например симплекс-методом, находим вектор m . Так формулируется универсальная методика нахождения минимума функционала с линейными ограничениями при помощи генетического алгоритма. Важно отметить, что система уравнений имеет высокую размерность только для первых m .

Предложенная здесь модификация гарантирует выполнение различных сложных ограничений. При использовании в алгоритме гена большой длины (обычно применяют кодирование минимальной длиной 2 байта) и умеренного числа элементов этот алгоритм быстрее классического. Максимальное число итераций для классического алгоритма P _кл и модифицированного P _м можно рассчитать по формулам

Р- = 2 L M ,                                             (12)

Р м = N 2 M ,                                        (13)

где L – длина гена, M – число ограничений, N – число элементов в системе. Из формул (12), (13) следует, что модифицированный алгоритм эффективен при N <  2 L/2 . При хорошей точности N <  2^16/2 = 256, а при высокой - N <  2^32/2 = 65536 .

Усовершенствованный алгоритм в сочетании со стандартным симплекс-методом решения (9)–(11) требует объемных вычислений при каждой генерации гена и таким образом оказывается неэффективным при решении задачи (1), (2). Поэтому здесь можно воспользоваться свойством системы aij > 0 и не решать (9)-(11), а просто ограничить следующий генерируемый ген остатка- ми масс элементов:

(           i - 1           ^

mak -2akjmj bi

= min ------ j -¹------

Н¹- M J          a _ki

V 7

Фактически предлагаемый способ реализует выбор самим генетическим алгоритмом базовых компонентов в реагирующей системе, однако при этом не гарантируется строгое соблюдение материального баланса. Это несовершенство метода легко устраняется классической коррекцией, состоящей в замене минимизации (1), (2) на минимизацию (3). Таким способом локализующие масштабные свойства ограничений (2) вынесены в алгоритм, а тонкие уточняющие – в уравнения. В основу предложенного разделения масштабов положены естественные физические соображе- ния: они позволяют заметно сузить интервал локализации экстремума как сверху – ресурсом свободных атомов, так и снизу – устранением невязки материального баланса.

При введении в систему свободных химических элементов (что не противоречит физическим законам, но в некоторых случаях нежелательно ввиду их низкой концентрации) ограничение по минимальному остатку элемента удовлетворяет условиям (2) всегда: остаток элемента выступает как компонент системы. Такой подход является более общим при рассмотрении систем с большим числом элементов, компонентов и реакций.

Реализация и результаты вычислительного эксперимента. Интерфейс компьютерной реализации алгоритма показан на рис. 1. Термохимические константы реагентов, продуктов и промежуточных веществ хранятся в проблемно-ориентированной БД. На данный момент также реализованы функции импорта первичной термодинамической информации из стандарта программы STANJAN [4].

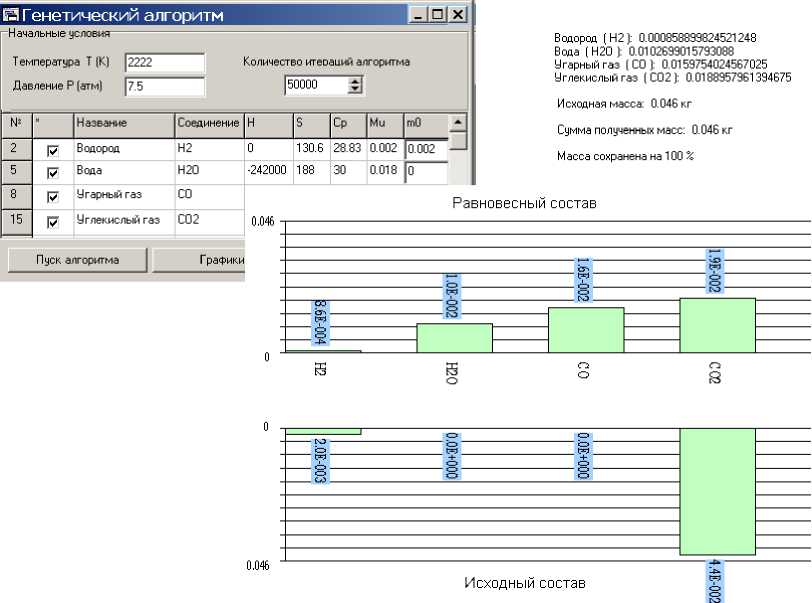
Рис. 1. Результат расчета равновесного состава в системе CO 2 (1 моль) + H 2 (1 моль) ↔ CO + H 2 O при Т = 2222 К, P = 7,5 атм

Верификация алгоритма осуществлялась на интересных для авторов системах: крекинг углеводородов, горение традиционных нефтегазовых и перспективных спиртовых моторных топлив, продукты сгорания различных ракетных топлив. Пример такого сопоставительного расчета приведен на рис. 2: посредством усовершенствованного генетического алгоритма определен равновесный состав системы H 2 O – H 2 – OH – O 2 – O – H при давлении 5 атм в диапазоне температур 2000–6000 К. Результаты сопоставления рассчитанного равновесного состава продуктов сгорания различных моторных и ракетных топлив с данными работ [5], [6] свидетельствуют, что главные компоненты химического равновесия определяются предложенным методом вполне надежно.

Во всех изученных системах содержание основных компонентов определялось при помощи усовершенствованного генетического алгоритма с приемлемой погрешностью. Зная содержание всех ведущих компонентов, нетрудно рассчитать также важные, например, в плане токсичности, малые составляющие равновесной смеси. Это ценно, поскольку размерность задачи существенно

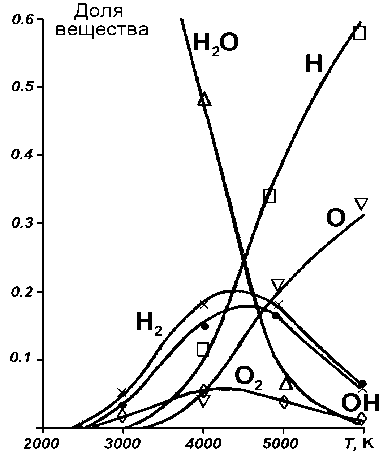
Рис. 2. Рассчитанные парциальные концентрации компонентов:

A - H 2 O, x - H 2 , • - OH, ◊ - O 2 , □ - H, V - O (сплошные линии -эталонные данные [6])

зависит от того, насколько верно удается априорно выбрать номенклатуру главных компонентов в химическом равновесии.

Перспективы развития биоинспирированных методов. Отрабатываемый авторами нейросетевой алгоритм быстрого оценивания решения задачи Коши сейчас «обучается» на фраг-ментных задачах:

– имитация динамики распыла – испарения в условиях дизеля;

– прогнозирование мощности и экономичности рабочего цикла по входным параметрам;

– определение содержания токсичных веществ в отработавших газах.

Следует отметить, что если «обучение» возможностям первой и второй задачи удается ограничить расчетными «обучающими» данными, для уверенного прогнозирования токсичности выхлопа приходится привлекать экспериментальный материал. Тем не менее, об адекватности этого алгоритма целям со- вершенствования программного комплекса «Мотор» [7], [8] свидетельствует успешность «обучения» нейросети на результатах представительного множества численных расчетов. Сеть позволяет прогнозировать токсичность выхлопа известного ей двигателя в пределах обучающей выборки. Однако в силу существенной нелинейности внутрицилиндровой физико-химической кинетики на- дежность такого прогнозирования пока недостаточна.

Внедрение новых биоинспирированных имитационно-аналитических средств в состав системы «Мотор», интерфейс и некоторые возможности которой показаны на рис. 3, расширяет ее функциональность, прежде всего, в части приспособленности для комплексной оптимизации и управления внутрицилиндровыми процессами.

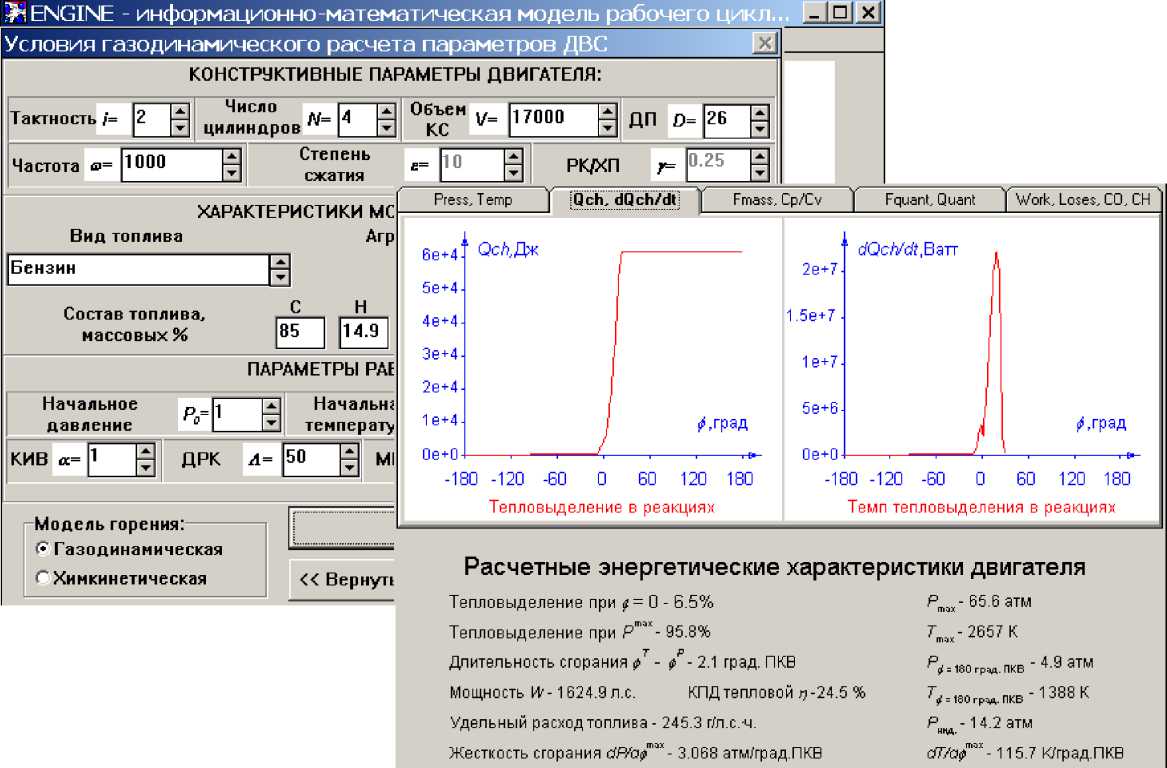
Рис. 3. Интерфейс и функциональность программного комплекса «Мотор» [8]

Заключение. Предложено усовершенствование генетического алгоритма для расчета стационарных состояний динамических систем химической природы, например, двигателя внутреннего сгорания. Особенностью разработки является разнесение малых и больших параметров уравнений между уравнениями и алгоритмом их решения.

На данный момент интегрированная в комплекс «Мотор» [7], [8] система моделей и методов, в том числе биоинспирированных, позволяет:

• –    рассчитывать энергетические характеристики ДВС и токсичность выхлопа по СО, C x H y , RCHO, NO при использовании различных топлив и на переходных режимах;

• –    выявлять ведущие физико-химические процессы во внутрицилиндровой кинетике;

• –    анализировать динамику внутрицилиндровых процессов и вырабатывать способы их оптимизации;

• –    формулировать критерии параметрической оптимизации;

• –    разрабатывать эффективные способы управления.