Применение численного метода для расчета корректировок цен объектов-аналогов в рамках сравнительного подхода

В статье 22 Федерального стандарта «Оценка недвижимости (ФСО № 7)», утвержденного приказом Министерства экономического развития Российской Федерации в 2014 году, отмечается, что в зависимости от имеющейся на рынке исходной информации в процессе оценки недвижимости могут использоваться качественные методы оценки (относительный сравнительный анализ, метод экспертных оценок и другие методы), количественные методы оценки (метод регрессионного анализа, метод количественных корректировок и другие методы), а также их сочетания.

В рамках сравнительного подхода к оценке стоимости недвижимости среди количественных методов оценки с давних времен наиболее популярным является метод корректировок цен аналогов объекта оценки (далее – аналог) (см. [2, 3]), который, по сути, отражает размышления продавцов и покупателей при определении цены сделки. Суть метода корректировок состоит в подборе некоторого количества аналогов (обычно 5–10) с известными ценами сделок и (или) предложений, анализе отличий их ценообразующих характеристик от характеристик объекта оценки, корректировке цен каждого из выбранных аналогов посредством «устранения» выявленных отличий и расчете стоимости объекта оценки на основе информации о скорректированных ценах аналогов. То есть в отличие от метода регрессии этот метод, применяемый для массовой (кадастровой) оценки (подробнее см. [4]), можно использовать на рынках, не изобилующих рыночной информацией. Применение этого метода усложняется следующими проблемами:

• 1)    корректный подбор сопоставимых с объектом оценки аналогов;

• 2)    определение объективных корректировок или поправок цен этих аналогов.

Проблема подбора сопоставимых с объектом оценки аналогов, от которых зависит итоговый результат оценки, решается посредством анализа различных баз данных, информации из интернета, средств массовой информации в регионе оценки и изучения полученной информации об аналогах на предмет сопоставимости их с объектом оценки по принципу «чем ближе характеристики аналога к характеристикам объекта оценки, тем меньше величина корректировки цены аналога и тем точнее оценка объекта оценки» и изучения цен этих аналогов на предмет достоверности. Важным моментом здесь является изучение структуры цены каждого аналога для учета этой структуры в процессе корректировки цены аналога. Корректность выбора аналогов можно также проверить посредством анализа коэффициентов корреляции цен аналогов с ценообразующими факторами. Знаки и значения коэффициентов корреляции не должны противоречить рыночным тенденциям.

Для расчета же корректировок или поправок выбранных цен аналогов часто используют метод «парных продаж» (см. [3, 5]), когда сравнивается пара объектов-аналогов одинаковых или близких по своим ценообразующим характеристикам, кроме одной характеристики, и вычисляется разница их цен, отнесенная на разницу в значениях этой характеристики. Полученное линейное соотношение далее используется для корректировки цен остальных аналогов. Проблема в том, что достаточно сложно найти на рынке два объекта, отличающиеся значениями только одного ценообразующего фактора. И, кроме того, при использовании этого метода часто одна и та же корректировка может применяться к разным по характеристикам аналогам, что в общем случае неправильно. Так, например, цены помещений аналогов разной площади могут по-разному реагировать на изменение расстояния от центра города или до метро, и, следовательно, корректировки их цен на расстояние в стоимостном выражении должны быть разными. Близким по сути к методу парных продаж является метод матричной или линейной алгебры (подробнее см. [6]). Для него нет необходимости в подборе аналогов, отличающихся только одним фактором, но недостаток этого метода в том, что он основан на решении линейных систем уравнений. Это сужает область его применения, так как зависимость стоимости от факторов часто бывает нелинейной.

Расчет корректировок можно сделать и на основе анализа тенденций ценообразования на рынке объекта оценки, однако это не всегда удается, особенно если рынок нестабилен и цены «скачут». В связи с этим при расчете корректировок оценщики часто обращаются к своим коллегам, мнения которых могут быть субъективными, что снижает доверие к результатам оценки объектов недвижимости с использованием сравнительного подхода. Практика оспаривания кадастровой стоимости показывает, что подавляющее количество замечаний к отчетам об оценке рыночной стоимости относится к выбору аналогов и к результатам корректировки их цен при применении сравнительного подхода. Как отмечено в работе [7], к сожалению, в большинстве случаев оценщики недвижимости делают субъективные, анекдотические, произвольные и ненаучные «корректировки» к данным сопоставимых рыночных сделок без объективного рыночного обоснования.

В статье рассмотрен один из возможных подходов к решению проблемы расчета корректировок при определении рыночной стоимости 1 объекта недвижимости в рамках сравнительного подхода за счет минимизации влияния человеческого фактора на процесс расчета значений этих корректировок (поправок) цен аналогов. Подход основан на действии закона единой цены (the law of one price) на рынке объекта оценки, согласно которому, если на конкурентном рынке проводятся операции с равноценными (эквивалентными, идентичными по своей сути) активами, то их рыночные цены в один и тот же период времени либо будут равны, либо будут стремиться к сближению 2. Закон единой цены предполагает равенство или близкое к равенству цен товаров при условии корректного учета всех издержек, обстоятельств продажи и ограничений (транспортных, правовых, налоговых, финансовых и т. д.), приведших к формированию цены. Этот закон является одним из фундаментальных принципов оценки стоимости активов, используемый в финансовой сфере и оценочной деятельности 3. Если рассматриваемые цены не подчиняются действию этого закона, то первым подозрением станет не догадка о нарушении действия закона единой цены, а предположение о том, что (1) нарушен процесс нормального функционирования конкурентного рынка или (2) между активами существует некое, возможно не установленное аналитиком, отличие. В этом случае любой метод оценки, включая регрессию, будет работать плохо или вовсе не работать.

В рамках настоящего исследования считается, что цены на рынке недвижимости подчиняются закону единой цены, и рассмотрим возможные варианты решения задач оценки объектов недвижимости с использованием метода корректировок сравнительного подхода, основанного на этом законе.

Прежде чем сформулировать общую задачу оценки, приведем несколько, на мой взгляд, важных определений (подробнее см. [5]).

Объекты недвижимости, принадлежащие к одному и тому же сегменту рынка, назовем однородными объектами. При этом сегмент рынка объектов определим как часть рынка объектов недвижимости, имеющих одинаковый набор основных ценообразующих факторов и единообразное ценообразование по каждому из факторов. Иными словами, для всех объектов, принадлежащих одному сегменту рынка, характерна схожесть основных ценообразующих факторов, а ценообразование по каждому отдельному фактору подчиняется единой закономерности и может быть описано одной моделью.

Однородные объекты недвижимости, имеющие одинаковый набор, но разные значения факторов стоимости, назовем гетерогенными объектами , а объекты недвижимости, имеющие одинаковый набор и одинаковые значения ценообразующих факторов – гомогенными объектами . При этом под ценообразующими факторами будем понимать не все характеристики объекта оценки и характеристики его окружения, а только те, которые действительно и значимо влияют на цену.

Переопределенной системой уравнений корректировок назовем систему, количество уравнений которой превышает количество неизвестных параметров, определенной системой уравнений корректировок – систему, количество уравнений которой равно количество неизвестных параметров, неопределенной системой уравнений корректировок – систему, количество уравнений которой меньше количества неизвестных параметров.

Оценка стоимости объекта оценки – процесс оценки стоимости объекта оценки.

Показатель стоимости объекта оценки – результат оценки стоимости объекта оценки.

Факторы стоимости (ценообразующие факторы) объекта оценки – характеристики объекта оценки, от которых зависит стоимость объекта оценки.

Постановка задачи

Последовательность, в которой применяются поправки к сопоставимым объектам, определяется рынком оцениваемого объекта (см. [5]). Наиболее часто поправки по первой группе элементов сравнения или, что то же самое, факторам стоимости (на передаваемые имущественные права, условия оплаты, условия продажи, на расходы в процессе покупки, на рыночные условия), которые, как правило, делаются на стоимостной основе, выполняются таким образом, что каждый раз корректируется откорректированная на предыдущем этапе цена, а поправки же по второй группе факторов (местоположение, физические характеристики, экономические характеристики, вид использования, компоненты, не входящие в состав недвижимости), зависящие от характеристик объекта оценки, выполняются так, что для корректировки цены, полученной после последней корректировки цен по первой группе, предварительно рассчитывается сумма процентных поправок по элементам сравнения из второй группы. В связи с этим уравнения корректировок цен аналогов включают как аддитивные, так и мультипликативные составляющие и, как следствие, пред- ставляют собой систему гибридных 4 нелинейных алгебраических уравнений. Бывает, что базовый элемент сравнения или фактор стоимости разбивают на промежуточные элементы зависимого или независимого типа (подфакторы), которые вносят дополнительные корректировки к базовому элементу сравнения. Например, физические характеристики могут быть разделены на возраст, состояние здания, его размеры и т. п. Все это делает систему алгебраических уравнений еще более сложной для решения. Решение таких задач возможно только приближенными методами.

Математическую модель или систему уравнений корректировок, которую достаточно часто используют в рамках метода сравнительного анализа в индивидуальной оценке недвижимости, на теоретическом уровне можно представить в виде следующей гибридной системы уравнений [5]:

r                   ⎛k⎞

VO=P1×∏(1+aiΔxi1)×⎜1+∑aiΔxi1⎟+ε1 i=1                       ⎝     i=r+1

r                    ⎛k⎞

VO=P2×∏(1+aiΔxi2)×⎜1+∑aiΔxi2⎟+ε2 i=1                          ⎝      i=r+1

⎪                  r                       ⎛k⎞

⎪VO=Pn×∏(1+aiΔxin)×⎜1+∑aiΔxin⎟+εn ⎩                  i=1                       ⎝     i=r+1

где V_O - рыночная стоимость объекта оценки;

Р ₁, Р ₂, …, Р_n – цены аналогов;

a_i ( i = 1, …, k ) - корректирующие (поправочные) коэффициенты или коэффициенты коррекции цен аналогов, измеряемые в долях единицы или в процентах;

Δ x_ij = ( x_ij – x_{i 0}) – разность значений i -го ценообразующего фактора объекта оценки и его j -го аналога;

a_i Δ x_ij – относительная (процентная) поправка к цене j -го аналога по i -му фактору;

k – общее количество ценообразующих факторов (элементов сравнения);

r - количество элементов сравнения в первой группе, характеризующей параметры возможной сделки с объектом оценки;

( k – r ) - количество элементов сравнения во второй группе, которые характеризуют местоположение, физические и экономические ценообразующие характеристики объекта оценки;

ε _j - ошибки корректировок.

В системе уравнений (1) известными величинами являются цены аналогов и значения ценообразующих факторов объекта оценки и его аналогов, неизвестными - искомая стоимость VО и коэффициенты коррекции ai (i = 1, …, k). Система (1) позволяет посредством корректировки цен аналогов решить задачу расчета рыночной стоимости VО объекта оценки. При этом произведение ∏(1 +aiΔxij) представляет собой результат процентной корректировки цены j-го аналога по первой группе элементов сравнения или факторам стоимости (зависимые корректировки), характеризующих отличие объекта оценки от аналога по параметрам сделки, то есть по условиям рынка, а сумма (1 +∑ ai Δxij) - резуль- тат процентной корректировки цены j-го аналога по второй группе факторов стоимости, характеризующих отличие объекта оценки от аналога по физическим и экономическим характеристикам (независимые корректировки).

На практике при расчете стоимости объекта оценки оценщики используют следующую систему корректирующих уравнений 5:

r                   ⎛k⎞

VˆO1=P1×∏(1+aˆiΔxi1)×⎜1+∑aˆiΔxi1⎟ i=1                       ⎝     i=r+1

r⎛

VˆO2=P2×∏(1+aˆiΔxi2)×⎜1+∑aˆiΔxi2 i=1                        ⎝

r⎛

VˆOn=Pn×∏(1+aˆiΔxin)×⎜1+∑aˆiΔxin i=1                       ⎝

Здесь в отличие от системы (1) V_{O 1} ,V_{O 2} , ..., V_On - откорректированные цены аналогов или показатели стоимости объекта оценки, полученные посредством корректировки соответствующих цен его аналогов. При этом символами с «шапочкой» обозначены оценки или расчетные значения соответствующих параметров модели.

Основная идея корректировки цен аналогов достаточно проста - найти такие, не противоречащие рыночным данным значения поправок цен аналогов, которые обеспечили бы либо равенство, либо минимальный разброс показателей стоимости объекта оценки, например, от их медианного или средневзвешенного значения, которое можно принять в качестве итогового показателя рыночной стоимости объекта оценки (см. [5–7]):

n

Vˆ O = ∑ w j Vˆ Oj ,                                                                                  (3)

j =1

где w_j ( j = 1, ..., n ) – известные или рассчитанные по какому-либо правилу весовые коэффициенты.

В целом, задачу оценки объекта недвижимости можно сформулировать как задачу нелинейного программирования - найти вектор коэффициентов aˆ ₁, ..., aˆ_k , который удовлетворял бы системе ограничений:

r                    _⎛ k

⎞

⎟ , j = 1,..., n

VˆOj =Pj×∏(1+aˆiΔxij)×⎜1+∑aˆiΔxij i =1                         ⎝      i=r+1

и доставлял наименьшее значение целевой функции - дисперсии откорректированных цен аналогов:

² S_V

n - 1

n

∑ 2

Vˆ - Vˆ → min .

OOj j=1                                   a1,...,ak

Если информация о ценах аналогов одинаково надежна, разброс откорректированных значений цен небольшой, то в качестве показателя стоимости объекта оценки можно ис-

⁵ В отчетах об оценке эта система, как правило, представляется в виде таблицы или сетки корректировок.

пользовать простое среднее откорректированных цен аналогов: ⁿ

• ^V O = - Z V O .                                                                 (5)

n j =1

Система уравнений (2) записана в системе координат отклонений, каждое из которых представляет собой разность значений ценообразующих факторов объекта оценки и его аналога. При этом сам объект оценки находится в начале (центре) этой системы координат. Если ценообразующие факторы какого-либо аналога совпадут с соответствующими ценообразующими факторами объекта оценки, то стоимость последнего будет равна цене этого аналога. Из-за этой особенности система уравнений корректировок в отличие от уравнений регрессии, используемых для массовой оценки объектов недвижимости, является системой «одноразового» применения - только для одной (индивидуальной) оценки объекта, так как при смене объекта оценки изменится и система координат, в которой описаны аналоги. Однако параметры, получаемые в процессе каждой оценки, могут использоваться для анализа ценообразования на рынке оцениваемого объекта недвижимости.

Согласно приведенным ранее определениям аналоги с известными ценами Р ₁, Р ₂, …, Р_n – это гетерогенные объекты. Откорректированные цены аналогов V_{O 1} ,V_{O 2} , ...,V_On – это «цены» гомогенных или квазигомогенных объектов. В целом, систему (2) можно определить как систему уравнений корректировки цен аналогов или гомогенизации выборки гетерогенных объектов, а результат, получаемый по формуле (3) или (5), можно рассматривать в качестве оценки или показателя рыночной стоимости объекта оценки.

Учитывая нелинейность системы (2), сформулированная задача, как уже отмечалось, является задачей нелинейного программирования, для которой не всегда удается найти единственное решение.

Из системы (2) следует, что значения корректирующих коэффициентов зависят от выборки аналогов и значений ценообразующих факторов. То есть каждому новому набору аналогов будут соответствовать другие значения корректирующих коэффициентов, как это происходит и при индивидуальной оценке объектов недвижимости в рамках сравнительного подхода. Это значит, что искомое значение рыночной стоимости целиком и полностью будет зависеть от корректности («рыночности») значений цен аналогов, а предлагаемый подход, по сути, представляет собой формализованную версию классического метода корректировок сравнительного подхода.

Качество корректировок или оценки объекта недвижимости можно проверить, используя следующие показатели:

• •    CV P = S p p - коэффициент вариации исходных цен, где S p - дисперсия исходных цен;

• •    CV_V = S V/ V O - коэффициент вариации откорректированных цен, где S V - дисперсия откорректированных цен;

1 ⁿ

• •    5 = Z ( V_O — V_Oj ) V_O - среднее относительное отклонение показателей стоимости от n ,=1

среднего значения.

Теоретически коэффициент вариации откорректированных цен должен быть равен нулю. На практике же по известным причинам, а именно из-за действия различных по-грешных факторов, ошибок спецификации моделей корректировок и ошибок в процессе измерения факторов стоимости, достичь этого не удается.

Система уравнений (1) состоит из n уравнений и (k + 1) неизвестных: a1, a2, …, ak, VO. В соответствии с приведенными определениями при n > (k + 1) мы имеем переопределен- ную систему (число уравнений больше числа неизвестных), при n = (к + 1) - определенную систему (число уравнений равно числу неизвестных) и при n < (к + 1) - неопределенную или недоопределенную систему (число уравнений меньше числа неизвестных).

В любом случае для нелинейных систем поиск аналитического решения задачи оценки (если оно существует) связан со значительными трудностями вычислительного характера. Для них также сложно аналитически доказать существование и единственность решений. В лучшем случае для нелинейных систем можно установить, что найденное решение является точкой локального экстремума (максимума или минимума) целевой функции. Доказать же, что эта точка является точкой глобального экстремума, можно только посредством исследования результата в области всех возможных решений или анализа полученного результата на предмет здравого смысла посредством сравнения результата оценки объекта недвижимости с ценами его рыночных аналогов.

Разность v = ( к + 1 - n ) есть число степеней свободы системы уравнений корректировок. Забегая вперед, отмечу, что при v <  0 система имеет единственное решение, при v >  0 - множество решений.

Проанализируем возможности численного решения задач оценки объектов недвижимости для указанных вариантов систем в порядке их перечисления.

Оценка стоимости объекта недвижимости в случае переопределенной системы уравнений

Пример 1

Объектом оценки является нежилое помещение площадью 40 квадратных метров на правах собственности, находящееся в центре некоего поселения. В процессе оценки подобраны 7 аналогов (см. табл. 1), находящихся на разном расстоянии от центра поселения (далее – РЦП). В таблице 2 представлено описание объекта оценки и его аналогов в цифровом виде 6. При этом право собственности обозначено цифрой 2, а право аренды – цифрой 1.

Таблица 1

Качественное описание помещений

Параметр	Объект оценки (О) и объекты-аналоги (А)
	О	A 1	A 2	A 3	A 4	A 5	A 6	A 7
Удельная цена, д. е. за м2	?	110 000	140 000	60 000	90 000	60 000	90 000	70 000
Право	собственность			аренда	собственность	аренда	собственность	аренда
Площадь, м2	40	40	50	200	50	180	40	200
РЦП, м	0	500	0	1 500	1 000	1 500	1 000	1 000

Корректность подбора аналогов и корректность оцифровки качественных факторов можно проверить посредством анализа данных таблицы 2 на предмет соответствия рыночным тенденциям знаков и значений коэффициентов корреляции:

• •    права – 0,811;

Таблица 2

Цифровое описание помещений

Параметр	Объект (О) оценки и объекты-аналоги (А)
	О	A 1	A 2	A 3	A 4	A 5	A 6	A 7
Удельная цена, д. е. за м2	?	110 000	140 000	60 000	90 000	60 000	90 000	70 000
Право	2			1	2	1	2	1
Площадь, кв. м	40	40	50	200	50	180	40	200
РЦП, м	0	500	0	1 500	1 000	1 500	1 000	1 000

• •    площадь помещения – -0,791;

• •    РЦП – -0,972.

Отсюда, например, следует, что между ценой и площадью существует тесная обратная связь. Это значит, что с ростом площади помещения его удельная цена уменьшается, что, как правило, характерно для рынка недвижимости. Та же вполне закономерная зависимость существует между ценой и расстоянием до центра поселения – по мере удаления от центра удельная цена падает. Важно отметить, что нелогичность знаков коэффициентов корреляции может свидетельствовать:

• 1)    о некорректном подборе аналогов;

• 2)    о неверной информации о ценах;

• 3)    о неправильной оцифровке качественных факторов стоимости.

В таблице 3 представлен расчет разностей значений ценообразующих факторов объекта оценки и его аналогов по формуле:

Δxij = (xij – xi0), где i – номер ценообразующего фактора;

j – номер аналога.

Этой формулой описываются объект оценки и его аналоги в системе координат отклонений ценообразующих факторов аналогов от соответствующих факторов объекта оценки.

Таблица 3

Описание помещений в системе координат отклонений

Параметр	Объект оценки (О) и объекты-аналоги (А)
	О	A 1	A 2	A 3	A 4	A 5	A 6	A 7
Удельная цена, д. е. за м2	?	110 000	140 000	60 000	90 000	60 000	90 000	70 000
Право ( x 1)	2			1	2	1	2	1
Δ x 1 j = ( x 1 j – x 1 O )	0			-1	0	-1	0	-1
Площадь ( x 2), м2	40		50	200	50	180	40	200
Δ x 2 j = ( x 2 j – x 2 O )	0		10	160	10	140	0	160
РЦП ( x 3), м	0	500	0	1 500	1 000	1 500	1 000	1 000
Δ x 3 j = ( x 3 j – x 3 O )	0	500	0	1 500	1 000	1 500	1 000	1 000

Сопоставим таблице 4 систему уравнений корректировок цен аналогов (2):

V O 1 = P 1 x ( 1 + a 1 A x 1 1 ) x ( 1 + a 2 A x 21 + a ₃ A x 31 )

V O2 = P 2 ^X( 1 + ^a 1 A x 12 ) x ( 1 + a 2 A x 22

+ a 3 A x 32 )

.

...

V O 7 = P 7 x ( 1 + a 1 A x ₁₇ ) x ( 1 + a 2 A x 27

^{+ a} 3 ^{A x} 37 )

Здесь n = 7, k = 3 и n >  ( k + 1), следовательно, мы имеем переопределенную на 3 уравнения систему. Расчеты показывают, что в этом случае при разных начальных значениях искомых коэффициентов мы приходим к одному и тому же результату оценки стоимости.

Таблица 4

Таблица корректировок (поправок) цен и расчета стоимости объекта оценки

Параметр		Объект оценки (О) и объекты-аналоги (А)
		О	А 1	А 2	А 3	А 4	А 5	А 6	А 7
Удельная цена, д. е. за м2		?	110 000	140 000	60 000	90 000	60 000	90 000	70 000
Корректировка по правам	д. е.	–	0		13930	0	13930	0	16252
	%	–	0,00		23,22	0,00	23,22	0,00	23,22
Откорректированная цена		–	110 000	140 000	73 930	90 000	73 930	90 000	86 252
Корректировка по площади	д. е.	–	0	600	5066	385	4433	0	5910
	%	–	0,00	0,43	6,85	0,43	6,00	0,00	6,85
Корректировка по РЦП	д. е.	–	30 763	0,0000	62 026	50 339	62 026	50 339	48 242
	%	–	27,97	0,00	83,90	55,93	83,90	55,93	55.93
Сумма корректировок по двум группам	%	–	27,97	0,43	90,75	56,36	89,89	55,93	62,78
	д. е.	–	30 763	600	67 092	50 724	66 459	50 339	54 153
Откорректированная цена, д. е. за м2		–	140 763	140 600	141 022	140 724	140 389	140 339	140 405
Средняя откорректированная цена (стоимость О), д. е. за м2		140 606

Статистические характеристики числового ряда откорректированных цен

Среднее квадратическое отклонение	249
Коэффициент вариации, %	0,18
Среднее относительное отклонение, %	0,14
a 1, %	-23,22
a 2, %	0,043
a 3, %	0,056
Дисперсия	61 800

В таблице 4 с использованием данных об отклонениях ценообразующих факторов из таблицы 3 представлены результаты расчета поправок цен и стоимости объекта оценки методом подбора коэффициентов коррекции aˆ1,aˆ2,aˆ3 при нулевых стартовых значениях последних 7.

Отдельное уравнение корректировки с учетом найденных значений параметров aˆ ₁, aˆ ₂, aˆ ₃ можно записать следующим образом:

V O = P j ( 1 - 0 , 2322 A x 1j ) x ( 1 + 0 , 00043 A x _{2 j} + 0 , 00056 A x _{3 j} ) . (7)

Следует отметить, что здесь и далее разность значений факторов A x j = ( x j - x 0 ₀₀) в процессе оценки рассчитывается таким образом, что знаки коэффициентов коррекции должны быть равны обратным знакам соответствующих коэффициентов корреляции: sign( a_i ) = -sign( r_i ), i = 1, 2, 3, что соответствует общему правилу корректировок цен аналогов, а именно если ценообразующий фактор аналога хуже соответствующего ценообразующего фактора объекта оценки, то цена аналога корректируется в сторону увеличения, и наоборот. Невыполнение этого условия может свидетельствовать о некорректном решении задачи оценки.

В таблице 4 показан итоговый результат решения задачи оценки объекта недвижимости - удельная стоимость помещения V O = 140 606 д. е. за один квадратный метр и значение целевой функции S V = 61 800, при которой он достигнут. Умножив удельную стоимость на площадь помещения, после округления получим оценку стоимости помещения в сумме 5 620 000 д. е.

На рисунке 1 представлена динамика изменения показателя стоимости объекта оценки в зависимости от удаления от центра поселения. На рисунке видно, что здесь имеет место нелинейная зависимость - по мере удаления от центра скорость уменьшения стоимости падает.

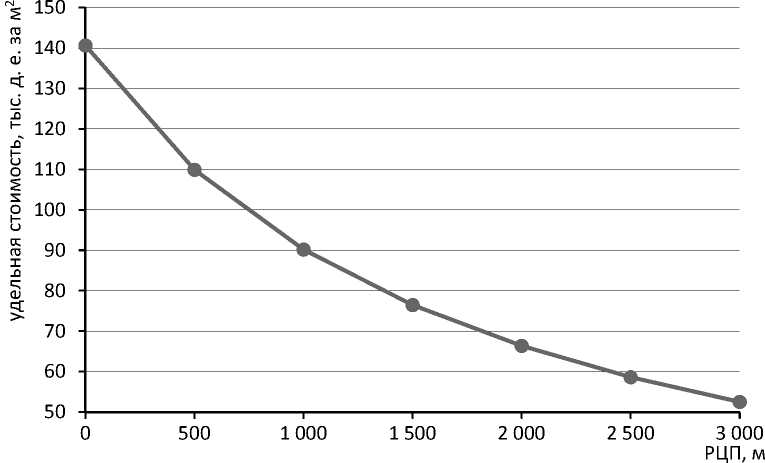
Рис. 1. Изменение показателя удельной стоимости объекта оценки от расстояния до центра поселения

Данные, приведенные в таблице 4, демонстрируют близость откорректированных значений цен аналогов, что позволяет в качестве точечного значения стоимости взять их простое среднее и не задумываться об интервале неопределенности.

Если показатели стоимости объекта оценки после окончания корректировок цен аналогов будут значимо отличаться друг от друга, то можно рассчитать доверительный интервал, в котором может находиться искомое точечное значение рыночной стоимости V_O объекта оценки. Для этого можно использовать формулу расчета доверительного интервала среднего значения ряда откорректированных цен:

./ _ ta,n -1 ^X S y    . ,            t a,n -1 ^X S y

V O      I—   <  V O <  V O +    /—

.

n

n

Для условий нашей задачи выборочное среднее или оценка удельной стоимости V O = 140 606 д. е., исправленное СКО s_y = V п/(п - 1 ) x 249 = 290 , количество аналогов (наблюдений) n = 7 . При уровне значимости a = 5% t -критерий t _{5%,(7 – 1)} равен 2,45. Отсюда получаем, что значение удельной стоимости V_O объекта оценки с 95-процентной надежностью находится в достаточно узком диапазоне – от 140 337 до 140 874 д. е.

В таблице 5 представлены значения корректировок цен аналогов в процентах и денежных единицах .

Таблица 5

Значения корректировок цен аналогов

Формула корректировки	Объекты-аналоги
	A 1	A 2	A 3	A 4	A 5	A 6	A 7
а 1 х д % 1 j , %	0,00	0,00	23,22	0,00	23,22	0,00	23,22
а 1 х д х 1 х p j , д. е.	0	0	13 930	0	13 930	0	16 252
а 2 х д х 2 j , %	0,00	0,43	6,85	0,43	6,00	0,00	6,85
а 2 х д х 2 j х p j , д. е.	0	600	5 066	385	4 433	0	5 910
а 3 х д х3 j , -%	27,97	0,00	83,90	55,93	83,90	55,93	55,93
а з х д х 3 j х P j , д. е.	30 763	0,0000	62 026	50 339	62 026	50 339	48 242

Из таблицы 5 видно, что вклады в стоимость объекта оценки при корректировке цен разных аналогов в денежных единицах разные. Так, например, изменение фактора «право» с аренды на собственность для третьего аналога приводит к корректировке его цены на 13 930 д. е., а для седьмого – на 16 252 д. е.

Одним из критериев качества выполненной оценки может служить характер распределения отклонений отдельных показателей стоимости объекта оценки У_о 1 ,У_{О 2} ,...,У_Оп от итогового показателя стоимости V_O . Распределение отклонений должно быть без каких-либо выбросов с относительно низким стандартным отклонением. Это распределение можно использовать для изучения аналогов и их цен на предмет их однородности с объектом оценки.

Как уже отмечалось, решение задачи оценки объекта недвижимости в сформулированной постановке представляет собой процесс гомогенизации выборки гетерогенных объектов. Главная цель этого процесса – получить выборку показателей стоимости объекта оценки с минимальным разбросом вокруг среднего.

В качестве показателей качества выполненной оценки в дополнение к перечисленным можно использовать следующие:

• •    дисперсия на входе в задачу корректировки и на выходе;

• •    размах исходных и откорректированных цен с низким стандартным отклонением;

• •    коэффициент осцилляции, который характеризует разброс крайних значений цен аналогов от их средних значений до и после корректировок;

• •    коэффициент вариации, который характеризует степень вариабельности цен аналогов до и после корректировок;

• •    соответствие знаков и значений коэффициентов коррекции a_i , i = 1, …, k рынку и здравому смыслу.

Коэффициент вариации цен аналогов после корректировок позволяет получить информацию о разбросе показателей стоимости объекта оценки по окончании итерационного процесса. В таблице 6 представлены показатели качества выполненной оценки.

Таблица 6

Показатели качества корректировок цен аналогов

Показатель		Цена
		исходная	откорректированная
Стандартное отклонение		29 114	249
Размах цен		80 000	683
Коэффициент	осцилляции, %	90,3	0,49
	вариации, %	32,9	0,117

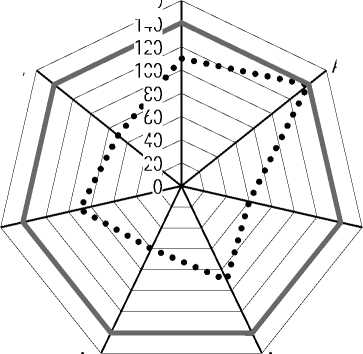
В нашем случае размах исходных цен (см. табл. 4) равен 140 0000 – 60 000 = 80 000 д. е. Размах же откорректированных цен составил 141 022 – 140 339 = 683 д. е. Показатели вариации свидетельствуют о близости показателей стоимости объекта оценки – коэффициенты осцилляции и вариации в процессе корректировок уменьшились на порядки. Отклонения откорректированных цен от стоимости объекта оценки в процентах невелики (см. рис. 2). Основная доля разности цен аналогов объясняется разными правами. На рисунке 3 представлена лепестковая диаграмма распределения цен аналогов и показателей стоимости. Диаграмма показывает, что наименьшей корректировке подверглась цена второго аналога. Это обусловлено тем, что значения его ценообразующих факторов наиболее близки к значениям ценообразующих факторов объекта оценки, а его цена, как следствие этого, наиболее близка к стоимости объекта оценки.

Необходимо еще раз отметить важность четвертого показателя качества выполненной оценки - содержательная экономическая интерпретация найденных коэффициентов. Величины и их знаки коэффициентов определяются в процессе решения системы уравнений и целиком и полностью зависят от цен и факторов, входящих в эту систему. Значения этих коэффициентов, противоречащих экономике и здравому смыслу, могут быть результатом использования для оценки аналогов, цены которых противоречат логике рыночного ценообразования. Например, большой разброс цен двух аналогов при небольшой разнице значений ценообразующих факторов может привести к тому, что решение будет получено, но система уравнений будет несбалансированной, то есть цены аналогов, ценообразующие факторы и знаки коэффициентов не будут с точки зрения рынка соответствовать друг другу.

Одной из сложных проблем решения нелинейных уравнений является проблема выбора начальных значений искомых параметров. Абсолютно надежных методов выбора начальных значений не существует. На практике при их выборе обычно руководствуются

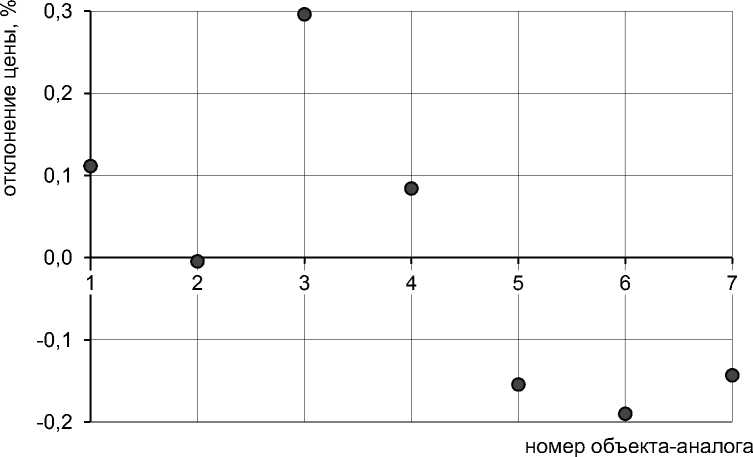
Рис. 2. Распределение отклонений откорректированных удельных цен объектов-аналогов от показателя удельной стоимости объекта оценки

А7

А 2

А1

160 140

А б

А з

А5

А4

.....цены откорректированные цены

Рис. 3. Лепестковая диаграмма распределения цен объектов-аналогов и их откорректированных значений (стоимостей), в тыс. д. е.

информацией из предметной области исследуемого явления. При отсутствии априорной информации о процессах ценообразования можно попытаться выбрать начальные условия, например, методом «грубой силы» 8.

В нашем случае в качестве начальных выбраны нулевые значения искомых параметров. При этом в начале итерационного цикла рассчитываемая стоимость оказалась равной среднему значению цен аналогов, которое можно расценивать в качестве первого приближения к ее искомому значению, не выходящему за границу множества цен аналогов. Известно, что основная трудность решения задач нелинейного программирования состоит в том, что эти задачи часто являются многоэкстремальными и известные чис- ленные методы их решения гарантируют в общем случае сходимость минимизирующих последовательностей лишь к точкам локальных экстремумов. Вывод же о глобальности найденного экстремума можно сделать, проанализировав полученный результат, опираясь на здравый смысл.

Для того чтобы убедиться в том, что найденное решение является стационарной точкой целевой функции, следует проанализировать, как меняется ее значение при определенных изменениях найденных значений коэффициентов коррекции (см. табл. 7 и рис. 4).

Таблица 7

Зависимость значений целевой функции от изменения коэффициентов коррекции

Изменение значений коэффициентов, %		-20	-10	0	+10	+20
Значение целевой функции (дисперсии)	а 1	8 083 922	2 067 304	61 801	2 067 304	8 083 922
	а 2	344 115	132 388	61 801	132 352	344 042
	а 3	19 107 829	4 823 342	61 801	4 823 206	19 107 559

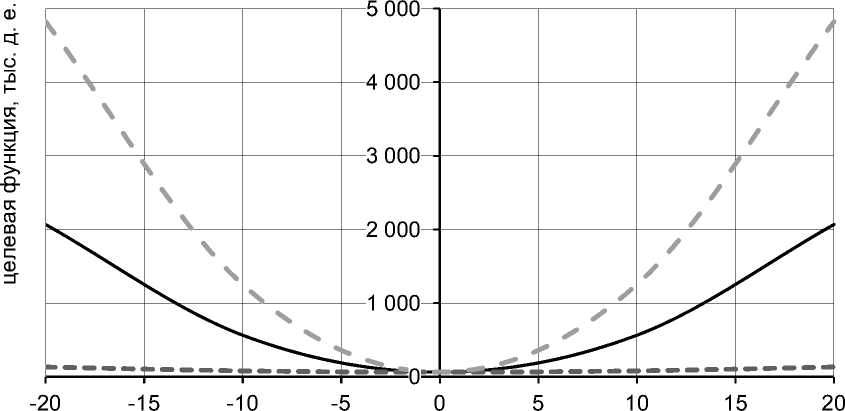
коэффициент коррекции, %

DA 1--- DA 2-- DA 3

Рис. 4. Зависимость значений целевой функции от коэффициентов коррекции

Из данных таблицы 7 и рисунка 4 следует, что при отклонении коэффициентов коррекции от экстремальных значений как в минус, так и в плюс дисперсия возрастает. Это указывает на то, что найденные значения коэффициентов коррекции соответствуют стационарной точке в области допустимых решений.

Далее необходимо проанализировать полученное значение рыночной стоимости на предмет соответствия рыночным данным посредством сравнения этого значения с ценами аналогов. Так, например, из таблицы 3 следует, что площадь объекта оценки на 10 квадратных метров меньше площади второго аналога. Эта разность обеспечила более высокую удельную стоимость объекта оценки (140 606 д. е. против 140 000 д. е.), что соответствует здравому смыслу.

Для проверки работоспособности предлагаемого алгоритма выполним расчет стоимости каждого из объектов-аналогов (см. табл. 8).

Таблица 8

Оценка стоимости объектов-аналогов

Параметр	Объекты-аналоги
	A 1	A 2	A 3	A 4	A 5	A 6	A 7
Удельная цена, д. е. за м2	110 000	140 000	60 000	90 000	60 000	90 000	70 000
Удельная стоимость, д. е. за м2	109 878	140 006	59 822	89 923	60 092	90 170	70 099
a 1, %	-23,211	-23,211	-18,838	-23,203	-18,842	-23,208	-18,833
a 2, %	0,034	0,043	0,022	0,027	0,023	0,028	0,026
a 3, %	0,044	0,056	0,029	0,036	0,029	0,036	0,034
Относительная ошибка, %	0,111	0,005	0,296	0,086	0,154	0,189	0,141
Средняя относительная ошибка, %	0,14

Из данных таблицы 8 следует, что предлагаемый подход для переопределенной системы позволяет выполнить оценку стоимости выбранных аналогов с погрешностью, не превышающей долей процента. Этой же точности можно ожидать в процессе оценки любого объекта оценки, ценообразующие характеристики которого находятся внутри диапазона изменения характеристик этих аналогов.

Для того чтобы уменьшить влияние аналогов-выбросов, расчет стоимости объекта оценки можно выполнять не по формуле (5), а по формуле (3). При этом весовые коэффициенты можно рассчитывать, ориентируясь на близость каждого аналога к объекту оценки по правилу «чем ближе по характеристикам аналог к объекту оценки, тем больший вклад в стоимость объекта оценки должен внести этот аналог». Степень близости аналога к объекту оценки можно рассчитать по формуле:

k ₂ l j = ∑ ( u ij - u io ) .

i =1

Здесь u_ij - масштабированная до единичной длины i -я характеристика объекта оценки и аналогов:

uij = xijmxi, где mxi =

ma_j x ( x_ij )

-1

- масштаб i -ой характеристики.

При этом веса определяются по формуле:

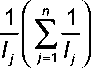
-1

Используя данные таблицы 4, по формулам (9) - (11) рассчитаем для нашей задачи веса аналогов: w ₁ = 10,6%; w ₂ = 70,6%; w ₃ = 2,6%; w ₄ = 5,3%; w ₅ = 2,7%; w ₆ = 5,3%; w ₇ = 3,1%.

Наименьшие веса имеют аналоги 3, 5 и 7, которые по характеристикам дальше всех от объекта оценки. Используя полученные веса, рассчитаем итоговую стоимость по формуле (3):

V O = 140 763 X 0,106 + 140 600 x 0,706 + 141 022 x 0,026 + 140 724 x 0,053 +140 389 x X 0,027 + 140 339 X 0,053 + 140 405 x 0,031 = 140 609 д. е.

Надо отметить, что l_j - это расстояние в k -мерном евклидовом нормированном пространстве между j -м аналогом и объектом оценки. Расстояние между ними может равняться нулю только в случае полного совпадения характеристик j -го аналога и объекта оценки. Такой аналог будет иметь 100-процентный вес, а стоимость объекта оценки будет равна цене этого аналога.

Окончание в следующем номере журнала.

***

P^^^^ Единый

I                < ресурс

^^^~ ^™ I застройщиков

С ДЕКАБРЯ В КВАРТИРАХ МОЖНО РАЗМЕЩАТЬ БАНИ И САУНЫ

С 1 декабря 2022 года вступили в действие изменения №3 к своду правил СП 4.13130.2013 «Системы противопожарной защиты. Ограничение распространения пожара на объектах защиты. Требования к объемно-планировочным и конструктивным решениям» утвержденные приказом МЧС России №610 от 15.06.2022. Напомним, что применение СП 4.13130.2013 обеспечивает соблюдение требований к объемно-планировочным и конструктивным решениям по ограничению распространения пожара в зданиях и сооружениях, установленных 123-ФЗ.

В новой редакции исключено положение, о том, что СП применяется при эксплуатации здания. В СП актуализировано большинство нормативных ссылок на стандарты и своды правил. Кроме того, СП дополнен новыми положениями, устанавливающими противопожарные расстояния от жилых и общественных зданий, сооружений до открытых площадок для стоянки автомобилей. Также в документе откорректированы положения, устанавливающие противопожарные расстояния до границ лесных насаждений от зданий, сооружений городских населенных пунктов в зонах индивидуальной и малоэтажной жилой застройки, от зданий и сооружений сельских населенных пунктов. Также внесены изменения, касающиеся проектирования зданий класса Ф1.3 с встроенными

Окончание на с. 46