Применение численного метода для расчета корректировок цен объектов-аналогов в рамках сравнительного подхода

Оценка стоимости объекта недвижимости в случае определенной системы уравнений корректировок

Пример 2

Рассмотрим решение задачи оценки помещения, используя данные примера 1, только без трех последних аналогов (см. таблицы 1 и 9).

В таблице 10 данные представлены в цифровом виде в системе координат ценообразующих факторов (далее также – ЦОФ).

Таблица 9

Качественное описание помещений

Параметр	Объект оценки (О) и объекты-аналоги (А)
	О	A 1	A 2	A 3	A 4
Удельная цена, д. е. за м2	???	110 000	140 000	60 000	90 000
Права	собственность			аренда	собственность
Площадь, м2	40	40	50	200	50
РЦП, м	0	500	0	1 500	1 000

Таблица 10

Цифровое описание помещений

Параметр	Объект оценки (О) и объекты-аналоги (А)
	О	A 1	A 2	A 3	A 4
Удельная цена, д. е. за м2	???	110 000	140 000	60 000	90 000
Права	2			1	2
Площадь, м2	40	40	50	200	50
РЦП, м	0	500	0	1 500	1 000

* о кончание . н ачало см. и мущественные отношения в р оссийской ф едерации . 2023. № 4.

На предварительном этапе, как и в предыдущем примере, корректность подбора аналогов и корректность кодировки ценообразующих факторов проверяется посредством анализа знаков и значений коэффициентов корреляции на предмет проверки знаков связи между зависимой и независимыми переменными и соответствия рыночным тенденциям, которую можно получить, используя данные таблицы 10. Как видно, после удаления трех аналогов корреляция осталось практически такой же:

• •    права – 0,792;

• •    площадь помещения – -0,786;

• •    РЦП – -0,997.

В таблице 11 объект оценки и его аналоги представлены в системе координат отклонений.

Таблица 11

Описание помещений в системе координат отклонений

Параметр	Объект оценки (О) и объекты-аналоги (А)
	О	A 1	A 2	A 3	A 4
Удельная цена, д. е. за м2	???	110 000	140 000	60 000	90 000
Права ( x 1)	2			1	2
Δ x 1 j = ( x 1 j – x 1 O )	0			-1	0
Площадь ( x 2), м2	40	40	50	200	50
Δ x 2 j = ( x 2 j – x 2 O )	0	0	10	160	10
РЦП ( x 3), м	0	500	0	1 500	1 000
Δ x 3 j = ( x 3 j – x 3 O )	0	500	0	1 500	1 000

Из таблицы видно, что объект оценки находится в начале такой системы координат:

• ^{A x} 1 0 = ^{A x} 2 O = A x 3 O = 0.

Систему уравнений корректировок можно представить таким образом:

^VO 1 — P ( 1 + a ₁ ^A x 11 ) X ( 1 + a 2 ^A x 21 + a 3 ^{A x} 31 )

V O 2 — P 2 ( 1 + a ₁ A x ₁₂ ) x ( 1 + a 2 A x ₂₂ + a 3 A x 32 )

V O 3 ^— P 3 ^{( 1 +} a 1 ^A x 13 ) ^{X ( 1 +} a 2 ^{A x} 23 ⁺ a 3 ^{A x} 33 ) _ V o 4 — P 4 ( 1 + a 1 A x 14 ) x ( 1 + a , A x 24 + a i A x 34 )

Здесь a ₁, a 2 , a ₃ - оценки искомых корректирующих коэффициентов.

В системе (12) n = 4 , k = 3 , то есть n = ( k + 1), и мы имеем определенную систему. Расчеты показывают, что и в этом случае при разных начальных значениях искомых коэффициентов мы приходим к одному и тому же результату. В таблице 12 представлены результаты расчета стоимости методом подбора коэффициентов коррекции aˆ ₁, aˆ ₂, aˆ ₃ при их нулевых стартовых значениях, полученные с помощью программы «Поиск решений» из библиотеки MS Excel, с учетом данных по отклонениям ЦОФ из таблицы 11.

Отдельное уравнение корректировок с учетом найденных значений параметров можно представить следующим образом:

V_Q = P (1 - 0 , 22 A x ,, ) х (1 + 0 , 00051 A x ₂, + 0 , 00056 A x ₃,) . Oj j                          ¹ j                                       ² j                              ³ j

Таблица 12

Таблица корректировок (поправок) цен и расчета стоимости объекта оценки

Параметр	Объект оценки (О) и объекты-аналоги (А)
	О	A 1	A 2	A 3	A 4
Удельная цена, д. е. за м2	???	110 000	140 000	60 000	90 000
Поправка по 1-й группе ЦОФ по правам, д. е.	–	0		13 333	0
Откорректированная удельная цена, д. е. за м2	–	110 000	140 000	73 333	90 000
1-я поправка по 2-й группе ЦОФ по площади, %	–	0,00	0,51	8,12	0,51
2-я поправка по 2-й группе ЦОФ по РЦП, %	–	27,92	0,00	83,76	55,84
Суммарная поправка по 2-й группе ЦОФ, %	–	27,92	0,51	91,88	56,35
Откорректированная удельная цена, д. е. за м2	–	140 711	140 711	140 711	140 711
Средняя откорректированная цена (стоимость О), д. е. за м2	140 711
Дисперсия	7,7 х 10-8

В таблице 12 показан итоговый результат - удельная стоимость помещения V O = 140 711 д. е. за квадратный метр и значение целевой функции S V = 7,7 х 10^-8, при которой он достигнут. Умножив удельную стоимость на площадь помещения, после округления получим оценку стоимости помещения в сумме 5 630 000 д. е.

Мы рассмотрели задачу оценки стоимости объекта недвижимости, предусматривающую корректировку цен аналогов как по первой, так и по второй группе факторов стоимости. На практике часто корректировки по первой группе, состоящей из r элементов сравнения, так называемых рыночных корректировок, выполняются в д. е. на основе использования заранее подготовленной и проверенной информации, получаемой, например, из документов, сопровождающих сделку. В этом случае уравнение корректировки цены отдельного аналога можно записать в следующем виде:

( к

1 + Ё a , A x j i = r +1

где P 1 = P j + Ё A/ = > - откорректированное по 1 группе значение цены j -го аналога факторов;            ⁱ=¹

P _j – исходная цена аналога, причем j = 1, …, n.

То есть неизвестными остаются k – r коэффициентов коррекции. Тогда систему уравнений корректировок можно записать так:

V 1 = P _п |1 + £ < iA x „'

I ⁱ =¹ J

(       ˆ _⎛ k - r          _⎞

V O 2 = ^P 12 I ^{1 +} ^ a i ^A x i 2

I      ⁱ=^{1           J}

..

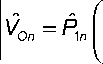
• 1    + £ a A x n

Раскроем скобки:

ˆ

V O 1

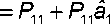
ˆ

ˆ

+ ^Pii 8 2 ^{A x} 21 ⁺ ... ^{+ P}ii^ak - r ^{A x} ( k - r ) 1

^

V o 2

^

= R

+ P ₁₂ a₁ A x ₁₂

Л                        Л

^{+ P} 12 a 2 ^A x 22 ⁺ ". ^{+ P} 12 a k - r ^A x ( k - r ) 2

.

ˆˆˆ    ˆ     ˆ

V On = ^P 1 n ^{+ P} 1 n a 1^1 n ^{+ P} 1 n a 2 ^A x 2 n ⁺ ■■■ ^{+ P} 1 n a k - r \ x ( k - r ) n

Допустим, мы подобрали такие корректирующие коэффициенты, что все поправки приведут к одному результату V_Oj = V_O для любого j = 1, …, n . Тогда систему уравнений (15) можно записать так:

^

VˆO

- P₁₁a₁ A x .

-

^P 11 a 2 A x 21

^- ... ^- Pa - r \ x ( k - r ) 1

л

= R

= 11

ˆ

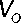
- P ₁₂ a ₁ A x ₁₂

P 12 a 2 \ x 22    ...   ^P 12 a k - r \ x ( k - r ) 2 = ^P 12

ˆˆ       ˆ          ˆ          ˆ

V O ^{- P} 1 n a 1 \ x 1 n ^{- P} 1 n a 2 \ x 2 n ^- ... ^{- P} 1 n a k - r \ x ( k - r ) n = ^P 1 n

Система (16) есть система n линейных уравнений с ( k-r + 1) неизвестными:

V O , a 1 , • • • , a k - r .

Для удобства представим ее в матричном виде:

A P x A = P ,                                                                       (17)

где A P _n ( _{k—r +} 1) - матрица системы, каждый элемент которой равен P_1j A x j : A P j = P_1j A x ij;

A _{( k – r + 1)} – матрица-столбец искомых параметров;

P _n – матрица-столбец известных цен аналогов:

	1	ˆ -A P 11
	1	ˆ - A P 21
Δ P =

-A P n 1

A =

Л

Vˆ O

Л a1

P 1

и

P =

P 2

...

a k - r

P n

Пусть n = k - r + 1 и матрица системы A P является обратимой, тогда система (17) имеет единственное решение:

A = a Р1 х р .

Первым элементом матрицы-столбца А является искомая оценка удельной стоимости V_O объекта оценки. Другие элементы матрицы-столбца А - искомые коэффициенты коррекции цен аналогов: a 1 ,..., a_k - _r .

Рассмотрим пример решения задачи, представленной в примере 2, с использованием формулы (18).

Для этого предположим, что ценообразующий фактор «права» относится ко второй группе элементов сравнения и, используя данные таблицы 11, составим матрицу системы:

1 , 00 E + 00 0 , 00 E + 00   0 , 00 E + 00 1 , 00 E + 00 0 , 00 E + 00 - 1 , 40 E + 06 A P = 1 , 00 E + 00 6 , 00 E + 04 - 9 , 60 E + 06 1 , 00 E + 00 0 , 00 E + 00 - 9 , 00 E + 05

- 5 , 50 E + 07 0 , 00 E + 00 - 9 , 00 E + 07 - 9 , 00 E + 07

Найдем для нее обратную матрицу:

	1 , 28 E + 00   5 , 03 E - 01 0 , 00 E + 00 - 7 , 82 E - 01
( A P )" ’ =	1 , 32 E - 04 - 5 , 15 E - 05 1 , 67 E - 05 - 9 , 76 E - 05 9 , 14 E - 07 - 3 , 55 E - 07 0 , 00 E + 00 - 5 , 58 E - 07 5 , 08 E - 09   9 , 14 E - 09 0 , 00 E + 00 - 1 , 42 E - 08

Теперь по формуле (18) вычислим искомую матрицу-вектор A :

1 , 28 E + 00

1 , 32 E - 04

9 , 14 E - 07

5 , 08 E - 09

5 , 03 E - 01

- 5 , 15 E - 05

- 3 , 55 E - 07

9 , 14 E - 09

0 , 00 E + 00

1 , 67 E - 05

0 , 00 E + 00

0 , 00 E + 00

- 7 , 82 E - 01

- 9 , 76 E - 05

- 5 , 58 E - 07

- 1 , 42 E - 08

110 000

140 000

60 000

90 000

140 711

- 42 , 6 % 0 , 051 %

0 , 056 %

Первым элементом матрицы столбца А является показатель стоимости объекта оценки 140 711 д. е. за один квадратный метр. Второй, третий и четвертый элементы матицы столбца А - коэффициенты коррекции цен аналогов. Произведение цены аналога на коэффициент коррекции равно вкладу единицы соответствующего фактора стоимости в стоимость объекта оценки.

Таким образом, отсутствие необходимости выполнения корректировок по первой группе факторов стоимости при условии n = k – r + 1 позволяет получить точное аналитическое решение системы уравнений оценки объекта недвижимости с применением сравнительного подхода.

Расчеты показывают, что практически такой же результат получается при итерационном решении этой задачи (см. табл. 13) по уравнениям (14) при нулевых стартовых значениях коэффициентов коррекции.

Таблица 13

Расчет стоимости объекта оценки

Параметр		Объект оценки (О) и объекты-аналоги (А)
		О	A 1	A 2	A 3	A 4
Поправка по	х 1	–	0	0	25 586	0
	x 2	–	0	710	4 871	457
	x 3	–	30 711	0.00	50 254	50 254
Откорректированная удельная цена, д. е. за м2		–	140 711	140 710
Средняя откорректированная цена (стоимость О), д. е. за м2		140 710
Дисперсия		1,58 x 10 -2
a 1, %		42,643
a 2, %		0,051
a 3, %		0,056

Коэффициенты коррекции при нулевых стартовых значениях в конце итерационного процесса приняли следующие значения:

а 1 = -42,7%;

a ₂ = +0,051%;

a ₃ = +0,056%.

Общая стоимость помещения округленно равна:

140 711 x 40 = 5 630 000 д. е.

Следует отметить, что совпадение итерационного и аналитического решений свидетельствует о возможности выбора в качестве начальных нулевых значений коэффициентов коррекции цен аналогов.

Оценка стоимости объекта недвижимости в случае недоопределенной системы уравнений

Пример 3

Рассмотрим решение задачи оценки помещения, используя данные примера 2, исключив для этого из него еще один аналог (см. табл. 9). В этом случае объект может быть описан так, как показано в таблице 14.

Таблица 14

Качественное описание помещений

Параметр	Объект оценки (О) и объекты-аналоги (А)
	О	A 1	A 2	A 3
Удельная цена, д. е. за м2	???	110 000	140 000	60 000

Права	собственность			аренда
Площадь, м2	40		50	200
РЦП, м	0	500	0	1 500

Представим описание объекта в отклонениях ценообразующих факторов объектов-аналогов от таковых объекта оценки (см. табл. 15).

Таблица 15

Описание помещений в системе координат отклонений ЦОФ

Параметр	Объект оценки (О) и объекты-аналоги (А)
	О	A 1	A 2	A 3
Удельная цена, д. е. за м2	???	110 000	140 000	60 000
Права ( х 1)	2			1
Δ x 1 j = ( x 1 j – x 1 O )	0			-1
Площадь ( х 2), м2	40		50	200
Δ x 2 j = ( x 2 j – x 2 O )	0		10	160
РЦП ( х 3), м	0	500	0	1 500
Δ x 3 j = ( x 3 j – x 3 O )	0	500	0	1 500

Решим эту задачу, как и ранее, подбором параметров, которых здесь три – aˆ ₁, aˆ ₂, aˆ ₃ . Анализ знаков и величин коэффициентов корреляции соответствует рыночным тенденциям, и между зависимой и независимыми переменными имеется очень сильная корреляционную связь:

права – 0,92;

площадь помещения – -0,86;

РЦП – -0,999.

Запишем систему уравнений корректировок цен аналогов (2) следующим образом:

V o i = P i ( 1 + a Ax 11 ) x ( 1 + a 2 A x 2i + a 3 A x 31 )

• ^VO 2 = P 2 ( 1 + a 1 ^{A x} 12 ) X ( 1 + a 2 ^{A x} 22 + a 3 ^{A x} 32 ) .                                                     ⁽¹⁹⁾

V 3 = P 3 ( 1 + a 1 A X 13 ) x ( 1 + a 2 A x 23 + a 3 a * 33 )

Здесь n = 3, k = 3, то есть n < ( k + 1), и система не доопределена. С математической точки зрения мы имеем один свободный параметр, который может принимать любые значения, обеспечивая тем самым бесчисленность решений системы уравнений (19).

Такие системы для их решения нужно либо доопределять, например, связывать свободные (лишние) параметры дополнительными уравнениями или, что практически то же самое, присваивать им заранее определенные фиксированные значения, выводя их тем самым из разряда неизвестных.

В таблице 16 представлено решение задачи оценки стоимости объекта недвижимости посредством подбора неизвестных параметров методом последовательных приближений с учетом отклонений ЦОФ из таблицы 15. Решение получено посредством доопределения системы уравнений корректировок (19) равенством a1 = -22,23%.

Таблица 16

Таблица корректировок (поправок) цен и расчета стоимости объекта оценки

Параметр		Объект оценки (О) и объекты-аналоги (А)
		О	A 1	A 2	A 3
Поправка по 1-й группе ЦОФ по правам, д. е.	д. е.	–	0		13 341
	%	–	0,00		22,23
Откорректированная удельная цена, д. е. за м2		–	110 000	140 000	73 341
1-я поправка по 2-й группе ЦОФ по площади	д. е.	–	0	709	5 944
	%	–	0,00	0,51	8,10
2-я поправка по 2-й группе ЦОФ по РЦП	д. е.	–	30 709	0,00	61 424
	%	–	27,92	0,00	83,75
Суммарная поправка по 2-й группе ЦОФ	д. е.	–	30 709	709	67 368
	%	–	27,92	0,51	91,86
Откорректированная удельная цена, д. е. за м2		–	140 709
Средняя откорректированная цена (стоимость О), д. е. за м2		140 709
Дисперсия		1,33 X 10-15

Удельная стоимость равна 140 709 д. е. Умножив ее на площадь, после округления получим оценку стоимости всего помещения в сумме 5 630 000 д. е.

В таблице 17 представлены итоговые результаты оценок для пяти систем корректирующих уравнений: 3-х переопределенных, одной определенной и одной недоопределенной.

Таблица 17

Итоговые результаты оценок рыночной стоимости объекта оценки при разном количестве объектов-аналогов

е- «в i	Система уравнений
	переопределенная				определенная	недоопределенная
	5 уравнений, 3 фактора	6 уравнений, 3 фактора	7 уравнений, 3 фактора	15 уравнений, 3 фактора	4 уравнения, 3 фактора	3 уравнения, 3 фактора
V O	5 620 000	5 610 000	5 620 000	4 669 000	5 630 000	5 620 000
a 1, %	-25,396	-25,662	-23,000	-29,21356	-22,000	-22,2
a 2, %	0,021	0,017	0,045	0,01268	0,051	0,044
a 3, %	0,056	0,056	0,056	0,03224	0,056	0,056
CKO *	168	187	242	8 167	0	0
CVv , %	0,12	0,13	0,17	7,00	0,00	0,00

* СКО – среднее квадратическое отклонение.

Из таблицы следует очевидная близость значений коэффициентов коррекции полученных результатов для разной степени определенности системы корректирующих уравне- ний, что свидетельствует об относительной инвариантности решений по поиску коэффициентов коррекции к числу аналогов и возможности использования метода для малых выборок.

В целом, алгоритм оценки стоимости объекта или объектов недвижимости предлагаемым методом можно представить в виде следующей последовательности:

• 1)    анализ ценообразующих факторов объекта оценки;

• 2)    изучение рынка объекта оценки и подбор его аналогов;

• 3)    спецификация модели оценки (определение состава и последовательности корректировок);

• 4)    проверка работы модели посредством оценки стоимости каждого аналога;

• 5)    расчет стоимости объекта недвижимости.

В этой последовательности наиболее значимыми являются этапы спецификации модели и проверки работы модели посредством оценки стоимости каждого аналога. Они необходимы для того, чтобы определить формулу корректировки объектов-аналогов и способность модели воспроизвести цены всех аналогов.

Заключение

Автором статьи рассмотрено применение численного метода для расчета корректировок (поправок) цен аналогов при использовании сравнительного подхода к индивидуальной оценке стоимости объектов недвижимости, базирующегося на действии Закона единой цены.

Метод можно использовать для оценки объектов недвижимости, если объем выборки подобранных для оценки аналогов больше или равен числу коэффициентов коррекции, увеличенному на единицу. В противном случае решение возможно лишь посредством доопределения системы – добавления аналогов в выборку или присвоения «лишним» (свободным) коэффициентам коррекции заранее определенных фиксированных значений, выводя тем самым их из разряда неизвестных.

При определенных условиях соотношения числа аналогов, вида корректировок и количества ценообразующих факторов возможно аналитическое решение систем уравнений корректировки цен аналогов.

Результат оценки стоимости объекта недвижимости полностью зависит от корректности использованной для оценки выборки его аналогов. Доказательственный результат можно получить посредством оценки объекта недвижимости на разных выборках из сегмента рынка, к которому принадлежит объект оценки.

При неправильной спецификации модели корректировок, некорректных рыночных ценах и (или) ошибках измерения значений ценообразующих факторов можно получить математическое решение, соответствующее минимуму целевой функции, но не соответствующее рынку. В связи с этим при применении рассмотренного метода, как и других методов сравнительного подхода, требуется тщательный анализ входных данных (цен аналогов и ценообразующих факторов) и результатов расчета на предмет соответствия экономическому и здравому смыслу.

Необходимо дальнейшее изучение и развитие этого метода особенно в случае использования недоопределенных систем корректирующих уравнений.

В отличие от метода регрессии, который, по сути, можно отнести к методам массовой оценки, рассмотренный метод является методом индивидуальной оценки, так как предназначен для оценки стоимости лишь одного объекта недвижимости.