Применение дважды непрерывно дифференцируемого S-сплайна
Автор: Силаев Дмитрий Алексеевич, Коротаев Дмитрий Олегович, Капустин С.В.
Рубрика: Математика
Статья в выпуске: 10 (143), 2009 года.
Бесплатный доступ
Данная работа посвящена использованию сглаживающих S-сплайнов 5-й степени. Такие сплайны являются кусочно-полиномиальной функцией, причем первые три коэффициента каждого полинома, определяются условиями гладкой склейки до второй производной включительно, а остальные три - методом наименьших квадратов. С помощью таких сплайнов строятся квадратурные формулы 6-го порядка для вычисления одно- и двухмерных интегралов, а также решается задача Дирихле для уравнения Пуассона в односвязной области. Получены соответствующие оценки сходимости.
Аппроксимация, сплайн, численные методы, квадратуры, математическая физика, метод конечных элементов
Короткий адрес: https://sciup.org/147158610
IDR: 147158610 | УДК: 517.9
Текст научной статьи Применение дважды непрерывно дифференцируемого S-сплайна
1. Дважды непрерывно дифференцируемый 5-сплайн
Рассмотрим на отрезке [а, Ь] равномерную сетку xk=a + kh, k = О,...,К, h = (b-а)/К - шаг сетки. Разобьем отрезок [а, Ь] на группы, для этого введем ещё одну равномерную сетку ^=а + 1Н, Н = mh, те Z. Таким образом, переходя из одной группы в другую, мы осуществ ляем сдвиг системы координат и рассматриваем каждый I -й полином на отрезке [О,Л]. Пусть значения приближаемой функции на этой сетке у = [у0,уъ...,ук^еRx+1. Обозначим:
множество полиномов степени п с фиксированными коэффициентами а0,ах,а2. Рассмотрим функционал:
м
Ут/+к) • к=0
В классе Pg ищется такой полином gt, который минимизирует функционал
м ф' (м) = X (м(£ + kh) - yml+k )2 min(a3, а4,..., а„)
и удовлетворяет следующим условиям:
<''.=&-.(£,-£-.) = &-,(#). 4=£АН\ 4=^_,(Н), прИ1^0,...,к-1. (1)
Здесь при / = 0 gl_1(//) = gL_x(H) есть условие периодичности 5-сплайна. Так как «;=^,(ох«:=«;(ох ^j=«7(о)/2, то условия (1) есть условия гладкой склейки двух последовательных полиномов. В непериодическом случае начальные коэффициенты а^,а^,а2 задаются начальными условиями у0,уд jJ/21. Можно предполагать, что значения заданной функции ук известны с некоторой точностью, например, они есть результаты каких-либо измерений. Будем предполагать тогда, что с уменьшением шага к будет увеличиваться точность измерения, а
Математика
именно, будем предполагать, что если периодическая функция f е С6[а,Ь] задана в узлах равномерной сетки xk=a + kh, к = О,...,К своими значениями ук, то \ук - f(xk)\ < Ch6+£, f > 0. Здесь L - число групп, на которые разбита исходная таблица значений приближаемой функции С6[а,Ь] или число полиномов, составляющих сплайн. Кроме того, здесь М+1 - количество точек осреднения, и+1 - количество точек, входящих в область определения Z-ro полинома gj, ^ - точка привязки полинома gj, М-т + 1 - число таких точек, значения которых участвуют при определении двух соседних полиномов, составляющих 5-сплайн, М >т + \. В дальнейшем степень полинома и = 5.
Определение, S-сплайном назовем функцию 5” м{х) , которая совпадает с полиномом gi(x) на отрезке ^<х< £/+1.
2. Существование и единственность S-сплайна
Теорема 1. Пусть числа т и М >3 таковы, что собственные числа матрицы U не равны корню степени L из единицы (здесь L -число полиномов, составляющих сплайн). Тогда для любой периодической функции f(x), заданной на отрезке [а,Ь] своими значениями ук в точках xk=a + kh,h = (b-a)/К, существует и единственен периодический сплайн Sm ,м№)- Для непериодического случая условия на собственные числа матрицы U не требуется.
3. Сходимость S-сплайна
Теорема 2. Пусть периодическая функция f(x)e С 6[а,Ь] и пусть выполнены предположения
\f(xk)-yk\
Пусть, кроме того, собственные числа матрицы U по модулю меньше единицы. Тогда периодический сплайн S„ м(х) с узлами на равномерной сетке имеет дефект 3 (т.е. S^м(х) еС2[а,Ь]) и для х е [а,Ь] справедливы следующие оценки:
1 ахИ
/? = 0,1,2,3,4,5; х^^ при —3,4,5 .
Аналогичные оценки справедливы и для непериодического случая.
Теорема 3. Пусть £ = т/М <£*. Тогда при достаточно малых т и больших М собственные числа матрицы устойчивости по модулю меньше единицы.
Это условие устойчивости S-сплайнов аналогично условию устойчивости для кубического случая [1]. Для случая малых значений М (при 3 < М < 20 ) в результате расчета были получены значения собственных чисел матрицы U. Оказалось, что при т/М<£* <1 все собственные числа матрицы U меньше единицы. Некоторые наиболее интересные полученные значения т и М, при которых достигаются наименьшие значения max^l и аппроксимация S-сплайнами устойчива, представлены в таблице.
4. Фундаментальный S-сплайн
Фундаментальный S-сплайн Bj(x) - это периодический или непериодический S-сплайн, построенный по данным у ^уо,/]»—,№)еК*+1 и y'oeR, y^eR вида: ^у( =бу;1,]-0,...,К^.
к
Легко видеть, что линейная комбинация ^y}Bj(x) = S(x) является S-сплайном, приближаю-7=0
щам начальные данные {y^i = 0,...,К]. Заметим, что непериодические фундаментальные сплайны дополняются сплайнами с начальными условиями у'о ,у^, принимающими значения 0 или 1.
Таблица
Собственные числа матрицы U
|
м |
М |
А |
^2 |
Аз |
max /^ |
т/М |
|
4 |
2 |
-0,008 |
-0,231-0,131/ |
-0,231+0,131/ |
0,265 |
0,25 |
|
5 |
3 |
-0,005 |
0,0549-0,201/ |
0,0549+0,201/ |
0,207 |
0,60 |
|
6 |
2 |
0,0266 |
-0,285-0,129/ |
-0,285+0,129/ |
0,312 |
0,33 |
|
6 |
3 |
-0,008 |
-0,263-0,0463/ |
-0,263+0,0463/ |
0,266 |
0,50 |
|
7 |
2 |
0,0732 |
-0,167-0,305/ |
-0,167+0,305/ |
0,347 |
0,285 |
|
7 |
4 |
-0,0069 |
-0,0737-0,214/ |
-0,0737+0,214/ |
0,226 |
0,571 |
|
7 |
6 |
0,00218 |
0,116-0,207/ |
0,116+0,207/ |
0,237 |
0,857 |
|
8 |
4 |
-0,0079 |
-0,265-0,031/ |
-0,265+0,031/ |
0,266 |
0,50 |
|
8 |
5 |
-0,00403 |
0,101-0,178/ |
0,101+0,178/ |
0,204 |
0,625 |
|
8 |
7 |
0,00180 |
-0,0466-0,229/ |
-0,0466+0,229/ |
0,233 |
0,875 |
|
9 |
5 |
-0,00734 |
-0,124-0,201/ |
-0,124+0,201/ |
0,235 |
0,555 |
|
9 |
8 |
0,00134 |
-0,205-0,118/ |
-0,205+0,118/ |
0,236 |
0,888 |
|
10 |
5 |
-0,0078 |
-0,263-0,0407/ |
-0,263+0,0407/ |
0,266 |
0,50 |
|
10 |
6 |
-0,0055 |
0,0182-0,213/ |
0,0182+0,213/ |
0,213 |
0,60 |
|
11 |
7 |
-0,00322 |
0,141-0,147/ |
0,141+0,147/ |
0,203 |
0,636 |
-
5. Одномерные квадратурные формулы 6-го порядка в
Рассмотрим интеграл ^f(x)dx. Аппроксимируем подынтегральную функцию 5-сплайном
А
сплайны в интеграл:
в в к кВ к
$S(x)dx = j^ ykBk(x)dx = ^Уь \Bk{x)dx = ^укск, А А ^=0 к=0 а ^=0
В Д-1 5 дИк где ск = ^B^x^dx^^J^-^—H1^ - искомые коэффициенты квадратуры. Здесь а”к - i-a коэф-
А „=0i=0z + 1
фициент и-го полинома в А-м фундаментальном сплайне. Данные формулы имеют 6-й порядок аппроксимации.
-
6. Двумерные квадратурные формулы б-го порядка для односвязных областей
На плоскости рассматривается область О с границей у, где у задана параметрически. В области рассматривается гладкая функция / (г,<р) . Поместим область в круг радиуса R и введём полярную сетку. Рассмотрим интеграл:
^f(r,
Представим подынтегральную функцию в виде разложения по фундаментальным 5-сплайнам 5-й степени:
f(r, X X yiJCi(<p)DJ(r) + O(h6) = S(r,<p) + O(h6). Подставив S(r, в искомый интеграл, получим квадратурные формулы: гг1 к2 ^S(r,^)rdrdg> = ^ ^суУу , где ciJ = ^C^DjWrdrdq). (3) Й '=о 7=0 Й Математика Для вычисления коэффициентов clJ воспользуемся формулой Грина в полярной системе координат: Q 1 дРг' Г dtp , г dr dtp. Для нашего случая положим Рг (г, ф) = 0, Q^ (г, tp) = —С t (tp) ^tD} (f)dt, тогда г о --(rQ )= С' (tp)D (г) и для квадратурных коэффициентов мы получаем формулы: г дг cij = ^С, (ф) ^tDj (f)dt dtp. г ч о > Точность приближения квадратурных формул для круга Кол-во полиномов Точность полученной формулы Коэфф-т улучшения 5 6,47x10-7 10 1,198х10-8 54,3 20 2,033x10"10 59 40 4,26x10’12 48 Точность приближения квадратурных формул для астроиды Кол-во полиномов Точность полученной формулы Коэфф-т улучшения 5 1,28 хЮ-2 10 2,69x10^ 47,5 20 4,77 x1g-6 56,4 40 1,03 хЮ-7 46,3 Рис. 1. Астроида Пусть выполнены условия устойчивости матрицы U, т.е. тх< М^*, т2< М2^ и пусть / g С6^^), где О^ ой, т.е. предполагается, что функция / непрерывна и шесть раз дифференцируема в несколько большей области. Пусть также h = тах(/г1,й2). Поместим область в круг К радиуса R. Введём полярную систему координат, взяв за начало координат центр круга К. Продолжим функцию / в K\QS тождественным нулём. Обозначим S(tp,r) - tp-r - сплайн, приближающий таким образом продолженную функцию / на круге К. Доказана следующая теор^арема 4. Пусть S(tp,r) - (р-г - сплайн, приближающий функцию f пусть (М-m)h< p(ys,у). Здесь р(у^,у) - расстояние между границами областей Ог и О соответственно. Тогда справедлива оценка: Xj-lX2-l Q <=0 у=0 Здесь ytj = /(ф,г) - значения функции/ в узлах сетки, весовые коэффициенты c'J определены формулой (4), суммирование производится лишь по тем индексам, для которых (ф^г^еС! s.
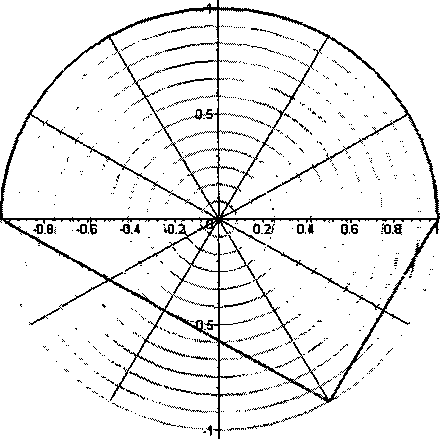
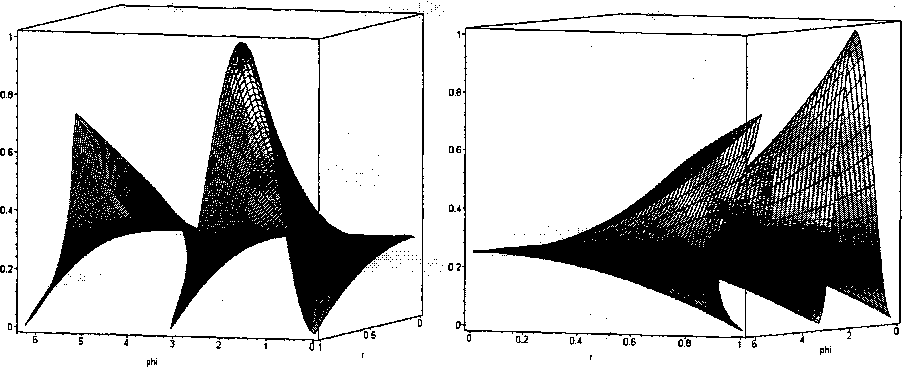
7. Решение задачи Дирихле для уравнения Пуассона в односвязной области Рассмотрим уравнение Пуассона в области D\ \ д ( ди г дЛ дг (r, С граничными условиями: u(r’^)\dD=^r’^’ где граница области D задана параметрически: Рис. 2. Область D, погруженная в круг радиуса 1 Уз sm(^>) + cos(^>) ’ Уз sin(^) - Уз cos(<^) ’ фе[0,л] фе[л,5л/3] Ф^ [5 л/3,2л-] Поместим D в круг радиуса 1. Далее, будем рассматривать полярную систему координат с центром в центре круга. Построим полярную сетку по г и по ^. Представим решение уравнения в виде: К\-\К2-\ <г,ф)=^ YufiW»D№> (7) г=0 у=1 где С,(ф) и Dj(f) - периодический и непериодический фундаментальные одномерные сплайны на отрезках [0,2л-] и [0, 1] соответственно. Домножим исходное уравнение на г. Теперь будем домножать полученное уравнение скалярно на Ci( д' D I д2и дг2 Ъ 1 о2 Т- + --J Cl (ф)Ок (г)Мф = - [^(r, (p)Ci ty)Dk {r')r2drdф. dr г дф D Подставим в левую часть выражение (7): Математика Zuu \\(c^D^ = - Wpkr^C^D^r^drdtp. D Здесь существенно, что выражения, стоящие под знаком интеграла в левой части является произведением функции от переменной г на функцию от переменной <р, поэтому, применяя формулу интегрирования по частям, можно избавиться от производных высоких порядков (например, при решении уравнения ^u(r, под знаком интеграла появятся производные 3-го и 4-го порядка от фундаментальных сплайнов, в то время как существует лишь непрерывная производная 2-го порядка, но интегрируя по частям, можно свести подынтегральное выражение к такому, в котором будут лишь производные 1 и 2 порядка). Последнее уравнение ввиду произвольности выбора Ink представляет собой систему для определения коэффициентов и^. Чтобы сделать систему полной, необходимо учесть граничные условия, которые дадут недостающее число уравнений: ^иуС^Щг) dD Интегралы в (8) вычисляются при помощи квадратурных формул для области D, коэффициенты которых находятся по формулам: Я f i c‘J = jc^tp) ^rDj(r)dr dtp + 5л/3 (r^fp) 2л ( гг(<Р) О <0 J Сф<р) | rDj(r)dr d(p+ j C^tp) J rDj(r)dr dtp, к О 5л!3 1 V3 где к фр) = —т=-------------, r2 (^) =--г------■ V3 sin(^) + cos(^) sin(^)-y3cos(^) Из системы уравнений (8) и (9) получаем коэффициенты и^ разложения решения (7) по фундаментальным сплайнам, т.е. искомое приближенное решение. Вышеописанным методом решалась задача: \ d ( 1 д2и , . . „ = (r,tp)eD Jr dr \ dr ) г dtp . М(Г>^)|Э£> =r2 sin2(^)-(r2 ~!)/4 При ^ = 12, ^2=6 точность решения составила 0,7927 x1g-4 . График решения представлен на рис. 3. Рис. 3. Решение уравнения Пуассона на области D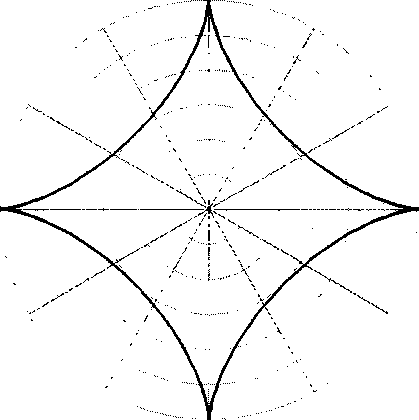
Список литературы Применение дважды непрерывно дифференцируемого S-сплайна
- Силаев, Д.А. Приближение S-сплайнами гладких функций/Д.А. Силаев, Г.И. Якушина//Труды семинара имени И.Г. Петровского. -М.: Изд-во МГУ, 1984. -Вып. 10. -С. 197-206.
- Силаев, Д.А. Дважды непрерывно дифференцируемые S-сплайны/Д.А. Силаев//Веста. Моск. ун-та, Сер. 1. Математика, механика. -2007. -№ 2. -С. 12-17.
- Силаев, Д.А. Решение краевых задач с помощью ^-сплайна/Д.А. Силаев, Д.О. Коротаев//Математика. Компьютер. Образование: сб. научн. трудов. Под ред. Г.Ю. Ризниченко. -М.Ижевск: НИЦ «Регулярная и хаотическая динамика», 2006. -Т. 2. -С. 85-104.
- Полулокальные сглаживающие сплайны класса С1/Д.А. Силаев, A.B. Амилющенко, А.И. Лукьянов, Д.О. Коротаев//Труды семинара имени И.Г. Петровского. -2007. -Вып. 26. -347-367.
- Semilocal smoothing spline of class С1/D.A. Silaev, A.V. Amiliyushenko, A.I. Luk'janov, O. Korotaev//Journal of Mathematical Sciences. -2007. -V. 143, № 4. -P. 3401-3414.
- Силаев, Д.А. О квадратурных формулах высокого порядка аппроксимации для произвольных областей/Д.А. Силаев//Современная математика и математическое образование, проблемы истории и философии математики: Международная научная конференция, Тамбов, 22-25 апреля 2008 г./отв. ред. A.A. Артёмов. -Тамбов: Изд-во Першина Р.В., 2008. -С. 65-70.


