Применение фрактальной геометрии в исследовании речных систем

Новикова Т. C., Булякова И. А. Применение фрактальной геометрии в исследовании речных систем // Системный анализ в науке и образовании: сетевое научное издание. 2024. № 2. С. 9-20. EDN: DNZNAK. URL :

Novikova T. S., Bulyakova I. A. Application of fractal geometry in the study of river systems. System analysis in science and education, 2024;(2):9-20 (in Russ). EDN: DNZNAK. Available from:

Статья находится в открытом доступе и распространяется в соответствии с лицензией Creative Commons «Attribution» («Атрибуция») 4.0 Всемирная (CC BY 4.0)

С давних времен человечество изучало лишь идеальные фигуры: окружности, параллелограммы, треугольники, которых нет в реальном мире, но которые относительно просто описываются. Знакомая всем школьная геометрия не способна описать облака, потому что это не просто сферы, горы, которые лишь очень приближенно похожи на конусы, а о причудливых формах береговой линии и вообще говорить не приходится, тут уж и представить нельзя, чем их можно аппроксимировать. Окружающий нас мир гораздо сложнее, не все можно заменить на что-то просто устроенное. Существует множество вещей, обладающих замысловатыми формами и свойствами, описывать которые нужно соответствующими объектами. И тут нам помогут фракталы.

Открытие фракталов произвело революцию не только в геометрии, но и в физике, химии, биологии, во всех областях нашей жизни. Фракталами в живой природе являются кораллы, цветы и другие растения (брокколи, капуста Романеско), плоды (ананас), кровеносная система и бронхи животных. Много их и в неживой природе. Например, уже упомянутые береговые линии, горные хребты, и облака, а также снежинки, молнии и кристаллы. Даже человек, если задуматься, является в некотором роде фракталом. Он рождается ребенком, а затем растет, и этот процесс сопровождается «принципом самоподобия», фрактальностью.

Фракталы широко применяются в компьютерной графике при построении изображений деревьев, кустов, гор и других природных объектов. Из фракталов делают антенны, точнее используют лишь несколько первых их итераций. Удобство таких антенн заключается в их дробной размерности. Фракталы даже используют в торговле, так как они лучше описывают поведение рынка, чем линейные функции. [1-5]

Таким образом, фракталы можно встретить почти везде. Они замечательно описывают многие природные объекты, в том числе и речные системы, речь о которых пойдет в этой работе.

Фрактал и фрактальная размерность

Начнем погружение в мир фрактальной геометрии с основного ее понятия – фрактальной размерности. И первое слово в этом понятии – фрактал. Фрактал – это фигура, у которой хаусдорфова размерность превышает топологическую размерность. Топологическая размерность – это привычная всем геометрическая размерность. Она может принимать только целые значения. Так, для отрезка она равна 1, для квадрата 2, а для куба – 3.

Теперь разберемся с хаусдорфовой (фрактальной) размерностью. Если обратиться к топологической размерности, то для единичного отрезка, если мы меряем его отрезком длинной r = 1/3, то его длину можно найти как:

N*r = 1

Площадь единичного квадрата при измерении маленькими квадратиками со стороной r = 1/3 равна:

N * r2 = 1

А для объема единичного куба, измеренного кубами со стороной r = 1/3, получим формулу для объема (см. рис. 1):

N * r3 = 1

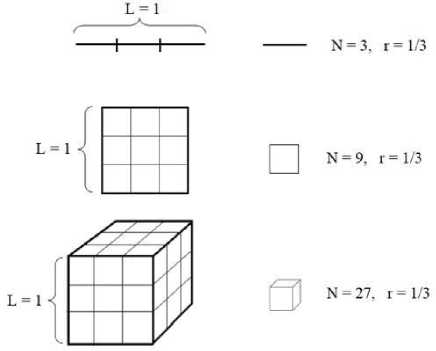
Рис. 1. Вывод формулы фрактальной размерности

Получается, что размерность совпадает со степенью r, а значит можно записать в общем виде:

N * rD = 1

Выразим D из этой формулы:

log(N • rD) = log 1 log N + D • \ogr = 0

D • log r = -log N

—D • log(-) = -log N r

D^

logr

Например, в случае измерения отрезками, это означает, что при уменьшении длины отрезка, отношение логарифма количества потребовавшихся для измерения отрезков к логарифму длины отрезка будет в пределе давать фрактальную размерность. [6, 7]

Алгоритмы измерения фрактальной размерности

Теперь, когда мы разобрались с тем, что такое фрактальная размерность, необходимо понять, как ее можно посчитать. Рассмотрим несколько алгоритмов, позволяющих это сделать.

Клеточный метод (box-counting dimension)

• -    Линия покрывается сеткой с размером ячейки 3.

• -    Подсчитывается количество клеток N(3) , накрывающих исследуемую линию.

• -    Далее величина 3 несколько раз уменьшается и два предыдущих пункта повторяются (см. рис. 2).

• -    В результате этого получаем несколько пар значений 3 и N(3) , для которых вычисляем логарифмы. Далее строим систему координат в двойном логарифмическом масштабе и наносим точки с полученными координатами на плоскость. Проводим прямую линию через эти точки (см. рис. 3).

  

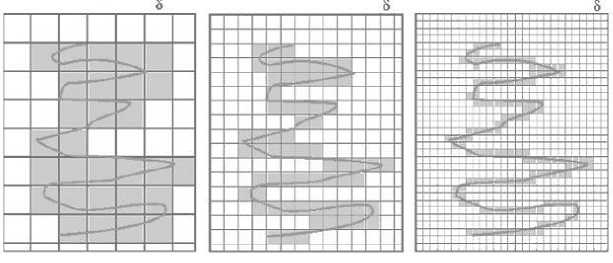
  Рис. 2. Клеточный метод

  
  
  

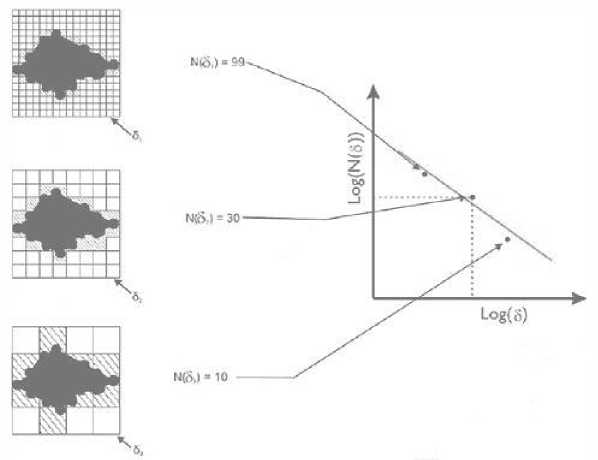
  Рис. 3. Полученные точки в билогарифмическом масштабе

  
  

  - Далее определим угол наклона линии регрессии (см. рис. 4).

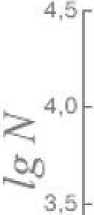
D~ 1,52 ±0,01

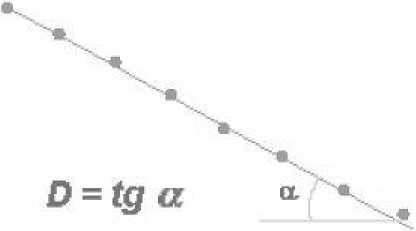
3,01________________i_________________।_________________!_________________[________________r -0,5     0      0,5      1.0      1,5      2.0

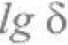
Рис. 4. Определение угла наклона линии регрессии

• -    Клеточная фрактальная размерность D будет равна тангенсу этого угла.

Канторовский метод (квадраты)

• -    Изображение покрывается сеткой, состоящей из квадратов, с площадью ε² каждый.

• -    Подсчитывается число пересечений N(s) линии на изображении с клеткой сетки.

• -    Повторяются два предыдущих шага с увеличением количества задействованных клеток сетки на одну (см. рис. 5).

• -    Строится график зависимости N(e) в билогарифмических координатах. Методом наименьших квадратов оценивается наклон этого графика, он и представляет собой размерность блуждания h, через которую по формуле находится фрактальная размерность:

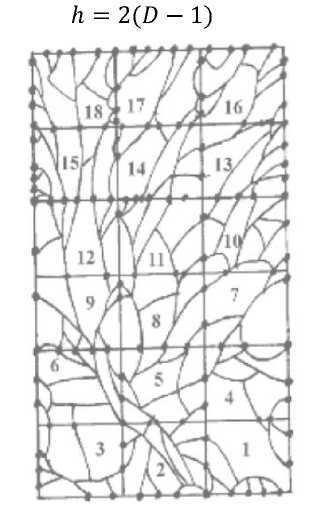
h = 2(D- 1)

Рис. 5. Квадратная сетка для канторовского метода

Канторовский метод (окружности)

• -    Выбирается раствор циркуля г - радиус окружности.

• -    Строится окружность и подсчитывается число пересечений N(e) линии на изображении с этой окружностью.

• -    Повторяются два предыдущих шага с увеличением раствора циркуля г от минимального до максимального, центр окружности при этом не меняется (см. рис. 6).

• -    Строится график зависимости N(s) в билогарифмических координатах. Методом наименьших квадратов оценивается наклон этого графика, он и представляет собой размерность блуждания h, через которую по формуле находится фрактальная размерность D :

h = 2(D- 1)D=h+1

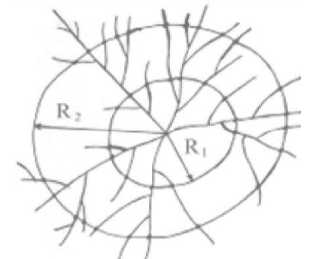
Рис. 6. Сетка из кругов для канторовского метода

Результат можно обосновать следующим образом. Если ветвлений нет, то число N не зависит от размера R , т.е. в этом случае D = 1, N = const и h = 0.

Если ветвления полностью заполняют плоскость, то их число N прямо пропорционально площади области, т.е. в этом случае D = 1, N = R * R и h = 2 (см. рис. 7) [6, 7].

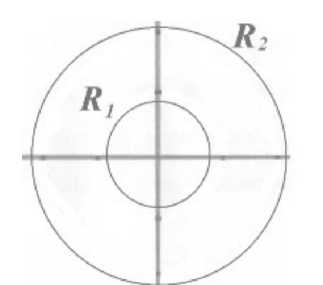
Рис. 7. Обоснование формулы

Применение методов в гидрологии

Описанных методы можно использовать в гидрологии. Более 70% земного шары покрывает вода и лишь около 30% занимает суша. Поэтому важно изучать гидросферу нашей планеты. Но все оказывается не так уж и просто. Так, при измерении длины береговой линии Великобритании люди получали совершенно разные результаты. И все из-за того, что они использовали разные масштабы. Кто-то смотрел, сколько отрезков по 100 метров укладывается в очертания береговой линии, а кто-то в качестве единицы измерения брал 10 м и получал значительно большую длину. Но кто же ошибался? Как оказалось оба были правы. Измерим длину береговой линии, заменяя ее ломаной линией, составленной из отрезков длины г.

Если г ^ 0, то мы учитываем все больше и больше изгибов берега, а значит длина стремится к бесконечности. Тогда длина береговой линии Британии была бы бесконечной если бы мы измеряли ее отрезками, длина которых стремится к нулю (см. рис. 8).

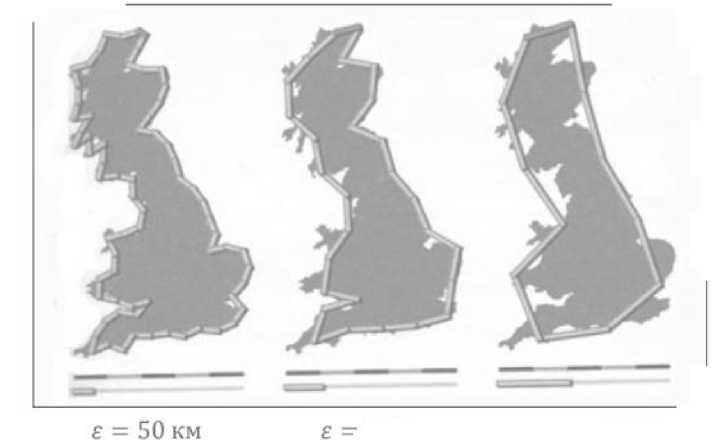
£ = 100 км

£ = 200 км

Рис. 8. Иллюстрация подсчета длины береговой линии

Поэтому лучше определять береговую линию степенью ее изгибания (а не длиной), которую Б. Мандельброт и предложил назвать фрактальной размерностью.

Так же и с речными системами – в зависимости от выбранного масштаба можно получить совершенно разные значения протяженности речной системы. А определение фрактальной размерности дает вполне конкретный результат, в связи с чем фрактальная геометрия является хорошим инструментом для описания рек.

Выполненные расчеты

Расчеты для дельты Волги

Рассмотрим применение описанных методов для дельты реки Волги. Расчеты будем проводить по следующему изображению 500*500 пикселей (см. рис. 9), источник:

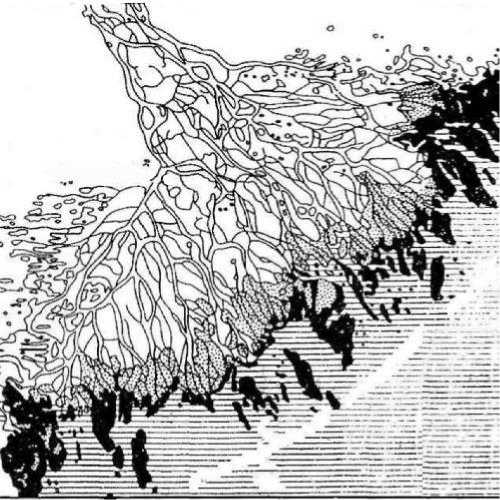
Рис. 9. Дельта Волги

Для клеточного метода необходимо задать параметры сетки, накладываемой на изображение. И в случае цветного изображения применить фильтр, для преобразования в черно-белое. Разобьем сначала на 10 частей по горизонтали и вертикали (т. е получим, что каждая клетка имеет размер 500/10=50 пикселей) и далее будем постепенно увеличивать количество клеток вплоть до разбиения на 100 частей. И по результатам подсчета количества занятых (черных клеток), использую линейную регрессию (см. рис. 10), получим следующее значение фрактальной размерности: D 1 = 1.61

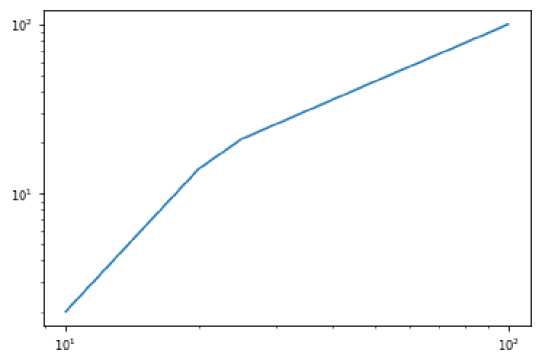
Рис. 10. График в билогарифмическом масштабе для клеточного метода

Далее получим фрактальную размерность канторовским методом, путем определения количества пересечений изображения с квадратной сеткой, начиная от верхнего левого края. В данном методе будем использовать часть изображения, так как он чувствителен к пропускам данных (белые промежутки, где нет реки на исходном изображении) (см. рис. 11).

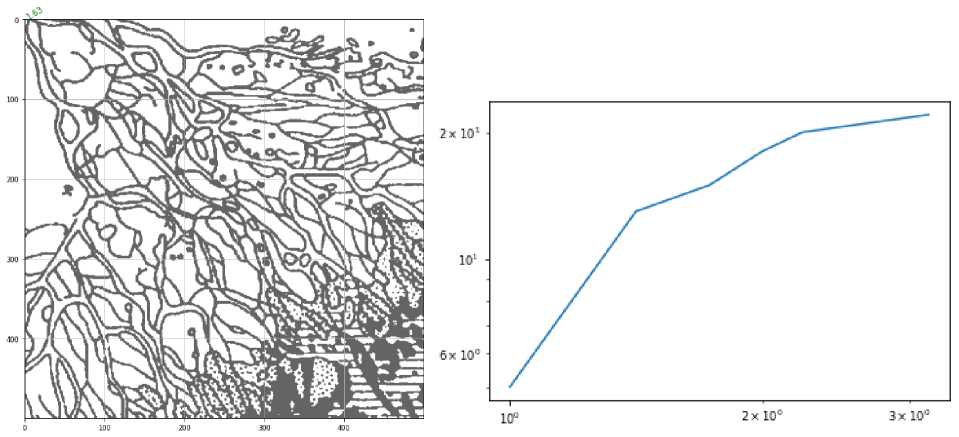
Рис. 11. Работа канторовского метода с наложение квадратной сетки

Применяя описанный ранее алгоритм получим: D 2 = 1.63.

И в последнем канторовском методе с окружностями задаем центр всех окружностей в точке (100, 0) и постепенно увеличиваем радиус окружности с центром в этой точке с шагом в 30 пикселей. При этом учитываем не всю окружность, а ее четверть от 270 до 360 градусов ввиду геометрии дельты (см. рис. 12).

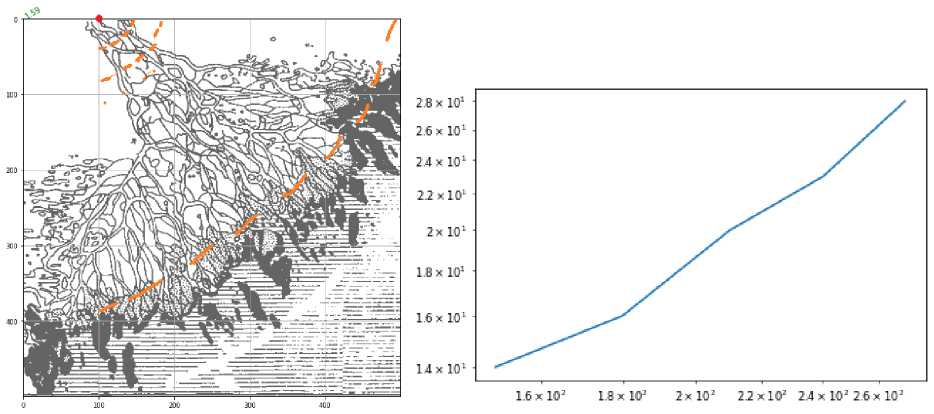
Рис. 12. Работа канторовского метода с окружностями

Расчеты данным методом показывают значение: D 3 = 1.59.

Таким образом, три метода дали следующие результаты (табл. 1) :

Табл. 1. Фрактальная размерность дельты Волги

Метод	Клеточный	Канторовский(квадраты)	Канторовский(круги)
Значение   фракталь ной размерности	1.61	1.63	1.59

В данном примере все три метода показали схожие результаты, что подтверждает правильность расчетов. Но при этом мы имели неплохое качество изображения и четкий, схематичный рисунок дельты, где каждый приток изображен тонкой линией. Далее рассмотрим менее схематичное изображение.

Расчет для участка Волги в месте слияния с Камой

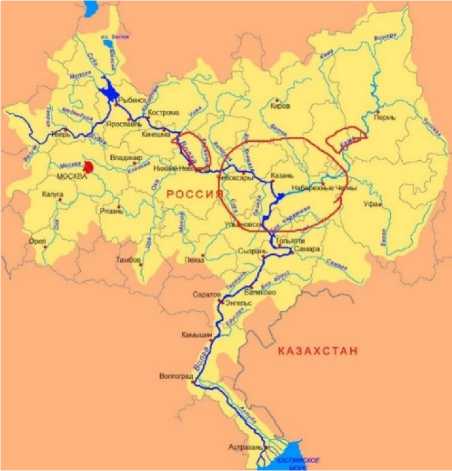
Рис. 13. Слияние Волги с Камой

Для расчетов будем использовать часть следующего изображения (см. рис. 14), источник:

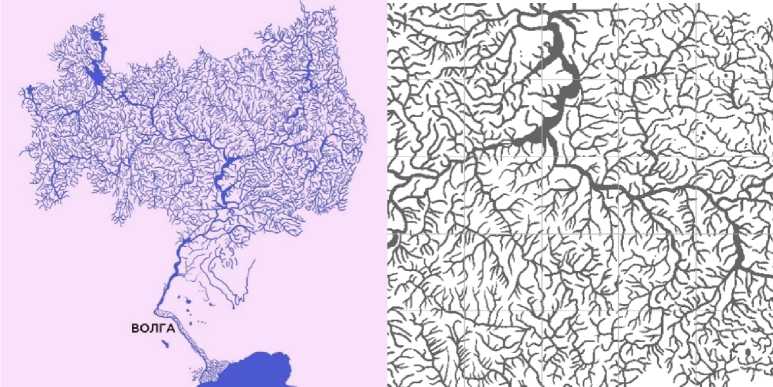
Рис. 14. Изображение для применения алгоритмов

Табл. 2. Фрактальная размерность участка впадения Камы в Волгу

Метод	Клеточный	Канторовский(квадраты)	Канторовский(круги)
Значение фрактальной размерности	1.93	1.70	1.66

В данном случае разброс в значениях (табл. 2) более существенный и связанно это с особенностями методов. Применяемый нами канторовский метод измерения обладает существенной эффективностью по сравнению с другими методами. Если использовать клеточный метод, то размер клетки должен быть заметно больше толщины русла реки, при этом используемая карта дельты реки должна быть подробной, учитывать все извилины рукавов и протоков. Канторовский метод позволяет использовать схемы ветвлений с меньшей детализацией условных границ дельты.

Сравнивая пример 1 и 2 можно сделать вывод (по значению фрактальной размерности) о большей густоте участка речной системы в месте пересечения Волги с Камой (фрактальная размерность 1.747), нежели дельты Волги (фрактальная размерность 1.610). Это также можно подтвердить и визуально (см. рис. 15).

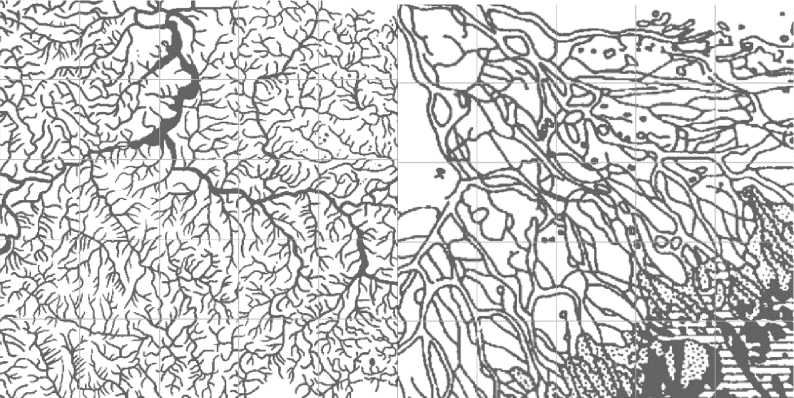
Рис. 15. Волга и Кама/Дельта Волги

Сравнение фрактальной размерности участков Волги

Мы сравнили фрактальные размерности двух участков реки Волга. Также можно накладывать сетку на изображение и исследовать конкретные участки речных систем или даже всю речную систему, например, для определения водонасыщенности территории (чем больше фрактальная размерность, тем больше водонасыщенность) и, как следствие, предотвращения последствий полноводья или же для определения места постройки технических сооружений (см. рис. 16). На рисунке красным цветом отмечены наиболее подверженные затоплению участки, а зеленым – сегменты, где волноваться не о чем.

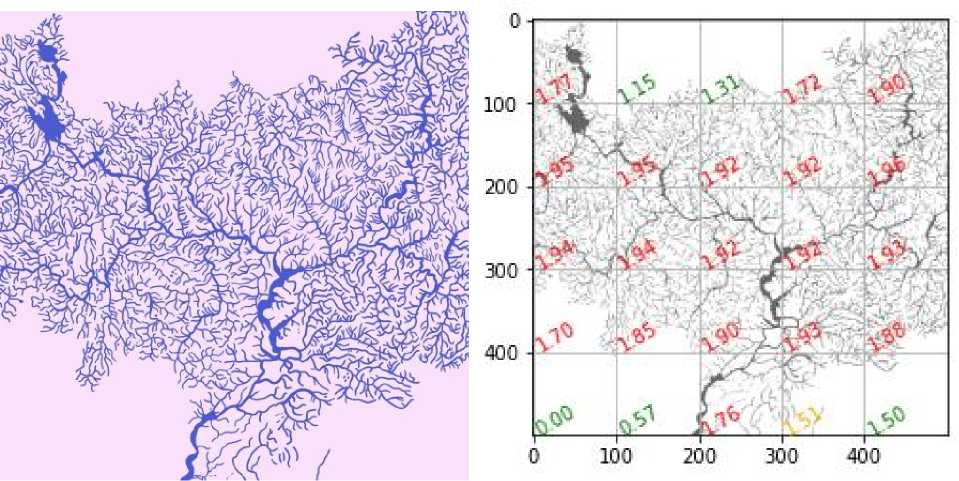
Рис. 16. Сравнение участков Волги

Расчеты длины береговой линии Рыбинского водохранилища

Рассмотрим еще один пример использования фрактальной размерности в гидрологии. Это определение длины береговой линии рыбинского водохранилища (см. рис. 17, 18, табл. 3), источник исходного изображения:

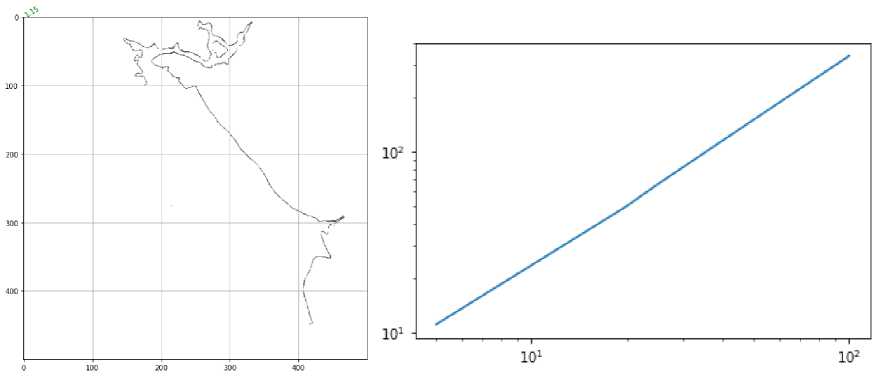
Рис. 17. Фрактальная размерность правой части береговой линии рыбинского водохранилища

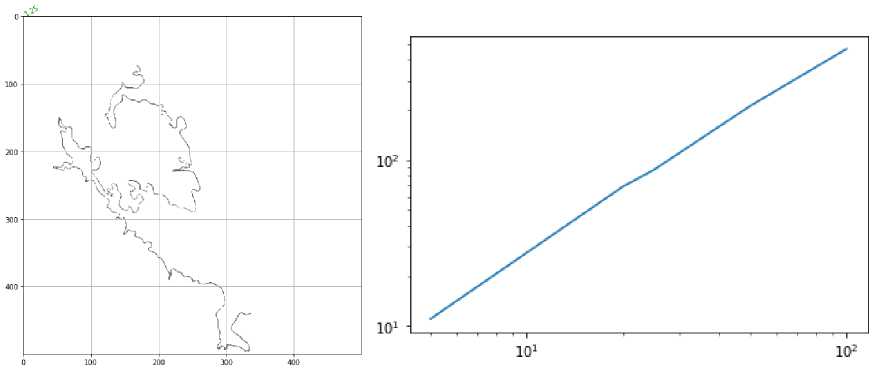
Рис. 18. Фрактальная размерность левой части береговой линии рыбинского водохранилища

Табл. 3. Фрактальная размерность рыбинского водохранилища

	Левая часть берега	Правая часть берега
Фрактальная размерность	1.25	1.15

Пример иллюстрирует различие в правой и левой части береговой линии. Исходя из полученных значений можно сделать вывод о большей извилистости левой части по сравнению с правой.

Заключение

В работе рассмотрены основные понятия фрактальной геометрии, показаны способы ее использования в гидрологии. Сведения о фрактальных параметрах рек имеют большое значение и пригодятся в схемах комплексного использования и охраны водных объектов, информационных системах и базах данных о водных объектах, для развития методов гидрологических расчетов и прогнозов при управлении водными ресурсами.

Рассматривая водные ресурсы, можно найти множество вариантов применения фрактальной геометрии. Но схожие паттерны наблюдаются и в исследовании грозовых разрядов, овражно- балочных сетей, кластеров в химии и многих других объектов. Поэтому фрактальная геометрия имеет большое практическое применение и важна для изучения.