Применение функции взаимной корреляции для картирования сдвигов по данным потенциальных полей (на примере трансформных разломов хребта Колбейнси)

Крупные сдвиговые системы мира располагаются в областях с различными геодина-мическими режимами, а также с тяготением к подвижным областям литосферы. В научной литературе отображены глобальные сдвиговые системы и их связь с современной тектонической активностью (Jiannan et al., 2023), а также роль в контроле размещения металлических полезных ископаемых (Карамышев и др., 2020; Шахтыров, 1997) и углеводородов (Тимурзиев, 2013), в связи с чем такие объекты интенсивно изучаются методами геологии, геофизики, геомеханики. Среди хорошо изученных мировых сдвиговых систем можно перечислить знаменитый разлом Сан-Андреас, Анатолийские Северный и Восточный разломы, Денали, Куньлунь, Пияианг (Адамович др., 1991). Распространение сдвиговых систем мира иллюстрируется обзорной схемой (рис. 1), со- ставленной по литературным материалам с использованием различных тектонических карт (Адамович и др., 1991; Mann, 2007; Molnar, Dayem, 2010) и подложки в виде Тектонической Карты Мира (TeMaW). В пределах российских территорий выделяют ряд сдвиговых систем с меньшей проявленностью и в целом меньшей изученностью – Байкало-Становую сдвиговую зону (Ageev et. al., 2020; Егоров, Агеев, 2023), Чукотский сдвиг, ряд сдвигов Верхояно-Колымской складчатой области (Карамышев и др., 2020), разлом сдвигового характера в основании Енисей-Хатангского прогиба (Афанасенков и др., 2018), сдвиги в основании ЗападноСибирской плиты (Иванов, 2005) и др.

Отдельным классом среди разломов с латеральным смещением схожих блоков земной коры относительно друг друга являются трансформные разломы характера «хребет-хребет», которые наиболее широко распространены в пределах акваторий океанов и

имеют специфическую транстенсионную кинематику. Понятие трансформных разломов впервые было предложено Д. Уилсоном (1965 г.). Это разломы, по которым смещение блоков пород внезапно прекращается или изменяет характер и направление и трансформируется в другой тип геологических структур. Как следует из определения, не все трансформные разломы могут быть ассоциированы со сдвигами. И даже те трансформы, которые приводят к смещению осей спрединга, физически характеризуются иным процессом формирования дизъюнкти-ва – они не рассекают сформированный хребет на отдельные сегменты, как это характерно для чистых сдвигов, а «растут» одновременно с развитием хребта. Трансформные разломы в окрестностях дивергентных границ формируются из-за того, что скорость спрединга различных сегментов литосферы отличается, что может быть вызвано разными факторами: неравномерным тепловым потоком, разными размерами магматического очага, объемом и скоростью вулканизма, физическими характеристиками коры и т.д. Компенсация этих разностей достигается «растрескиванием» литосферы и смещением по сети поперечных разломов. Однако результат развития деформаций – образ латерального смещения блоков пород – схож с чистым сдвигом, поэтому такие трансформы поддаются интерпретации наравне с классическими сдвигами, в том числе предлагаемым в работе способом.

В целом на обобщенной схеме (рис. 1) отражены структуры, которые характеризуются значительной длиной и преобладанием горизонтального смещения в кинематике со значительной амплитудой смещения, также отмечены центральные части «сдвигов Уилсона».

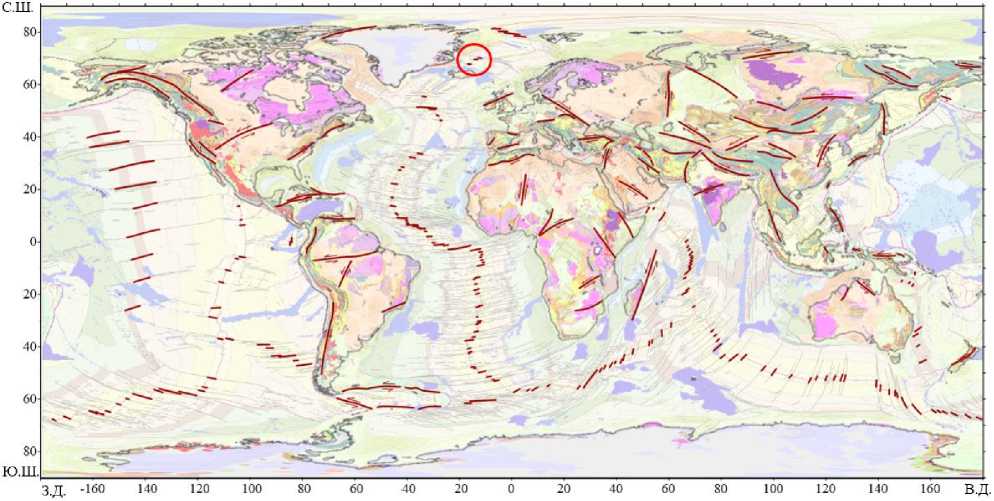
Рис. 1. Генерализованная схема региональных сдвиговых и трансформных структур мира. Красным кругом отмечена зона более детального рассмотрения. В качестве подложки использована Тектоническая Карта Мира (TeMaW)

Дизъюнктивы длиной более 1000 км принадлежат к наиболее крупным и глубинным разрывным нарушениям планеты, а большинство из них, будучи приуроченными к границам литосферных плит, вероятно, проникают до кровли астеносферы как в океанах, так и на континентах. Энергетическим источником сдвиговых систем литосферы считаются эндогенные процессы под лито- сферой и частично в ней, которые индуцируют сдвиговые поля напряжений, вызывающие деформации глобального масштаба (Шерман и др., 1991).

В отличие от разрывных нарушений с вертикальным смещением, которые могут быть ограничены небольшой площадью, при латеральных сдвигах смещение одного блока земной коры обязательно вызывает смеще- ние или деформацию примыкающего, что способствует большей протяженности таких дислокаций.

Зачастую сдвиговые зоны сопровождаются заложением характерных деформаций и соответствующих геологических особенностей: структур цветка, конского хвоста, сколов Риделя и др. (Фролова и др., 2019). Эти дислокации, сопровождающие сдвиговые нарушения, позволяют надежно их картировать и определять кинематику даже при проведении исследований среднего и малого масштабов. Например, широко известный сдвиг – разлом Сан-Андреас – имеет протяженность около 1280 км, формируя при своем развитии цепочку оперяющих второстепенных дислокаций, также со сдвиговой составляющей в кинематике. Необходимо отметить, что сдвиги ранних стадий развития представляют собой широкие зоны повышенной концентрации сравнительно коротких разрывных нарушений в земной коре, располагающихся кулисообразно под острым углом к простиранию оси сдвига (Фролова и др., 2019). В отличие от них, сдвиговые зоны поздних стадий формирования являются протяженными разломами с большими амплитудами горизонтальных перемещений, которые в местах сочленения кулисообразных разрывов друг с другом образуют широкие участки повышенной раздробленности. Проявленность сдвиговых структур разных этапов формирования в геофизических данных будет отличаться, также будет различным их влияние на рудо-образование и формирование ловушек углеводородов.

Геофизическая проявленность сдвиговых систем

Качественное сопоставление взаимосвязей геолого-геофизических процессов с морфолого-генетическими группами разломов выдвинуло из них сдвиги как разновидность разрывов, которым присуща тесная корреляция с наиболее широким комплексом геолого-геофизических явлений (Шерман и др., 1991). При этом интерпретация таких деформаций бывает затруднена вплоть до того, что по одним и тем же картам потенциаль- ных геофизических полей (на участках затрудненных прямых геологических наблюдений) разными исследователями могут быть выделены сдвиги различных простираний, что, согласно опыту участия авторов в научных мероприятиях, порождает множество дискуссий. Достаточно однозначно проявляются сдвиговые зоны в данных 3D-сейсморазведки, где их основной образ связан с кулисообразными нарушениями в плане и «цветковыми структурами» в разрезе (рис. 2а). Пример развитого сдвига, проявленного в данных потенциальных полей (на примере схемы аномального магнитного поля), показан на рис. 2б – здесь надежно угадывается прерывание осей аномалий и их смещение.

При картировании разрывных нарушений различных типов активно используются данные потенциальных полей в площадном представлении – гравиразведки и магниторазведки, как собственно поля, так и их трансформации (Долгаль, 2022). Показательным математическим преобразованием поля при этом считается модуль горизонтального градиента, позволяющий выделять границы крупных блоков пород с контрастными свойствами, зачастую имеющих тектоническую природу. Существует также ряд усовершенствованных трансформаций, или способов автоматического линеаментного анализа, пригодных для трассирования разломов по площади исследования (Бедненко, 2003; Luan et al., 2022). Указанные способы хорошо картируют сбросы, взбросы, разломные зоны с интенсивными вторичными преобразованиями (Керимов и др., 2012). Однако сдвиговые зоны идентифицируются обычно по комплексу косвенных признаков, а напрямую наличие смещения в аномалиях, как в разорванных геологических комплексах, часто игнорируется.

Целью настоящей работы является обсуждение трансформаций потенциальных полей и создание такой трансформанты, которая бы позволила определять автоматически зону сдвига и величину смещения блоков пород вдоль этой зоны для сдвиговых нарушений поздних стадий формирования.

а

б

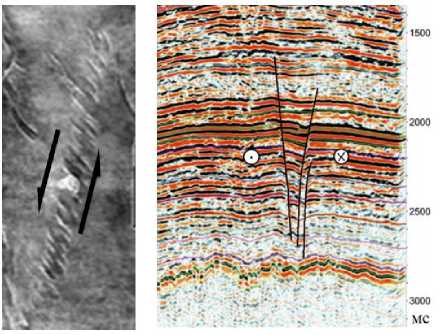
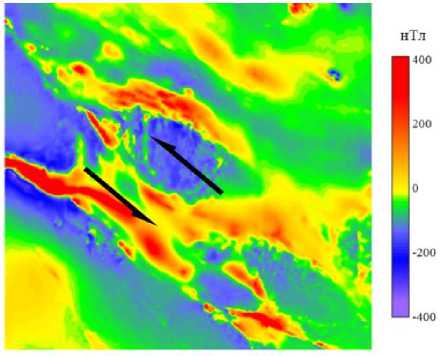
Рис. 2 . Примеры геофизической проявленности сдвиговых систем: а – в данных 3D-сейсморазведки на структурной карте и в разрезе (Западная Сибирь), б – в данных магнитного поля (Восточная Сибирь)

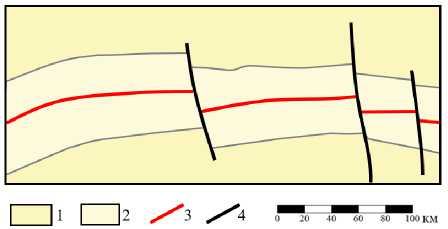
Рис. 3. Фрагмент тектонической карты (TeMaW) участка исследования, 1 – океаническая кора миоценового возраста, 2 – океаническая кора плиоценового возраста– голоцена, 3 – дивергентные границы, 4 – прочие разрывные нарушения (трансформные)

Особенности геологического строения и магнитное поле окрестностей хребта Колбейнси

В качестве показательного примера рассмотрим район, расположенный к северу от Исландии в Северном Ледовитом океане, – хребет Колбейнси, являющийся сегментом Срединно-Атлантического хребта. Развитие тектонических процессов в данном регионе представляется довольно сложным с момента начала спрединга в позднем палеоцене – начале эоцена (Brandsdóttir et al., 2015). Аномалии магнитного поля здесь фрагментарно разорваны, имеют локально непараллельное простирание и форму, отражающую перескоки оси спрединга и наличие зон аккреции коры. Значительный по размерам перескок оси спрединга связан с замершим в настоящее время рифтогенезом хребта Эгир (Greenhalgh, Kusznir, 2007) и активизацией хребта Колбейнси, которые расположены практически параллельно друг другу на расстоянии около 500 км.

В окрестностях хребта имеются трансформные разломы, располагающиеся субперпендикулярно к дивергентным глубинным разломам, которые формируются в ходе спрединга (рис. 3).

На рисунке 4а изображена схема аномального магнитного поля, извлеченная из модели WMM (World Magnetic Model, 2020) для участка детального рассмотрения, а также некоторые трансформации, которые часто применяются для анализа тектонической обстановки. Представлены модуль горизонтального градиента магнитного поля (рис. 4б), результат автоматического трассирования линеаментов по макросу Lineaments (по М.Б. Штокаленко) (рис. 4в), карта угла наклона градиента поля (tilt derivative – TDR) (рис. 4г). На данных рисунках отмечается ось спрединга и система субпараллельных более ранних структур. Видно, что ось спре-динга претерпевает разрывы, которые корре- лируют с закартированными трансформными разломами. При этом ни одна из трансформаций не выделяет зоны «сдвига» как целевые – повышенными или пониженными значениями соответствующего условного параметра. Таким образом, зоны разломов здесь можно выделить по нарушению корреляции осей аномалий и трансформант, в данном случае довольно явному, без привлечения дополнительной информации. В практике реальных геологоразведочных работ это выполняется крайне редко.

б

а

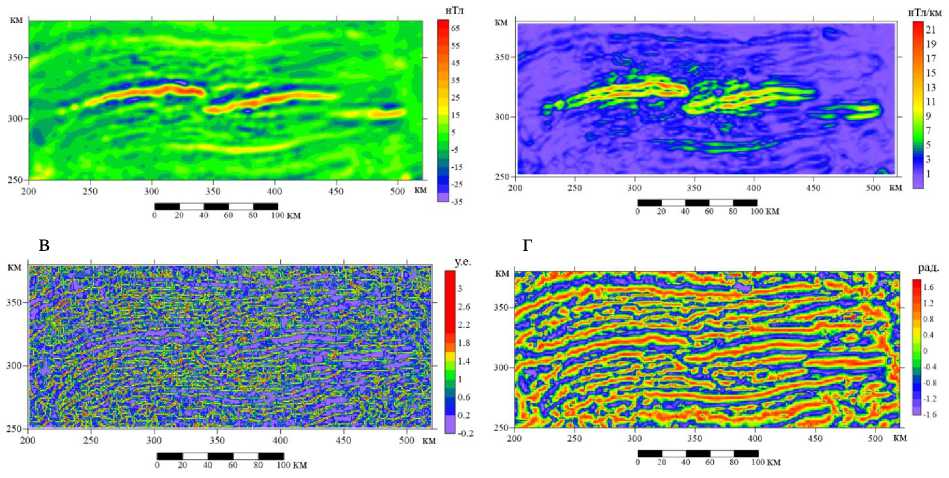
Рис. 4. Магнитное поле изучаемого региона (а) и примеры трансформаций, часто применяемых при трассировании разрывных нарушений: б – модуль горизонтального градиента, в – результат трассирования линеаментов по макросу Lineaments (по М.Б. Штокаленко), г – угол наклона градиента (tilt derivative – TDR). Система координат локальная

Классический анализ синтезированного поля со сдвигом

Подчеркнуть этот недостаток классических трансформант можно, анализируя синтезированную схему распределения аномалий, показанную на рис. 5а. Здесь представлено поле, которое можно воспринимать как условное площадное распределение магнитных или гравитационных аномалий. Видно наличие вытянутой субширотной пары положительной и отрицательной аномалий с разрывами, которые могут интерпретироваться как левосторонний сдвиг на координате х = 5 км и правосторонний – на координате х = 13 км. Поле осложнено малоамплитудным случайным шумом. Трансформации, аналогичные представленным на рис. 4б-г, показывают также, что синтезированные авторами сдвиговые зоны проявляются только по косвенным признакам – разрывам осей аномалий.

Функция взаимной корреляции (ФВК) как способ оценки смещений при анализе сдвиговых деформаций

На основе примеров (рис. 4, 5) мы видим, что классические трансформации, применяемые при трассировании разрывных нарушений, не позволяют явно выделить зоны сдвига как целевые объекты. Способом выделения таких областей, по мнению авторов, может служить расчёт функции взаимной корреляции (ФВК) в параллельных скользящих по-профильно окнах. В целом идея применения различных корреляционных характеристик в геофизике имеет давнюю историю (Kvamme, 2018), в том числе функция взаимной корреляции в разных вариантах может быть рассчитана в программах «КО-СКАД 3Д», «ГИС ИНТЕГРО» (Комплекс спектрально-корреляционного анализа данных…, Геоинформационные технологии для природопользования…). Авторы предлагают новый подход: выполнять построение карты положения максимума ФВК, которое будет

а

б

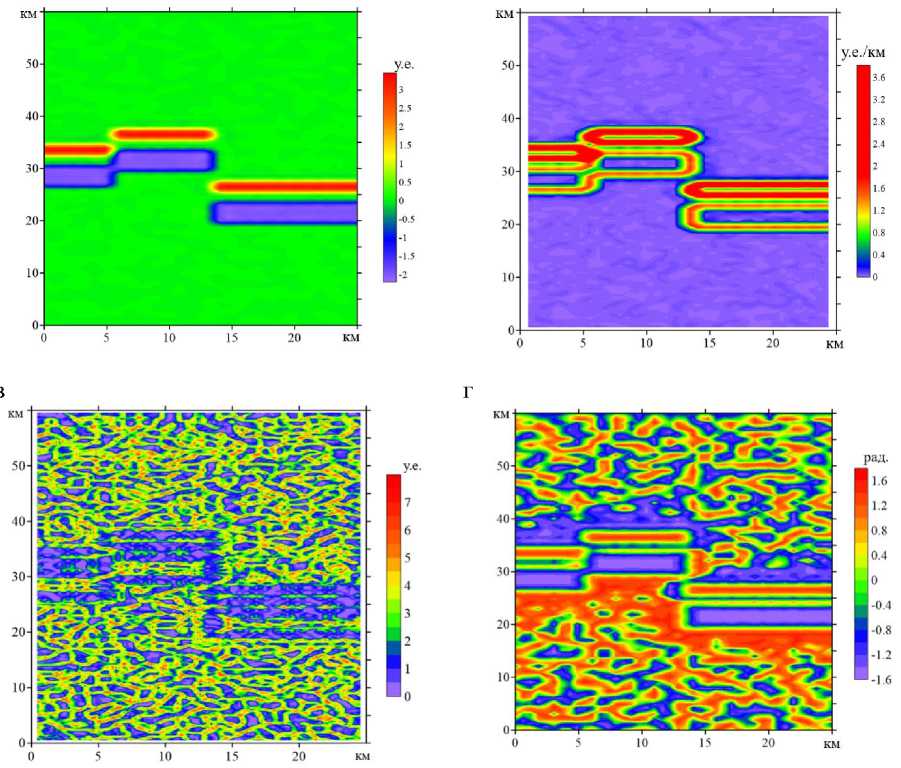
Рис. 5. Модельное (синтезированное) поле (а) и примеры трансформаций, часто применяемых при трассировании разрывных нарушений: б – модуль горизонтального градиента, в – результат трассирования линеаментов по макросу Lineaments (по М.Б. Штокаленко), г – угол наклона градиента (tilt derivative – TDR)

соответствовать амплитуде смещения по сдвигу с указанием на лево- или правосторонний сдвиг в знаке полученной трансформации (рис. 6) и будет, таким образом, прямым признаком сдвигового нарушения в геофизических данных.

Для реализации данной идеи был разработан пакет макросов WindowXCorr (автор А.Е. Асосков), выполняющий расчёт статистических корреляционных параметров в парных скользящих окнах, перемещающихся по всему планшету исходных данных от профиля к профилю. Программа в настоящий момент разрабатывается, опробуются различные способы расчета, тем не менее текущие результаты позволяют рассмотреть способ как полезный инструмент для интерпретации и продемонстрировать начальные наработки.

Формула, применяемая для расчёта функции взаимной корреляции в текущей реализации алгоритма, имеет следующий вид:

i =+x

В (т )=Z U,- V-т, i=—^

где

U = { u^ ..-u 2 ,u 1 , u 0 , u 1 ,u 2 ...1I , }

V = {v—«... v—2, v—1, v0, v1, v2-..v+»}

– ис-

ходные сигналы, то есть выборки по параллельным профилям, ограниченные размера- ми скользящего окна;

В ( т )

– взаимнокорре-

ляционная функция – функция, зависящая от параметра смещения т ; Ui - i-ый отсчёт сигнала U; Vi - i-ый отсчёт сигнала V; т - вели- чина смещения.

В качестве сигналов U и V используются данные по двум параллельным профилям цифровой модели поля, равные по длине задаваемому размеру скользящего окна и находящиеся по разные стороны от точки расчёта. Для каждой точки поля, за исключением краевых, расчёт выполняется при различных смещениях сигналов U и V, при этом определяются два параметра: максимум взаимно-корреляционной функции и смещение, при котором наблюдается этот максимум, иными словами, рассчитывается положение максимума ФВК. В результате формируются две выходные сети данных, первая из которых характеризует величину смещения по разрывному нарушению (что интерпретируется как амплитуда сдвига), а вторая – величину максимума ФВК (этот результат несет вспомогательную функцию для оценки достоверности определения амплитуды сдвига). Полученные карты удобно использовать для выделения зон сдвига и отбраковки расчетных аномалий, по сравнению с другими способами представления информации о ФВК, предлагаемой в существующих программных комплексах. В настоящей работе представлены результаты расчета только первого из параметров (наиболее показательного) – положения максимума ФВК (рис. 7, 8).

При запуске программы интерпретатором задаются параметры скользящего окна, выбранные исходя из масштабов изучаемых объектов, предполагаемой величины и кинематики их смещения и детальности ис- ходных данных. При этом точкой отнесения расчёта функции взаимной корреляции является центральная точка между профилями, где заданы парные скользящие окна. В целом, как показал опыт авторов на модельных примерах (Asoskov, Matykina, 2023), достаточно близкие результаты могут быть получены при расчёте абсолютной, нормированной функции взаимной корреляции или скользящего коэффициента линейной корреляции между данными в параллельно смещающихся окнах.

Для демонстрации результативности алгоритма расчёт по предложенной методике выполнен для синтезированной модели, показанной на рис. 5а. Результат (рис. 7а, б) с высокой уверенностью способствует выделению двух зон сдвига: левосторонний с амплитудой смещения около 4 км на координате х = 5 км и правосторонний (на что указывает знак минус в параметре, отраженном на карте) при амплитуде смещения около 10 км на координате х = 13 км. Наложение нескольких изолиний исходного поля (рис. 7б) на результирующую карту позволяет определить положение расчетных аномалий как верное.

К сожалению, результат не лишён артефактов, связанных с несовершенством алгоритма в настоящей его реализации, в частности, на продолжении линий сдвига фиксируются ложные аномалии противоположного знака. Также небольшие ложные аномалии дает случайный шум, включенный в модель поля.

а                                           б

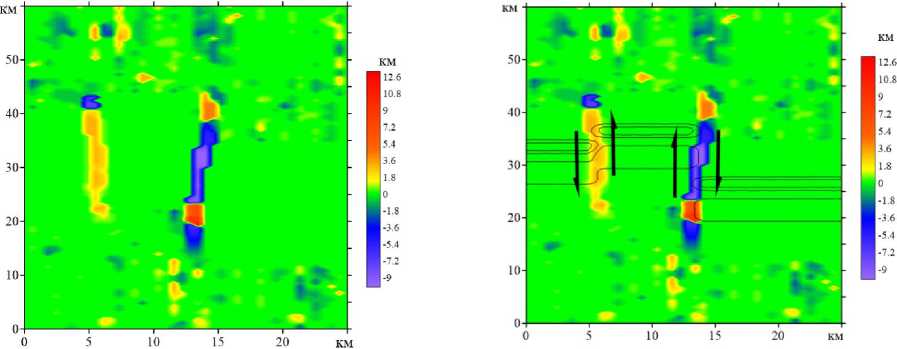
Рис. 6. Результат расчетов для синтезированной модели, представленной на рис. 3а: а – карта положения максимума ФВК, б – наложение изолиний исходного поля на карту положения максимума ФВК с элементами интерпретации

Тем не менее зона сдвига как целевая область здесь выделена, и далее алгоритм опробован на реальных данных по участку в районе хребта Колбейнси (Brandsdóttir et al., 2015). Для применения алгоритма к реальному полю и получения наиболее достоверного результата расчёт был выполнен в пяти вариантах параметров скользящих окон или расстояний между профилями (рис. 8а-д). Как оптимальный выбран вариант, представленный на рис. 8в, е с параметрами окна 20 х 10 км. Наложение изолиний исходного магнитного поля на полученную трансформацию (на рис. 8е) позволяет подтвердить, что выделенные в ходе расчетов зоны являются именно трансформными разломами со сдвиговой составляющей в кинематике. Амплитуда смещений устанавливается примерно (как 15 км), сдвиги правосторонние. Протяженность разломов, по полученным данным, небольшая – около 20–30 км.

По результату проведённой работы подтверждена эффективность предлагаемого алгоритма и внесено незначительное изменение в фрагмент тектонической схемы (рис. 9). Проявляются специфические черты трансформных разломов – их субпоперечное расположение к срединно-океаническим хребтам (СОХ) и рифтовым зонам, резкое завершение. Наиболее характерным и важным параметром сдвиговых разломов является амплитуда смещения. Если у классических сдвигов к концу происходит её затухание, то у трансформных разломов она одинакова на всем простирании. Более того, в отличие от классических сдвигов, между амплитудой смещения и длиной трансформных разломов взаимосвязи нет, в пределе амплитуда смещения может быть соизмерима с длиной трансформного разлома (Логачев, Шерман, 1981), чему полученные авторами схемы с относительно короткими трансформами не противоречат.

Необходимо отметить, что с целью проведения анализа и сравнения возможностей использования ФВК в существующем программном обеспечении с предложенной нами реализацией был произведен расчет в таких программах, как «КОСКАД 3Д» (Комплекс спектрально-корреляционного анализа данных…), «ГИС ИНТЕГРО» (Геоинформа-ционные технологии для природопользования…). Полученный в обеих программах результат не имеет аналогичной площадной визуализации, что усложняет его применение для интерпретации (Асосков и др., 2024).

Наибольшие вопросы в достоверности результатов интерпретации вызывают разломы, не пересекающие хребет и расположенные в левой части схемы (рис. 9). Предпринимая попытку описать возможный механизм формирования таких сдвигов, обратимся к истории геологического развития площади. Хребет Колбейнси сформирован при отмирании другого сегмента СрединноАтлантического хребта – хребта Эгир, располагающегося юго-восточнее, в направлении обсуждаемых сегментов, вероятно, трансформных разломов. Развитие океанического дна вдоль хребта Эгир прекратилось 25 млн лет назад, распространение океанической коры вдоль хребта Колбейнси началось примерно 10 млн лет назад (Greenhalgh, Kusznir, 2007), то есть формирование сегментов трансформных разломов, оторванных от современного СОХ, может приходиться на период перескока оси спре-динга. В таком случае мы наблюдаем сегмент отмершего и частично денудированного трансформного разлома длиной более 500 км. Данные рассуждения нуждаются в подтверждении, но позволяют не исключать полученные сегменты трансформных разломов из рассмотрения как недостоверные и не объяснимые с геологической точки зрения.

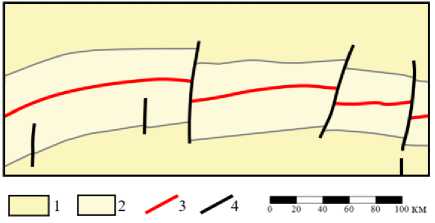
Рис. 8. Фрагмент тектонической схемы (TeMaW) с изменениями, опирающимися на расчет положения максимума ФВК, 1 – океаническая кора возраста миоцена, 2 – океаническая кора возраста плиоцена – голоцена, 3 – дивергентные границы, 4 – разрывные нарушения трансформного характера

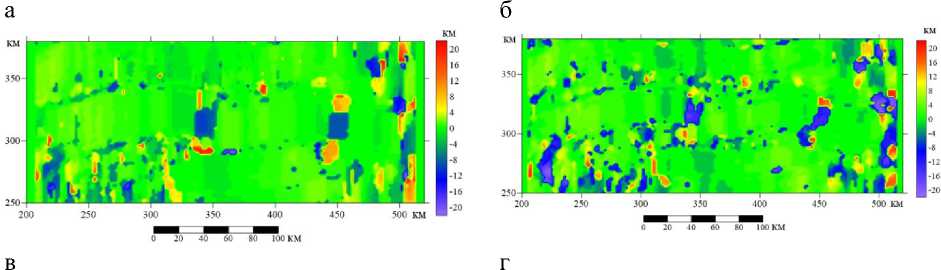
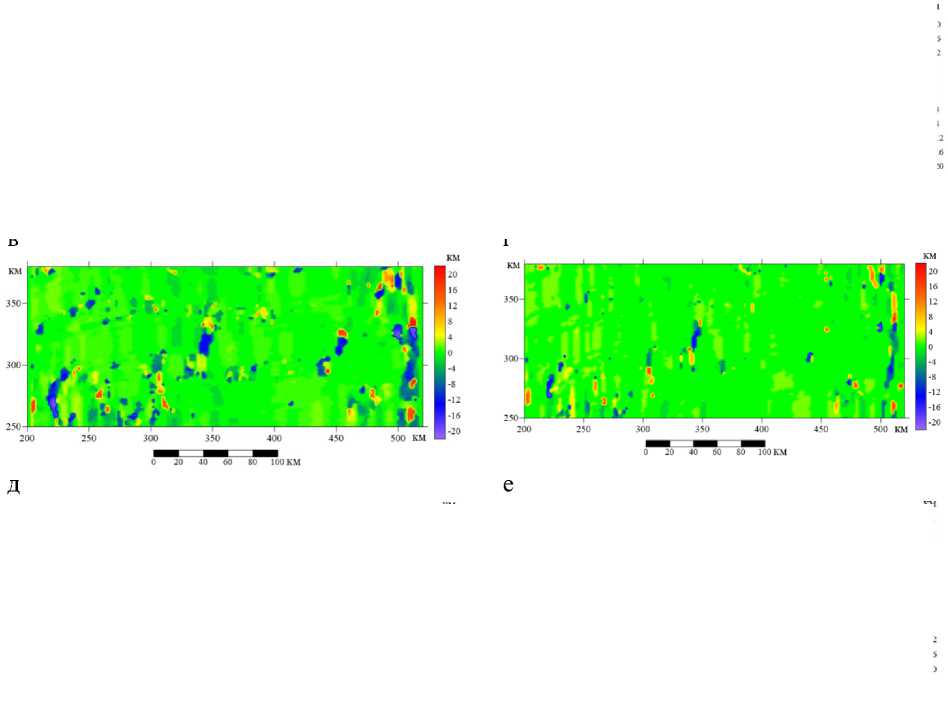
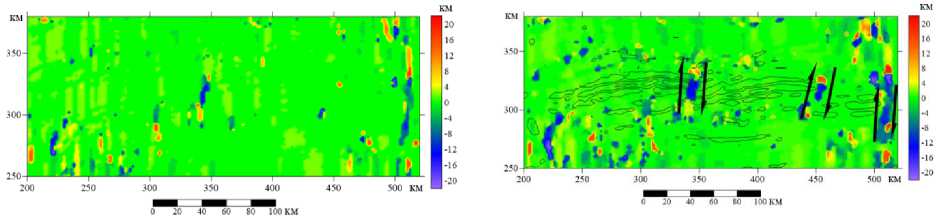
Рис. 7. Результат расчетов положения максимума ФВК для реального магнитного поля, представленного на рис. 2, при разных параметрах работы алгоритма: а – скользящее окно 32 х 18 км; б – скользящее окно 20 х 14 км; в – скользящее окно 20 х 10 км; г – скользящее окно 20 х 6 км; д – скользящее окно 32 х 6 км; е – скользящее окно 20 х 10 км с элементами интерпретации (наложены контуры исходных аномалий, стрелками показано направление основных сдвигов)

Заключение

Проведенные исследования подтверждают слабость существующих трансформаций потенциальных полей в вопросах установле- ния наличия и оценки кинематики сдвиговых дислокаций; показывают потенциал предлагаемого алгоритма расчета, использующего характеристики функции взаимной корреляции. На примере смоделированного (искусственно синтезированного) площадного распределения поля с заданными известными сдвигами установлено, что основные характеристики – направление, протяженность, амплитуда сдвига – определяются алгоритмом верно, но присутствуют артефакты, сконцентрированные на краях зон сдвига. После этого алгоритм применен к реальным данным – площадному распределению аномального магнитного поля вблизи хребта Колбейнси, где предполагается наличие трансформных разломов с кинематикой, близкой к сдвиговой. Алгоритм здесь опробован при различных параметрах работы и вычислены оптимальные условия для данной задачи – скользящее окно размером 20 х 10 км. Результирующие карты позволили подтвердить наличие сдвиговых разломов и оценить амплитуду смещений, в данном случае легко подтверждаемую визуально. Максимальное смещение определяется в размере примерно 15 км, деформация соответствует правосторонним сдвигам, но также визуализируются артефакты, которые были видны и на модельном примере, соответственно, могут быть отброшены, а алгоритм в дальнейшем должен быть улучшен для исключения таких недостатков. По результатам расчета положения максимума ФВК выделяются разрывные нарушения отличающегося строения – не пересекающие СОХ. Окончательно причина формирования таких сдвигов остается невыясненной, но предположительно может быть связана с палеоактивизацией хребта Эгир.

В будущем планируется совершенствование работы алгоритма и обработка данных по участкам с более сложным проявлением сдвиговых нарушений в физических полях. Интерес представляет также привлечение нейросетевых алгоритмов распознавания аномалий для лучшего прослеживания их корреляции, искаженной более поздними относительно формирования сдвига геологическими процессами.

Исследования выполнены в рамках подготовки диссертационной работы Асоско-ва А.Е. на соискание ученой степени кандидата наук на тему: «Трассирование сдвиговых нарушений по данным потенциальных геофизических полей с использованием взаимнокорреляционной функции».