Применение гамильтонова формализма для решения нелинейного уравнения волоконной оптики

Поле оптического импульса, распространяющегося в одномодовом волоконном световоде, поддерживающем состояние линейной поляризации, имеет вид [1].

E ( r , t ) = e x F ⁽ x , y ) A ⁽ z , t ) exp { i ( P oZ -to ot ) } ,        ⁽¹⁾

где F ( x , y ) - Гауссова функция вида exp{ - ( x 2 +y 2 )/w 2 } с радиусом моды w , A ( z , t ) – комплексная огибающая импульса, to o - несущая частота, p o = to o n ( to o )/ c - центральное волновое число.

Для огибающей оптического импульса выведено [2] уравнение

(dA n dA)   1 d2A P, d2A i + P,++

I d z    ¹ d t J 2 p o 8 z ²    2 8 1 ²                   (2)

+Ap(A|2) A = 0, названное расширенным уравнением распространения, которое существенно отличается от традиционного, называемого основным уравнением распространения [1], наличием второй производной по координате. Здесь p, = 1/ vg - величина, обратная групповой скорости, β2 – дисперсия групповой скорости, AP(| A|2) - нелинейная поправка к постоянной распространения моды в линейном приближении, которая выражается через нелинейную часть Δn показателя преломления:

ko If A n|F ( x , y ) d x d y

^Ав=                i2,

If| ^{F ( x} , y )| d x ^d y

где k_o = to _o I c .

В области прозрачности волновода Δβ является вещественной функцией. Так как β2 в области прозрачности отрицательно, то тип уравнения (2) – эллиптический. Если в уравнении (2) отбросить одну из вторых производных, то полученное уравнение параболического типа сводится к нелинейному уравнению Шрёдингера, которое является на сегодняшний день самым изученным из нелинейных уравнений, допускающих солитонные решения.

Полные уравнения второго порядка рассматривались и ранее. Так, в [3] выведено уравнение гиперболического типа для неограниченной керровской среды в упрощённой модели поля, не зависящего от поперечных координат, но затем это уравнение упрощается до нелинейного уравнения Шрёдингера. Следует упомянуть и статью [4], в которой методом секанса и tanh-методом решаются некоторые полные уравнения второго и даже третьего порядка, однако полученные решения сингулярны.

При небольших пиковых значениях интенсивности вводимого излучения нелинейную часть показателя преломления представляют степенным рядом

A n = n ₂ | E |² + n 4 | E |⁴ +—, (4) что согласно (3) приводит к степенному разложению функции Ap :

AP = y| A |² +p| A |⁴ +••• , (5)

где параметры у и р зависят от характеристик световода. При достаточно малых интенсивностях оптического поля вторым слагаемым в (5) пренебрегают.

Полученная нелинейность называется керровской и солитонное решение уравнения (2) для этого случая найдено в [5].

С ростом интенсивности вводимого излучения наблюдается [6] отклонение от керровской зависимости показателя преломления и необходимо учитывать второе слагаемое в формуле (5). Такая нелинейность называется конкурирующей (иногда этот термин применяют только в случае, если слагаемые в (5) различаются знаком).

Экспериментальные исследования в нелинейной оптике [6] подтверждают такую зависимость нелинейного показателя преломления от интенсивности оптического поля в полупроводниковых волноводах, стёклах, допированных полупроводниками, и органических полимерах. Точное солитонное решение уравнения (2) для случая конкурирующей нелинейности найдено в [7].

Целью настоящей работы является сведение уравнения (2) к нормальной системе гамильтоновых уравнений для оптической интенсивности поля импульса в случае произвольной функции нелинейного отклика среды на внешнее гармоническое возмущение. Теория гамильтоновых систем со своим мощным аппаратом производящих функций на сегодняшний день, несомненно, является самым завершённым разделом математической физики.

Основной формализм

От уравнения (2) для комплексной огибающей импульса перейдём к уравнению для оптической интенсивности I = A |2 / 2 c помощью подстановки

A ( z , t ) = 72 7 exp { i bz } ,

где b – произвольный параметр, являющийся поправкой к центральному волновому числу β 0 . Этот параметр всегда выражают через пиковое значение интенсивности или пиковое значение напряжённости.

Подстановка (6) в (2) приводит после отделения вещественной и мнимой частей полученного уравнения к следующим двум уравнениям для оптической интенсивности огибающей:

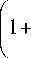
b ) d I   1 d I

I—+ p oJ 9z vs 9 t

0,

p

21S дz2

д 1

д z

b +  Ap ( I ) . 2вo          '

-^в 2

8 I ².

⁹ 2 1 Г ⁹ 1 1

д t ² (д t J

Таким образом, для одной неизвестной функции получено два уравнения. Уравнение (7) является линейным и однородным, что позволяет написать его общее решение, являющееся произвольной дифференцируемой функцией I = I ( 5 ( z , t ) ) , где

5 ( z , t ) = z - z o - vt ,                                      (9)

v = v_g (1 + b / p o ).                                    (10)

Здесь учтено, что p 1 = 1/ v_g . Иными словами, уравнение (7) определяет аргумент искомой функции, оставляя её вид произвольным. Таким образом, искомая функция представляет собой бегущую волну неизменного профиля, движущуюся с постоянной скоростью (10).

Профиль этой волны определяется уравнением (8), которое превращается в обыкновенное дифференциальное уравнение

1 -P o p 2 v ²

P o

2 1 d^ -Г d I J d 5 ² ( d 5 J

b +  Ap ( I ) . 2P o          '

8 I ².

Для дальнейшего удобства перейдём в (11) к безразмерной независимой переменной т :

т = 5

I b ( b + 2 p o ) 1 -P o p 2 v ²

Тогда уравнение (11) принимает вид

2 II - 1 ² = 4 1 ² - 8 у 1 ² Ap ( I ),                       (13)

где

Y =               .

b ( b + 2 p o )

Точкой обозначена производная по т . Как легко проверить, уравнение (13) эквивалентно нормальной системе двух гамильтоновых уравнений первого порядка:

I = 9 H / d P I ,

P,=-9H / дI,(16)

с функцией Гамильтона

H = (р;^-1) I + 2yB (I),(17)

где B ( I ) - первообразная для функции Ap ( I ), т.е.

B(I) = jAp(I)dI.(18)

Из классической механики хорошо известно, что гамильтонова система (15), (16) описывает также одномерную точечную частицу с координатой I , следовательно, уравнение (13) является также уравнением Эйлера–Лагранжа для этой одномерной механической частицы. Роль времени в классической динамике частицы играет безразмерная переменная τ, определённая формулой (12). Таким образом, гамильтонова система (15), (16), полученная для интенсивности огибающей оптического импульса, имеет ещё и механический смысл, если под I понимать не полевую функцию, а координату точки. Так как функция Гамильтона (17) не зависит явно от времени, то механическая энергия этой точки сохраняется. Хорошо известно, что решения I (τ), асимптотически стремящиеся к нулю на бесконечности, существуют (если они, конечно, существуют) при нулевой механической энергии точки. Это означает, что огибающая оптического импульса является в этом случае локализованной функцией. Именно такие локализованные решения уравнения (13) и представляют интерес. Применение механической аналогии позволяет далеко продвинуться в теории солитонов [8], [9].

Решение уравнений Гамильтона (15), (16), а следовательно, и уравнения (13) легко проводится с помощью теории канонических преобразований. Как следует из теоремы Якоби–Пуанкаре [10], если существует дважды дифференцируемая функция S ( I , p , т ), такая что |д ² S / д I д р | * 0 , то преобразование ( I , P^) ^ ( q , p ) генерируемое этой функцией:

Г , =д S / д I ; q = д S / д p ,                      (19)

является каноническим, а новая функция Гамильтона имеет вид

H(q, p, t) = H (I(q, p, t), P, (q, p, t), t) + дS(T<

+— ( I ⁽ q , p , ^{T )}, p , ^t ) .

дт

В теории канонических преобразований для двумерного фазового пространства можно исходить из четырёх типов производящих функций, зависящих от одной новой и одной старой переменной [10]. Для дальнейших целей наиболее подходящей является функция, зависящая от старого импульса и новой координаты: F = R ₂( P I , q , т ) .Тогда явный вид преобразований найдётся из разрешения уравнений

I - ⁸ F - = д P I’

dF p = г , д q а новая функция Гамильтона

^{H (} q , p , ^{t )} = H ( I ⁽ q , p , ^{t ) P} j ⁽ q , p , ^{t ) t} ) ^-

-I F ( P ⁽ q , p , ^{T )}, q , ^t ) .

дт

Будем считать в гамильтониане (17) первое слагаемое невозмущённым гамильтонианом, а второе слагаемое, обусловленное нелинейным откликом среды, – возмущением. Перейдём от динамической системы { I , P I , H } к системе { q , p , H } в представлении взаимодействия с помощью производящей функции F ( P_j , q , т ), такой, чтобы в новых переменных новая функция Гамильтона определялась бы только возмущением. Это делается с помощью производящей функции вида

F = qArthP_I - q т , (23)

которая, как легко проверить, является полным интегралом невозмущённого уравнения Гамильтона–Якоби: д F / дт = ( P_I ² - 1 ) д F / д P_I .

Из уравнений (21) следует явный вид преобразований:

I = qch2 (p + т); P, = th (p + т),(24)

а из (22) – явный вид новой функции Гамильтона:

H = 2yB(qch2 (p + t)) .(25)

Новые уравнения Гамильтона q = дH / дp; p = -дH / д q(26)

определяют динамику новых канонических переменных q и p :

ci = 4 y qch ( p + t ) sh ( p + т ) ЛР ( qch ² ( p + t )), p = - 2 y ch ² ( p + т ) ЛР ( qch ² ( p + t )).

Так как в представлении взаимодействия гамильтониан (25) зависит от времени в комбинации ( p + т ), то первый интеграл системы легко угадывается:

2 y B ( qch ²( p + т )) - q = E = 0.                   (28)

Действительно, взяв полную производную по времени от этого выражения, получим тождество с учётом (25) и (26). Механическая энергия E принята за ноль с учётом сделанного выше замечания о локализованных решениях (не путать E с энергией оптического импульса – это просто произвольная постоянная, которая в механической интерпретации имеет смысл механической энергии одномерной частицы).

Для упрощения решения динамической задачи в представлении взаимодействия разделим первое уравнение (27) на второе. В результате получим

с[ I q = - 2 pth ( p + t ).                            (29)

Заметим, что вид последнего уравнения не зависит от вида функции нелинейного отклика, а определяется только каноническим преобразованием (24), которое, в свою очередь, определяется невозмущённым гамильтонианом H o = ( P J ² - 1) I . Этот невозмущённый гамильтониан определяется в конечном итоге линейной частью уравнения (2).

Знание одного первого интеграла системы понижает её порядок на единицу, следовательно, до одного уравнения, в качестве которого удобнее всего взять уравнение (29). Вторым уравнением для решения задачи следует взять первый интеграл (28), из которого следует, что q является некоторой функцией гиперболического косинуса, зависящего от аргумента ( p+ τ). Подстановка этой функции в (29) даёт временную зависимость p (τ), что и довершает решение поставленной задачи. Так, к примеру, для керровской нелинейности B ( I ) = ц , ² реализация этой схемы даёт: p = -2т, q = 1/ 2 YЦ ch ⁴ ( т ), что является точным решением.

Заключение

Таким образом, задача нахождения локализованных решений уравнения (2) сведена с помощью теории гамильтоновых систем к двум уравнениям (28) и (29), первое из которых является алгебраическим. Примечательно, что решение представляет собой некоторую функцию гиперболического косинуса независимо от конкретного вида функции нелинейного отклика.

Автор выражает благодарность В.В. Котляру за полезное обсуждение решаемой задачи.

Работа выполнена при поддержке Министерства образования и науки РФ в рамках реализации мероприятий Программы повышения конкурентоспособности СГАУ среди ведущих мировых научно-образовательных центров на 2013–2020 годы.