Применение искусственных нейронных сетей для анализа патологий в кровеносных сосудах

Нейросетевые технологии призваны решать трудноформализуемые задачи, к которым, в частности, сводятся многие проблемы медицины. В первую очередь это связано с тем, что исследователю часто предоставлено большое количество разнородного фактического материала, для которого еще не создана математическая модель. Кроме того, необходимо представлять результаты анализа в виде, понятном специалисту прикладной области.

Одним из наиболее удобных инструментов для решения подобных задач являются искусственные нейронные сети – мощный и одновременно гибкий метод имитации процессов и явлений. Нейронные сети бывают разные по структуре и по форме, однако у них есть несколько общих черт. Основу каждой нейронной сети составляют простые элементы, называемые искусственными нейронами, которые имитируют работу нейронов головного мозга.

Отличительное свойство нейронных сетей состоит в их способности обучаться на основе экспериментальных данных предметной области. Применительно к медицинской тематике экспериментальные данные представляются в виде множества исходных признаков или параметров объекта и поставленного на основе них диагноза. Обучение нейронной сети представляет собой интерактивный процесс, в ходе которого нейронная сеть находит скрытые нелинейные зависимости между исходными параметрами и конечным диагнозом, а также оптимальную комбинацию весовых коэффициентов нейронов, соединяющих соседние слои, при которой погрешность определения класса образа стремится к минимуму [4]. В процессе обучения («с учителем») на вход нейронной сети подается последовательность исходных параметров наряду с диагнозами, которые эти параметры характеризуют. Тщательное формирование обучающей выборки определяет качество работы, а также уровень погрешности нейронной сети.

С применением нейронных сетей в практических задачах связан ряд трудностей. Одной из главных проблем применения нейросетевых технологий является заранее неизвестная степень сложности проектируемой нейронной сети, которой будет достаточно для достоверной постановки диагноза. Эта сложность может оказаться недопустимо высокой, что потребует усложнения архитектуры сетей. Известно, например, что простейшие однослойные нейронные сети способны решать только линейно разделяемые задачи [10]. Это ограничение преодолимо при использовании многослойных нейронных сетей.

В данном исследовании описывается опыт применения многослойных нейронных сетей различной архитектуры для нахождения положения и характеристик атеросклеротических бляшек в продольном срезе сонной артерии, а также анализа результатов ультразвуковой допплерографии артерий нижних конечностей.

Сравним нейросетевой подход со статистическими методами. Статистические методы (регрессионный анализ, множественная корреляция и т.д.) широко применяются в медицине при постановке диагноза. Однако реальные данные часто бывают нечеткими, с пропусками, а зависимости от входных данных могут обладать сильной нелинейностью. Все эти проблемы, включая быстрое переобучение, могут быть решены посредством применения искусственных нейронных сетей. Нейронная сеть может также уменьшить размерность пространства входных данных, оставив наиболее существенные. Тем не менее статистика и нейросетевые технологии должны не исключать, а дополнять друг друга, тем более что существует мощное программное обеспечение статистических методов.

Применение искусственных нейронных сетей для анализа результатов УЛЬТРАЗВУКОВОЙ ДОППЛЕРОГРАФИИ АРТЕРИЙ НИЖНИХ КОНЕЧНОСТЕЙ

Тяжесть ишемического синдрома нижних конечностей при окклюзионных заболеваниях брюшной аорты и ее ветвей обусловлена недостаточностью периферического кровообращения и зависит от локализации стеноза [1].

Допплеровская диагностика не только подтверждает наличие стеноза, но и определяет его локализацию и протяженность. При постановке диагноза стеноза в нижних конечностях при помощи ультразвуковой допплерографии играют роль как прямые, так и косвенные признаки [1]. Прямые признаки определяются при анализе кровотока бедренной, подколенной и задних большеберцовых вен. Косвенным критерием непроходимости глубоких вен является увеличение скорости кровотока в поверхностных венах. Только совокупная оценка обоих критериев позволяет установить точный диагноз. Все эти признаки выявляются путем сравнения кровотока в венах в симметричных точках противоположной нижней конечности.

Анализ допплеровских сигналов кровотока при обследовании артерий нижних конечностей характеризуется выявлением параметров, которые при определенном опыте дают достоверную возможность локации и дифференцирования нормальных и патологических сигналов сосуда [7].

Задача состоит в том, чтобы на основе выявленных после допплеровского сканирования параметров с некоторой степенью достоверности определить диагноз о наличии стеноза в исследуемых конечностях. Исходные данные представляются в виде табл. 1. Отсутствующие данные не играют решающей роли в постановке диагноза. Описание обозначений из табл. 1 можно найти в [9].

Для решения поставленной задачи была выбрана модель двухслойной нейронной сети прямого распространения. Нейронные сети, состоящие из двух и более слоев, имеют несколько отличительных признаков [11]:

Таблица 1

Данные допплеровского исследования нижних конечностей

Артерия	Справа		Слева
	линейная скорость кровотока	индекс пульсации	линейная скорость кровотока	индекс пульсации
Брюшная аорта	54,8	2,37	–	–
Наружная подвздошная артерия	86,5	4,85	90,2	4,49
Бедренная артерия	52,4	4,32	58,5	5,06
Подколенная артерия	51,2	5,45	47,5	4,33
Задняя большеберцовая артерия	35,3	3,0	12	2,16
Передняя большеберцовая артерия	29,4	4,55	10	1,08
Артерии тыла стопы	12,6	–	6	–
Магистральная почечная артерия	19,8	–	–	–

– каждый нейрон сети имеет нелинейную функцию активации;

– сеть содержит один или несколько скрытых слоев нейронов, которые не являются частью входа или выхода сети;

– сеть обладает высокой степенью связности.

В качестве активационной функции для нейронов сети была выбрана наиболее распространенная в многослойных персептронах нелинейная логистическая функция активации (рис. 1). Логистическая (сигмовидная) функция определяется по формуле

f < S ) = 1+TS, где S – взвешенная сумма входных сигналов нейрона.

Наличие нелинейности играет важную роль, так как в противном случае отображение «вход – выход» сети можно свести к обычному однослойному персептрону, который не способен решать нелинейные задачи [10].

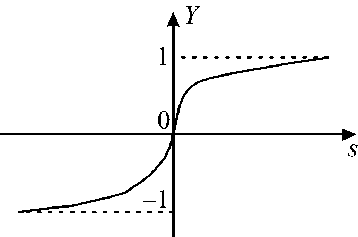
Рис. 1. Логистическия функция активации, где S – взвешенная сумма входных сигналов нейрона, Y – значение функции активации

Входной слой нейронной сети, выполняющий задачу передачи входных значений на скрытый слой, состоял из 36 нейронов, что соответствовало количеству рассматриваемых исходных параметров для постановки диагноза. Количество нейронов скрытого слоя обычно подбирается экспериментально [5]. В результате экспериментов был выбран скрытый слой, состоящий из 16 нейронов, при этом выходной слой состоял из 2 нейронов, которые соответствуют вероятностям нахождения атеросклеротической бляшки в исследуемых сосудах.

Считается, что если погрешность работы нейронной сети с данными, не участвующими в процессе обучения, находится в пределах установленной нормы, то сеть обладает хорошей обучающей способностью. Одним из факторов, определяющих способность нейронной сети к обобщению, является размер и представительность обучающей выборки. Обучающая выборка обычно формируется из примеров, каждый из которых представляет собой результат эксперимента предметной области с определенным ответом. В качестве обучающей выборки были составлены 1000 исходных параметров допплерографии кровотока с соответствующим им диагнозом, которые соответствовали реальным данным, встречающимся на практике [8].

Была обучена и протестирована нейронная сеть заданной архитектуры. Тестирование проводилось на выборке, составленной из параметров допплерографии кровотока, не участвующих при обучении нейронной сети. Погрешность определения диагноза на тестирующих данных составила ≈ 8%.

Применение искусственных нейронных сетей для нахождения положения И ХАРАКТЕРИСТИК АТЕРОСКЛЕРОТИЧЕСКИХ БЛЯШЕК В ПРОДОЛЬНОМ СРЕЗЕ СОННОЙ АРТЕРИИ

В отличие от первого подхода, в котором нейронная сеть обрабатывает числовые данные, в данном подходе происходит анализ непосредственно графического объекта, например фотографии.

Задача заключается в нахождении положения атеросклеротической бляшки на продольном срезе сонной артерии (рис. 2) [6], изображение которой получено с помощью аппарата ультразвуковой диагностики.

Нейронные сети, решающие задачи распознавания образов, требуют большого количества однотипных экземпляров, представляющих определенный класс объектов. В данном исследовании такими экземплярами выступают изображения сосудов с нарушенной проходимостью и с суженным просветом, выражающимся в наличии атеросклеротических бляшек на различных стенках сосуда, а также сосудов с ненарушенной проходимостью и нормальным состоянием просвета.

Первым шагом к решению задачи стало формирование объемной обучающей выборки, состоящей из изображений сосудов, имеющих поражение в виде атеросклеротических бляшек, и сосудов, не имеющих таких поражений. Изображения были преобразованы в модели (рис. 3) для удобства их представления в качестве входа нейронной сети. Модели сосудов, а также расположение и форма поражений согласуется с [3, 6]. Все изображения имели одинаковую размерность m×n, где m – размер изображения по горизонтали, а n – по вертикали.

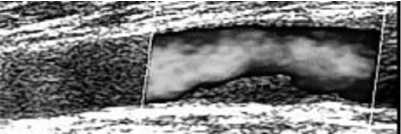
Рис. 2. Изображение атеросклеротической бляшки в сонной артерии

Рис. 3. Пример модели артерии с атеросклеротической бляшкой

Существуют несколько способов представления исходного изображения в качестве входной последовательности нейронной сети:

– изображение размерности n × m записывается в виде вектора m∙n ;

– осуществляется дополнительная обработка изображения с целью фиксации наиболее информативных участков и преобразования их в некоторый массив чисел.

Наибольшее распространение получил первый способ, его достоинство заключается в том, что он не требует дополнительной обработки изображения, что в некоторых случаях может превратиться в достаточно емкую задачу [10]. Однако недостаток этого метода заключается в том, что для формирования таких векторов необходимо большое количество памяти, а скорость обучения нейронной сети существенно падает. Для решения поставленной задачи был выбран второй способ представления изображения в качестве входного вектора нейронной сети. Наиболее информативными участками изображения в данном случае являлись такие показатели, как геометрия сосуда, проходимость, толщина стенок, диаметр и состояние просвета. В результате обучающая выборка была получена с использованием формулы

l

V = UVi, i=1

где l – количество входных образов, V i – входной вектор i -го образа, V – обучающая выборка.

Выходом нейронной сети, или результатом ее работы, считались координаты расположения стеноза на модельном изображении сосуда. Если стеноз не наблюдался, то возвращалась последовательность, сигнализирующая об этом.

В качестве архитектуры нейронной сети была выбрана модель двухслойной нейронной сети прямого распространения. Размерность входного слоя нейронной сети соответствовала размерности входного вектора и была равна 3600 нейронам. В результате экспериментов с количеством нейронов в скрытом слое была замечена следующая тенденция:

– при использовании скрытого слоя, состоящего из 1200 нейронов и менее, процесс обучения замедляется пропорционально снижению количества нейронов, а ошибка обучения увеличивается;

– при использовании скрытого слоя, состоящего из более чем 1200 нейронов, процесс обучения выполнялся за меньшее время, но в связи с усложнением архитектуры сети ей требовалось производить больше вычислительных операций, что также снижало скорость обучения, а ошибка обучения практически перестала снижаться.

В качестве оптимального был выбран скрытый слой, состоящий из 1200 нейронов. Размерность выходного слоя определялась также 1200 нейронов. В качестве функции активации для нейронов сети была выбрана логистическая нелинейная функция (см. рис. 1). Общая архитектура нейронной сети приведена на рис. 4. Подробное описание обозначений, используемых на рис. 4, находится в [5].

Таблица 2

Погрешности работы нейронной сети

№ п/п	Y i	Y exp	Погрешность, %
1	2,177	2	8,85
2	2,203	2,05	7,5
3	2,28	2,11	8,1
4	2,18	2,92	8,9
5	2,619	2,44	7,34
6	2,66	2,5	6,4
7	2,69	2,5	7,85
8	2,9	2,7	7,64
9	2,63	2,42	8,7

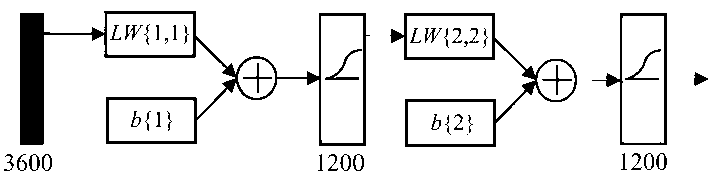
Рис. 4. Архитектура нейронной сети, где b { i } – вектор смещения i -го слоя,

LW { i, j } – матрица весов от слоя i к слою j

Нейронная сеть обучалась на выборке, состоящей из 500 изображений сосудов, в которых наблюдался стеноз, а также из сосудов, в которых его не было. Обучение нейронной сети производилось одним из наиболее популярных алгоритмов для обучения многослойных нейронных сетей – алгоритмом обратного распространения ошибки [7]. Этот алгоритм основывается на коррекции ошибок, когда синоптические веса настраиваются с целью максимального приближения выходного сигнала сети к желаемому в статистическом смысле [7]. Обучение продолжалось в течение 500 эпох, после чего уровень ошибки достиг минимального значения и обучение было остановлено [2].

Тестирование обученной нейронной сети проводилось на тестирующей выборке, состоящей из 100 элементов. Погрешность работы нейронной сети на тестирующих данных высчитывалась по формуле

S i =

exp Y_i

-

Y i

exp Y_i

100% ,

где S i – погрешность i -го результата, n – количество тестирующих данных, i – числа 1, n , Y i – результат работы нейронной сети, Y i ^exp – ожидаемый результат.

В результате тестирования были получены погрешности, некоторые из которых представлены в табл. 2. Полученные данные показывают, что погрешность работы обученной нейронной сети над тестовыми данными, состоящими из изображений сосудов со стенозом и без стеноза, находится в пределах 9%, и это означает, что нейронная сеть научилась обобщать информацию и способна эффективно определять локацию стеноза в моделях сосуда.

Выводы

В данной работе были рассмотрены два различных способа применения искусственных нейронных сетей для анализа патологий в сосудах. В одном из подходов нейронная сеть работала с исходными параметрами для определения диагноза, которые представлялись в виде набора чисел, другой подход предполагал использование непосредственно графического изображения сосуда. В обоих случаях были построены нейронные сети одинаковой топологии, но различающиеся количеством нейронов, задействованных в различных слоях нейронной сети. Результаты обучения и проверки работоспособности спроектированных нейронных сетей показывает их успешное применение для решения поставленных задач и способность находить сложные закономерности и взаимосвязи между различными объектами, относящимися к одному классу данных. Также можно предположить, что при использовании более ёмких и разнообразных обучающих выборок погрешности работы нейронных сетей будут уменьшаться. После того как сеть обучена, она становится надежным и недорогим инструментом анализа патологий в кровеносных сосудах.