Применение итерационно-интерполяционного метода для решения задач математической физики
Автор: Гришин Анатолий Михайлович, Зинченко Владислав Иванович, Ефимов Константин Николаевич, Якимов Анатолий Степанович
Журнал: Вычислительная механика сплошных сред @journal-icmm
Статья в выпуске: 3 т.1, 2008 года.
Бесплатный доступ
На основе итерационно-интерполяционного метода разработан алгоритм решения уравнения параболического типа и получена разностная схема для численного решения уравнения вида пограничного слоя с учетом различных режимов течения и в широком диапазоне чисел Рейнольдса и Маха. Полученная неявная разностная схема безусловно устойчивая с погрешностью аппроксимации второго порядка по поперечной и первого порядка по маршевой переменной. Методом пробной функции рассмотрена практическая сходимость разностной схемы.
Короткий адрес: https://sciup.org/14320437
IDR: 14320437
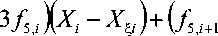
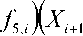
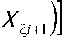
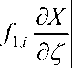
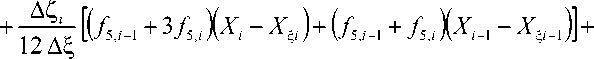
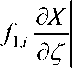
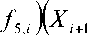
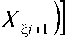
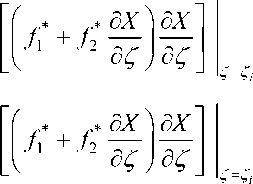
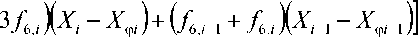
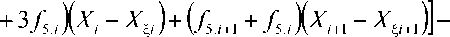
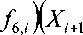
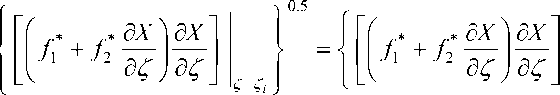
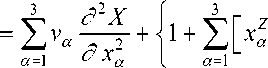
Список литературы Применение итерационно-интерполяционного метода для решения задач математической физики
- Гришин А.М. Об одном видоизменении метода М. Е. Швеца//Инженерно-физический журнал. -1970. -Т. -19, № 1. -С. 84-93.
- Гришин А.М., Берцун В.Н. Итерационно-интерполяционный метод и теория сплайнов//ДАН СССР. -1974. -Т. 214, № 4. -С. 701-704.
- Grishin A M., Bercun V N. The Iterational-Interpolation Method and Spline Theory//Soviet. Math. Dokl. -1974. -V. 15, N. 1. -P. 222-227.
- Гришин А.М. Об одном итерационно-интерполяционном методе//Труды НИИ Прикладной математики и механики при ТГУ. -Томск: Изд-во ТГУ, 1973. -С. 45-48.
- Гришин А.М., Якимов А.C. Обобщение итерационно-интерполяционного метода для решения трехмерного параболического уравнения общего вида//Вычислительные технологии. -1999. -Т. 4, № 2. -С. 26-41.
- Якимов А.С. Об одном методе расщепления//Численные методы механики сплошной cреды. -1985. -Т. 16, № 2. -С. 144-161.
- Гришин А.М., Зинченко В.И., Ефимов К.Н. Субботин А.Н., Якимов А.С. Итерационно-интерполяционный метод и его приложения. -Томск: Изд-во ТГУ, 2004. -320с.
- Войнович П.А., Жмакин А.И., Попов Ф.Д., Фурсенко А.А. Численное исследование течений газа с разрывами сложных конфигураций//Журнал вычисл. матем. и матем. физики. -1979. -Т. 19, № 2. -C. 1608-1614.
- Яненко Н.Н. Метод дробных шагов решения многомерных задач математической физики. -Новосибирск: Наука, 1967. -195 с.
- Зинченко В.И., Ефимов К.Н., Якимов А.С. Исследование характеристик сопряженного тепло-и массообмена при вдуве газа и термохимическом разрушении обтекаемого тела//Теплофизика высоких темпера-тур. -2007. -№ 4. -С. 749-755.
